La
nouvelle Algèbre
de l'Infini
--> Le
nombre supérieur à lui-même, inférieur à lui-même, et égal
à lui-même
--> "Quel
nombre ajouté à lui-même donne lui-même ?"
--> L'Infini
et l'Algèbre du Cycle
Documents associés :
La
Loi de l'Alternation Zéro
La
Loi de l'Alpha et de l'Oméga
L'Algèbre
universel des ensembles
La
nouvelle Science des nombres
L'Algèbre
du Cycle (vidéo)
Toute
la lumière sur les Paradoxes (vidéo)
La
nouvelle Algèbre
de l'Infini
Le
nombre supérieur à lui-même, inférieur à lui-même, et
égal à lui-même !
Considérons
cinq ensembles et leurs éléments, donnés par le tableau suivant
:
La
logique qui permet de dire que deux ensembles ont le même nombre
d'éléments est très simple, elle s'appelle techniquement la bijection entre
les deux ensembles. Cela signifie qu'en associant
deux à deux (et coup pour coup) les éléments des deux ensembles,
on les termine en même
temps, ou on ne termine jamais l'un avant l'autre. Autrement
dit, dans cette association, il n'arrive jamais que l'on ait
épuisé les éléments d'un des ensembles, alors qu'il en reste
au moins un chez l'autre. S'il cela ne peut arriver, alors
on dit qu'il y a une bijection entre les deux
ensembles, ce qui signifie qu'ils ont un même nombre d'éléments.
Par
exemple, dans le tableau ci-dessus, les ensembles A et E ont
le même nombre d'éléments, car en les associant, Terre avec
Pierre, Lune avec Pauline, Soleil avec Jacques, etc., quand
on termine à Jupiter avec l'ensemble A,
on termine aussi à Bruno avec l'ensemble E.
On les finit en même temps, ou en tout cas on ne finit jamais
l'un avant l'autre. Il y a donc une bijection entre A et E,
ce qui veut dire qu'ils ont exactement un même nombre d'éléments,
ici 6.
En
revanche, quand on essaie de faire une bijection entre A et B,
tout va bien jusqu'à ce qu'on arrive au terminus de A avec Jupiter;
à cet élément correspond l'élément 90 chez B;
mais
B n'aura pas dit son dernier mot, car il se
poursuit avec l'élément 45. Il
n'y a donc pas bijection entre A et B,
et dans ce cas B a plus d'éléments que A,
ici 7. Et il y a une bijection entre B et D,
qui abattent leurs dernières cartes en même temps, l'élément
45 pour B et Nevers pour D.
Et
quand à l'ensemble C, il n'est en
bijection avec personne dans le tableau, il peut encore jouer
deux coups par rapport à B ou D,
il essaie de tenir tête à tête avant de jeter à son tour l'éponge
après son dernier élément qui est la Prune, s'inclinant devant
N qui avec ses "Trois points de suspension"
("...")
après l'élément 8, annonce clairement son intention de poursuivre
indéfiniment. Au tableau des scores (le "nombre d'éléments"),
il l'arbitre inscrit le symbole de l'infini "
".
Mais quand il s'agit de l'ensemble des nombres naturels : 0,
1, 2, 3, 4, 5, 6, 7, 8, ...., le nombre total des éléments
est un nombre infini nommé Aleph zéro, couramment appelé Oméga et
noté de la dernière lettre minuscule de l'aplhabet grec : 
;
mais pour des raisons pratiques on le notera ici W.
C'est donc le nombre des éléments de l'ensemble des entiers
nturels N.
Et
maintenant considérons les trois ensembles P, I et N du tableau
suivant :
Ici,
N va pouvoir se mesurer à des adversaires
de son gabarit. Comme chacun le sait, l'ensemble des entiers
naturels 0,
1, 2, 3, 4, 5, 6, 7, 8, .... comprend le sous-ensemble P des
nombres pairs : 0, 2, 4, 6, 8, 10, 12, ...,
et le sous ensemble I des nombres impairs :
1, 3, 5, 7, 9, 11, 13, .... Les trois ensembles comportent
une infinité d'éléments. Et N a
raison de dire : "Mes adversaires P et I ont
exactement le même nombre d'élements, qui est donc la moitié
du nombre de mes éléments, puisque je totalise les deux. Donc
au match de la bijection, chacun déclarera
logiquement forfait à mi-chemin. Quand P aura
joué tous ses nombres pairs, moi il me restera tous les nombres
impairs qu'il
ne possède pas. Et quand I aura joué tous ses nombres impairs,
moi il me restera tous les nombre pairs qu'il ne possède pas.
Au score final, il afficheront donc la motié de mes points,
à savoir W/2, tandis que moi j'afficherai
W."
N a-t-il
raison de dire cela ? Dans la logique actuelle, la Logique
Négative (une logique du "Tout OU Rien",
"Vrai OU Faux"), la réponse doit obligatoirement être SOIT
Oui, SOIT Non, mais
pas les deux ! Dans cette logique, N ne peut
pas à la fois avoir raison et avoir
tort, son propos ne peut pas à la fois être Vrai et Faux.
Mais
cette logique n'est pas logique de l'Univers
TOTAL, ce n'est pas la logique de l'Infini.
Dans cette logique, toute chose est vraie, et le contraire
de toute chose est vrai aussi, sans pour autant qu'il y ait
contradiction ou paradoxe ! La situation est simplement comme
les phrases "Il pleut dans l'Univers" et "Il
ne pleut pas dans l'Univers". Les deux sont vraies, car
il pleut toujours quelque part dans l'Univers TOTAL, et ailleurs
il ne pleut pas dans le même Univers. Cela dépend du contexte,
de quel point de vue on se place. Pour l'un "Il pleut est vrai",
car chez lui il pleut; et pour l'autre, c'est le contraire
qui est vrai.
Dans
ce problème de l'Infini, ça dépend simplement de quel raisonnement
on fait, de la manière dont on organise les nombres de N par
exemple, de la "stratégie" de N pour
épuiser ses aversaires avec lui, ou de leurs "stratégie"
pour lui resister avec leur effectif moindre. Si par exemple
N dispose ses éléments ainsi : 0, 2, 4, 6,
8, 10, 12, ..., 1, 3, 5, 7, 9, 11, 13, ...., ne jouant donc
que sa moitié contre ses adversaires, il les épuisera avec
cette moitié, et il lui restera l'autre moitié. Face à cela
ceux-ci ont une très simple riposte : organiser leurs éléments
exactement de la même manière, le miracle de l'Infini le leur
permet. Par exemple, P peut diviser lui aussi
son effectif de cette façon : 0, 4, 8, 12, 16, ...., 2, 6,
10, 14, 18, ..... Le secret est très simple, il réside en ces
très importants "Trois points de suspension" ("...").
Chaque fois que l'on en rencontre, cela signifie que l'Infini
s'est dédoublé ! Et l'Infini peut se dédoubler une infinité
de fois ! Il suffit donc à chaque fois de veiller à opposer
à l'adversaire le même nombre de dédoublements, ce qui signifie
simplement qu'on organise ses éléments exactement de la même
manière que lui. Alors pour chaque élément qu'il jouera, on
aura toujours chez soi un élément correspondant pour lui répondre,
coup pour coup !
Dans
un match de bijection entre deux infinis (du moment où il s'agit
de l'infini !), quelle que soit la
différence apparente au départ, on a les trois possibilités
: "match nul",
"victoire",
'défaite". L'Infini est la chose par excellence qui est à
la fois égale à elle-même, supérieure à elle-même, et inférieure
à elle-même. L'Infini gagne contre lui-même, et perd contre
lui-même.
Dans
le problème qui nous concerne, N a
donc raison de dire qu'il a plus d'éléments que ses adversaires,
mais finalement, les trois ensembles ont exactement le même
nombre d'éléments. Dans le cas de figure du tableau précédent,
les trois ensembles ont la même organisation, le même nombre
d'exemplaires de l'infini de base, à savoir
Oméga ou W. Cela se traduit dans le
tableau par le fait que chacun le même nombre de "Trois
points de suspension" ("..."),
à savoir 1 pour chacun. Donc ici, "match nul" ! Les trois ont
donc exactement le même nombre d'élements (W ou
Oméga ou encore Aleph zéro),
et on découvre une très importante loi de l'Infini : W
+ W = W ! Et ceci (écrit dans le sens W
= W + W) traduit
tout simplement la propriété de duplication de
l'Univers
TOTAL U, à savoir : U
= U + U. Cette propriété est étroitement liée à sa
propriété d'Auto-appartenance, à sa structure
fractale.
"Quel
nombre ajouté à lui-même donne lui-même
?"
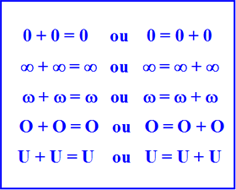
Quel nombre ajouté à lui-même
donne lui-même ?
Autrement dit, quelle est la solution de l'équation : X + X =
X ?
L'actuelle algèbre des nombres réels ne connaît que Zéro comme
solution.
Elle ignore l'autre solution, l'Infini, qui est orpheline dans
une autre algèbre, celle des cardinaux infinis.
Mais désormais on a les deux solutions dans l'Algèbre
universelle.
Les deux solutions sont une seule et même chose : l'Univers
TOTAL,
qui est à la fois le Vide
et le Plein.
"Quel
nombre ajouté à lui-même donne lui-même ?"
Il s'agit donc de résoudre l'équation : X
+ X = X, et on trouve
en calculant le plus normalement du monde : X = X -
X, d'où
X = 0. On conclut habituellement que l'unique
solution est 0. Mais erreur !
Car
le paradigme scientifique actuel (et en particulier algébrique)
utilise toutes sortes d'objets métamathématiques pour résoudre
ses problèmes, comme par exemple la notion de variable X.
Elle n'a pas de statut mathématique explicite, elle est extérieure
à la mathématique, une lettre utlisée pour représenter un nombre,
mais dont le statut numérique n'est pas défini. C'est pourquoi,
quand on aboutit à la conclusion : X = 0,
on ne voit comme seule solution que 0, mais
pas la seconde solution qu'est X lui-même
! Mais il suffit de considérer le résultat obtenu précédemment,
W + W = W, de calculer de la même façon avec
W, pour aboutir à la conclusion : W
= 0. Et là on voit clairement deux solutions à la
question, 0 et W, c'est-à-dire
donc le Zéro et l'Infini !
Et du coup, la vraie nature de la notion de variable saute
aux yeux, c'est la même notion que celle d'Infini.
La notion de variable a désormais un statut mathématique explicite,
et non plus métamathématique.
L'Infini
et l'Algèbre du Cycle
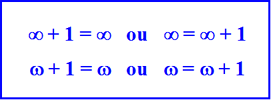
"Quel
nombre reste égal à lui-même, qu'on lui ajoute 1 ou qu'on lui
retranche 1 ?"
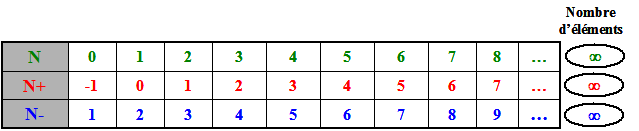
Ici,
l'ensemble N+ compte un élément de plus que N,
à savoir l'élément -1)
Et N- compte un élément de moins que N,
car il lui manque le 0. Il lui manque donc
deux éléments de moins que N+;
à savoir -1 et 0.
Et pourtant, comme expliqué plus haut, les trois ensembles
ont exactement le même nombre d'éléments, à savoir W,
car il existe une parfaitement bijection entre les trois. On
a donc tout simplement les égalités suivantes : W
= W + 1 et W = W - 1.
De
W = W + 1 on déduit (si on cacule le plus
normalement du monde) : W - W = 1, d'où : 0
= 1. On découvre que cette propriété de l'Infini d'être
égal à lui-même si on lui ajoute (ou si on lui retranche 1)
s'exprime par une simple et étonnante égalité : 0
= 1 ! Le genre d'égalités que la
science actuelle qualifie d'absurde même !
La
pire chose qui puisse arriver à la science
(et c'est arrivé !)
est de dire quelque chose qui revient à nier l'existence de
l'Univers (au sens le plus TOTAL du
terme) ! C'est le cas si la science appelle
un "paradoxe" ou
une "contradiction" (c'est-à-dire
donc quelque chose faux, d'impossible ou
d'absurde) une propriété fondamentale
de l'Univers
TOTAL, une des lois les plus
fondamentales de la Réalité TOTALE.
Cette loi porte sur le Zéro et
l'Infini (ou
sur le Vide et sur le Plein). Nier
cette loi de Univers
TOTAL (donc
cet Univers) est dans le meilleur des cas la plus
grosse erreur scientifique que l'homme ait jamais
faite(due
au fait de fonctionner
avec le paradigme de la Négation),
et dans le pire des cas c'est faire une science qui
est tout simplement
le plus
grand
chef-d'oeuvre de Négationnisme de
tous les temps !
Un
des grands problèmes des mathématiques et des sciences actuelles
est de pratiquer beaucoup le "Deux lois, deux mesures",
l'équivalent scientifique de l'insupportable "Deux
poids, deux mesures". Cela consiste très souvent à établir
des lois fondamentales pour une certaine catégories d'objets,
puis à refuser ces mêmes lois pour une certaine partie de la
catégorie, à faire des incessantes exceptions à la règle (ce
qui revient à faire de la Ségrégation une
méthode scientifique !), tout cela au nom d'une philosophie
scientifique très douteueuse, qui est tout simplement le paradigme
de la Négation.
Par
exemple, on établit des lois fondamentales de l'arithmétique
(ou de l'algèbre) pour les nombres entiers naturels ou réels,
et ces lois ne sont plus valables pour les nombres infinis,
parce qu'on ne veut pas aboutir à des relations comme 0
= 1,
Zéro = Infini, que l'on considère A
PRIORI comme absurdes, comme ne pouvant traduire aucune
vérité scientifique !
Pour
les mêmes raisons, on dit par exemple que l'on peut diviser
par tout nombre réél sauf par le 0 !
On interdit de diviser simplement 1 / 0 pour
trouver l'Infini W,
et donc naturellement de diviser 1 / W pour
trouver 0. On ne veut donc pas que l'on dise
:
1 / 0 = W, et 1 / W = 0, et
de faire participer cet Oméga (ou W)
aux calculs, exactement de la même manière que tous les autres
nombres. En effet, le faire, aboutirait très rapidement à des
égalités du genre : 0 = 1, Zéro
= Infini, 2 = 1, 77 = 20,
etc., une
catastrophe logique ou mathématique pense-t-on.
Mais catastrophe, ou bien on ne sait pas tout simplement à quelle
logique obéit ce genre d'égalités ?
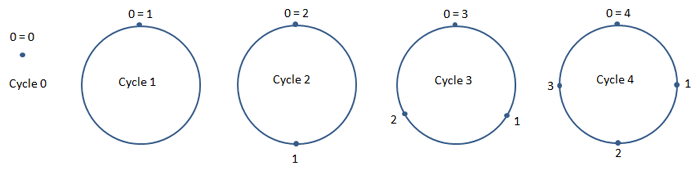
Les égalités de
la forme 0 = 0, 1 = 1, 2 = 2, X = X, etc., sont celles du Cycle
0;
la science actuelle fonctionne seulement avec ce type d'égalité,
mais elle n'est seulement qu'un cas très particulier dans l'infinité de
types d'égalité qui existent dans l'Univers
TOTAL !
Les égalités de
type : 0 = 1 ou 1 = 0, 1 = 2 ou 2 = 1, 72 = 73 ou 73 = 72, X = X + 1 ou X +
1 = X, etc., sont celles du Cycle 1;
avec ce type d'égalité de la forme générale X
= Y commence
la "Terra Incognita" ("Terre Inconnue") ou "Universum
Incognita" ("Univers
Inconnu") pour la science actuelle,
toute l'immensité actuellement inconnue de l'Univers
TOTAL, que
le Fils
de l'homme révèle aujourd'hui.
Ce n'est pas parce que l'on ne connaît pas une chose, ou que l'on ne comprend
pas son utilité dans l'Univers
TOTAL, qu'elle
est "absurde"...
Depuis
l'école primaire donc, on apprend aux enfants à faire ces
opérations
élémenatires
(addition,
soustraction,
multiplication)
avec comme par exemple premier opérande 1 et second opérande
0 :
1
+ 0 = 1 ;
1 - 0 = 1;
1 x 0 = 0;
1 / 0 = ... ?
Pour
la quatrième opération, mystère ! On s'empresserait de "corriger"
un élève qui très naturellement et sans trop réfléchir écrirait
: 1 / 0 = 0 ou 1 / 0 = 1 (voir
dans le document Où est
la frontière de la Science ? l'expérience
de l'ancien prof de maths qu'était le Fils
de l'homme en lycée
professionnel en France). Pourquoi donc 1 / 0 n'aurait pas
le droit d'avoir comme résulat un nombre réel,
exactement comme 1 + 0 = 1, 1 - 0
= 1, 1 x 0 = 0 ? Et pourquoi le résultat
fondamental ne serait-il pas 1 / 0 = 0, exactement
comme pour l'opération associée la multiplication : 1
x 0 = 0 ? Cette réponse est très fortement suggérée,
car pour les deux opérations associées (l'addition et la soustration),
la réponse est la même, à savoir 1.
En
tout cas est-il que l'égalité 1 / 0 =
0 dit
tout simplement ceci : Infini = Zéro ou Zéro
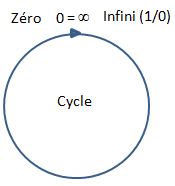
= Infini. Ce résultat traduit tout simplement le Cycle,
à savoir que les nombres ne doivent pas être conçus
comme des objets d'une Droite numérique (avec le Zéro à un
bout et l'Infini de l'autre), mais comme les objets d'un
Cercle numérique, avec le Zéro et l'Infini qui se rejoignent
(Zéro
= Infini). Il s'agit alors du Cycle Infini,
exactement comme pour le Cycle 3.
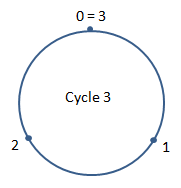
Chaque
Cycle a son algèbre. Par exemple, le Cycle
3 a son algèbre, très facile. L'égalité caractéristique (ou
canonique) de ce Cycle est : 0 = 3. Dans ce
Cycle, les calculs 1 + 0 ou 1 + 1 se font comme normalement
(c'est-à-dire comme dans le Cycle Infini) : 1 + 0 = 1, et 1
+ 1 = 2. Mais on a : 1 + 2 = 0, puisque 0 = 3. Et 2 x 2 = 1,
puisque 2 x 2 = 4 dans le Cycle Infini, mais que 4 = 1 parce
que 3 = 0; c'est-à-dire (3 = 0 donc, 3 + 1 = 0 + 1; donc 4
= 1). Dans le Cycle 3, on a 1 / 0 = 3, et aussi 1 / 0 = 0,
puique dans ce cycle 0 = 3. Pour les mêmes raisons, dans ce
cycle, 1 / 3 = 0.
De
même, dans le Cycle 70 par exemple, 24 + 40 se calcule normalement,
comme dans le Cycle Infini. On a : 24 + 40 = 64. Mais 33 +
39 = 2, car 33 + 30 = 72 dans le Cycle Infini, et 72 = 2, car
70 = 0 pour le Cycle 70. Dans ce cycle, 1 / 0 = 70 = 0, et
1 / 70 = 0 = 70.
Bref,
dans le Cycle X, le nombre X joue le rôle de l'Infini, on a
donc 1 / 0 = X = 0, et 1 / X = 0
= X. Et on constate que le raisonnement est le même pour
le Cycle W. Car 1 / 0 = W = 0, et 1 / W = 0 = W. Dans le paradigme
du Cycle, les notion de variable (ici X) et d'infini (ici W)
sont tout simplement la seule et même notion.
ubertElie
