Sommaire de cette page :
- Ontologie de Identité ou de Négation, et Ontologie l'Equivalence ou d'Alternation.
L'Equivalence, l'Egalité large, universelle, la bonne conception de l'Egalité!
- La conception actuelle de l'Egalité, de l'Equivalence et des Classes d'Equivalence:
le paradigme de l'Identité, de la Séparation, de la Négation absolue, du Déni de l'Univers TOTAL
- La nouvelle conception de l'Egalité, de l'Equivalence et des Classes d'Equivalence:
le paradigme de l'Equivalence, de l'Union, de l'Alternation, de l'Univers TOTAL
- Résumé technique
- Voir aussi
Ontologie de Identité ou de Négation, et Ontologie l'Equivalence ou d'Alternation.
L'Equivalence, l'Egalité large, universelle, la bonne conception de l'Egalité!
Sommaire du sous-titre
L'Equivalence ou le "Différent et pourtant Même": la très générale et très puissante notion d'Egalité de l'Univers TOTAL
Découvrez en vidéo l'Equivalence, la nouvelle conception de l'Egalité

La Loi du XERY ou "X ER Y" ou "X EST Y" ou "X = Y", la Loi de l'Equivalence Universelle,
qui dit que toutes choses X et Y, quelles que soient leurs différences apparentes (la différence est juste nécessaire pour la Diversité),
sont fondamentalement une seule et même chose, à savoir l'Univers TOTAL, l'Univers-DIEU, l'Alpha et l'Oméga.
Autrement dit, il EST TOUT et absolusment TOUT, il EST chaque chose et chaque être, il est donc X et Y.
Ceci signifie que la notion d'égalité de l'Univers TOTAL n'est pas l'actuelle égalité, à savoir l'identité, celle de ce monde de Négation,
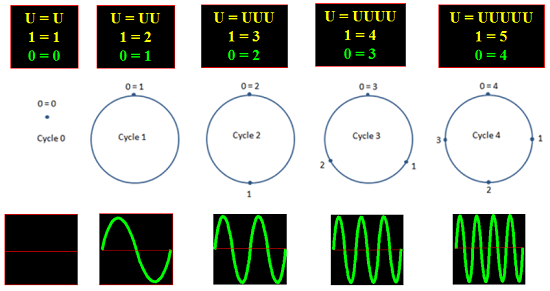
égalité avec laquelle on dit seulement 0 = 0, 1 = 1, X = X, Y = Y,
donc 4 = 4 ou 2 + 2 = 4.
L'identité est une égalité restreinte, dont le but est seulement justement d'exprimer les identités,
de dire que Théophile est Théophile, que Angélique est Angélique,
bref que chacun ou chaque chose a sa propre identité, elle est identique à elle-même.
Cette égalité (l'identité) est juste un cas particulier d'une égalité plus générale, à savoir
l'équivalence,
avec laquelle on dit aussi 0 = 1, 4 = 5 ou 2 + 2 = 5, et plus généralement: X = Y.
L'Equivalence Universelle ou XERY,
qui est une autre manière d'exprimer le Théorème de l'Existence,
est la Loi fondamentale de l'Univers TOTAL,
c'est la Loi de l'Union, de l'Unité, et par conséquent la Loi même de l'Amour, la Loi des Anges, la Loi de Dieu.
Le but du présent document est de vous permettre de comprendre techniquement l'identité et l'équivalence,
ainsi que les logiques qui leur sont respectivement associées, la Négation et l'Alternation (ou Affirmation).
L'Identité: l'actuelle de l'Egalité. L'Equivalence: la nouvelle conception de l'Equivalence

La chose X est identique à elle-même, de même que Y est identique à elle-même,
chacune à sa propre identité qui la distingue de l'autre, et des autres choses en général.
On écrit X == X et Y == Y, pour dire que chaque chose n'est identique qu'à elle-même.
X et Y ne sont donc pas égaux au sens de l'Identité.
L'Identité est appelée l'Egalité stricte ou restreinte,
et son contraire est appelé la Distinction.
On écrit: X ≠≠ Y pour dire que X et Y
ne sont pas identiques mais distincts.
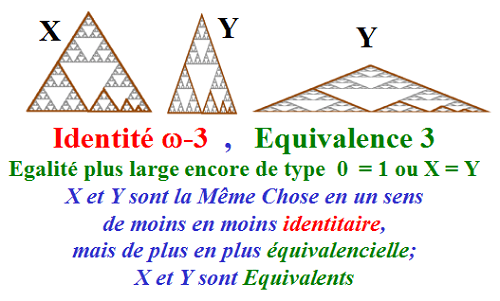
Cependant, X et Y sont deux modèles du seul et même Triangle de Sierpinski.
On dit qu'ils ils sont égaux ou équivalents de ce point de vue.
On écrit pour cela: X = Y, la nouvelle conception de l'Egalité, appelée l'Egalité large.
X et Y sont différents du point de vue de la taille,
mais aussi du fait que X est à l'intérieur de Y et que Y n'est pas à l'intérieur de X.
Ce sont toutes ces différences qui sont à l'origine de leur distinction,
car dès qu'il existe la moindre différence entre deux choses, alors elles sont obligatoirement distinctes!
Et à l'inverse deux choses distinctes sont obligatoirement différentes du point de vue de l'Identité.
Mais ni la distinction, ni la différence ne les empêchent d'être équivalentes à un certain point de vue,
comme par exemple ici d'être deux modèles du même Triangle de Sierpinski.
On écrit X ≠ Y pour signifier que X et Y sont différents,
mais alors, comme pour l'Equivalence, il faut préciser de quel point de vue ils sont différents.
C'est toujours une contradiction de dire que deux choses distinctes sont identiques,
mais ce n'est pas une contradiction de dire que deux choses différentes sont équivalentes,
car elles sont toujours équivalentes d'un certain point de vue,
et le cas échéant elles sont équivalentes du point de vue de leur qualité commune
de CHOSE,
de leur appartenance commune à Univers TOTAL, l'Ensemble de toutes les choses.
Autrement dit, deux choses obéissent obligatoirement
au modèle Chose,
le modèle le plus fondamental.
Deux choses ne peuvent donc pas être différentes à tous les points de vue
à cause de cette très importante Equivalence fondamentale,
celle associée au modèle Chose,
celle de l'Univers TOTAL.
La notion d'Egalité est l'une des plus fondamentales de la pensée,
elle est d'une extrême importance, car elle est tout simplement la notion
d'ETRE,
elle est un simple synonyme du verbe ETRE;
c'est une notion ontologique.
En effet, quand nous disons "X = X" ou "X = Y",
nous disons simplement:"X EST X" ou "X EST Y".
C'est donc une notion très fondamentale en science. Et pourtant, c'est l'une des plus mal conçues!
Non seulement cela, la science actuelle fonctionne avec une mauvaise notion d'Egalité: l'Identité.
C'est le fait de dire seulement des choses du genre: "0 = 0", "1 = 1",
"2 = 2", "X = X", mais jamais par exemple "0 = 1"
ou "3 = 7". En terme d'ontologie, c'est l'idée selon laquelle
toute chose X n'est qu'elle-même et jamais une autre.
Cela semble normal de penser ainsi, mais cette conception de l'Egalité et l'ontologie
qui lui est associée, l'ontologie de l'Identité donc (ontologie de type "X EST X"),
est non seulement extrêmement étroite, très faible et très insuffisante pour traiter l'Univers et tous ses aspects,
mais surtout très dangereuse, car elle conduit à nier des réalités de l'Univers.
Le problème de l'Identité, c'est tout simplement aussi le problème de la
Négation absolue,
le fait de dire que certaines choses n'existent pas dans l'Univers, ne sont pas vraies ou sont impossibles.
Or il existe une autre notion d'Egalité que nous connaissons très bien,
à savoir tout simplement l'Equivalence.
Nous l'utilisons très couramment, comme par exemple le fait de parler de l'"Egalité Homme-Femme",
de l'"Egalité entre deux pièces de 1 euro", de l'"Egalité entre deux feuilles de format A4 sorties d'une même rame de papiers",
de l'"Egalité entre deux articles de même modèles dans un rayon de magasin",
et plus généralement de l'Egalité entre deux choses A et B de même modèle.
Cette Egalité est infiniment plus générale,
et c'est elle qu'il faut pour raisonner avec l'Univers et l'étudier correctement.

A et B sont la même chose au sens de l'Identité.
Autrement dit, "A EST B"
au sens strict du verbe ETRE,
au sens de l'ontologie de l'Identité.
Dans ce paradigme et dans la logique qui y correspond,
des deux phrases contraires "A EST B" et "A N'EST PAS B",
seule la première est vraie, la seconde étant fausse.
L'Identité signifie que l'on n'a qu'un seul objet physique A,
et que B n'est qu'un autre nom pour désigner A.
On dit donc seulement A EST A ou A = A.
Pour indiquer qu'on parle de cette égalité très stricte, l'Identité,
on utilisera un double signe "=" et on écrira: A == A, B == B, A == B.

A et B sont la même chose au sens de l'Equivalence.
Autrement dit, "A EST B"
au sens large du verbe ETRE,
au sens de l'ontologie de l'Equivalence.
Dans ce paradigme et dans la logique qui y correspond,
les deux phrases contraires "A EST B" et "A N'EST PAS B" sont toutes les deux vraies!
En effet, "A N'EST PAS B" en tant que même objet physique (Identité),
mais "A EST B" en tant qu'objet physique équivalent à A (Equivalence).
C'est ici que réside toute la puissance de l'Equivalence,
qui peut se résumer par cette formule très forte:
"Distinct et pourtant Même" ou "Différent et pourtant Même",
ou encore: "Différents et pourtant Egaux"!
Cela a l'air d'une contradiction, puisqu'on dit une chose et son contraire!
Et pourtant il n'y a pas de contradiction,
car on traduit tout simplement un aspect très important de l'Univers:
Une chose A peut être une autre chose B
sans que les deux soient le même objet physique!
On a donc l'ontologie A EST B ou A = B,
dans toute la généralité et la puissance du verbe
ETRE.
La notion d'équivalence est très étroitement associée à celle de
modèle
ou encore de nom commun. Deux choses A et B
obéissant à un certain modèle
se caractérisent par un nom commun M, qui est celui
du modèle:
"Humain", "Chat", "Planète", "Livre",
"Nombre", "Information", "Ordinal", etc.
A chaque nom commun est associé un nom commun M donné,
qualifié d'ensemble quantique
ou d'ensemble ontologique,
ce qui veut dire que cet ensemble est l'ensemble de tous les M (de l'Univers TOTAL), et que
pour tout élément A de cet ensemble, on peut dire: "A EST UN M".
Très concrètement donc, c'est tout simplement ce modèle M ou ce
nom commun M ou cet
ensemble ontologique ou
quantique,
qui constitue l'équivalence entre A et B.
Autrement dit, si "A EST UN M" et "B EST UN M"
alors on dit que A et B sont équivalents ou égaux du point de vue de M,
ou modulo M, et on écrit donc:
A = B (modulo M).
Et l'ensemble ontologique défini par M, à savoir l'ensemble de tous les M,
est appelée une classe d'équivalence au sens du nouveau paradigme
(celui de l'Univers TOTAL, celui justement de l'Equivalence),
et non plus au sens étroit actuel de la notion (celui du paradigme de l'Identité).
Les classes d'équivalence sont tout simplement les ensembles.
Par exemple, si A et B sont deux humains,
on dira que A et B sont équivalents ou égaux du point de vue de
leur appartenance commune à l'ensemble de tous les humains,
ou qu'ils sont égaux modulo Humain.
On écrira donc: A = B (modulo Humain).
La classe d'équivalence est donc ici l'ensemble de tous les humains (de l'Univers TOTAL, il faut préciser).
De même aussi, deux feuilles A et B de Format A4
sont égales modulo Format A4.
On écrira donc: A = B (modulo Format A4).
La classe d'équivalence est donc ici l'ensemble de toutes les feuilles de Format A4 (de l'Univers TOTAL).
L'équivalence est donc une simple autre façon d'exprimer une coappartenance à un ensemble donné,
défini par un nom commun M. Et si aucune ambiguïté n'est à craindre sur
le modèle, le nom commun ou sur l'ensemble ontologique concerné par cette équivalence,
on écrira simplement A = B.
Loi de l'Equivalence Universelle ou Loi de l'Universalité
Le plus grand ensemble ontologique ou quantique est défini par
le nom commun CHOSE,
et cet ensemble est tout simplement l'Univers TOTAL,
l'Ensemble de toutes les choses.
Deux choses A et B sont donc égales modulo Chose.
L'Univers TOTAL est la plus grande classe d'équivalence qui soit.
Quand on ne précisera donc aucune classe d'équivalence particulière,
l'égalité A = B signifiera que la classe d'équivalence par défaut est tout simplement l'Univers TOTAL.
On a donc cette loi très simple et de très grande importance, la Loi de l'Equivalence Universelle ou Loi de l'Universalité:
Toutes les choses sont équivalentes du point de vue de leur appartenance commune à l'Univers TOTAL U,
de leur nature commune de modèle Chose.
Autrement dit, pour deux choses A et B, on a:
A = B modulo Chose, ou: A = B modulo U ou simplement: A = B.
Oui, oui, oui, deux choses distinctes, différentes, peuvent pourtant être la même chose!
Deux choses peuvent être la même chose sans être obligées d'être le même objet physique!
C'est le "Différent et pourtant Même"!
Etrange ou apparemment contradictoire, et pourtant il s'agit d'une vérité extrêmement simple et banale de l'Univers.
On ne réalise pas l'importance de ceci avec les objets ordinaires, mais à l'échelle de l'Univers TOTAL,
cette notion d'Equivalence est capitale, phénoménale,
extraordinaire, tout simplement miraculeuse!
Elle est très étroitement liée à la notion de générescence et de structure fractale
là où s'exprime toute sa puissance, là elle nous livre tous les secrets de l'Univers!
En disant: "Différent et pourtant Même", nous avons tout simplement dit
cette très simple et étonnante chose: "0 = 1"!
Autrement dit, à l'échelle de l'Univers TOTAL,
de la plus grande classe d'équivalence, cette égalité "0 = 1"
(une équivalence donc et non pas une identité) est une vérité, un théorème,
aussi vraie que le Cercle, aussi vraie que le Cycle!
Une égalité fausse au sens de l'Identité, mais vraie au sens de l'Equivalence.
Si donc on ne raisonne qu'en terme d'Identité, à savoir donc "0 = 0",
tous les secrets de l'Univers de type "0 = 1" nous échappent!
Or ce sont ceux-là les plus généraux, les plus fondamentaux, les plus puissants!
L'Identité nous conduit à NIER beaucoup, beaucoup de choses, alors que ce sont des vérités
et des réalités de l'Univers.
La notion d'Equivalence implique donc automatiquement la notion d'Univers TOTAL
(Ensemble de toutes les choses), et reciproquement dès qu'on parle d'Univers TOTAL,
cela signifie qu'on ne travaille plus avec l'ontologie de l'Identité,
mais qu'on passe à l'ontologie de l'Equivalence.
Cela revient à dire que dès qu'on parle de l'Univers TOTAL,
on abandonné la Négation absolue
au profit d'une Négation relative,
que nous appelons Alternation.
La raison est très simple: puisque les phrases contraires "A EST B" et "A N'EST PAS B"
deviennent toutes les deux vraies avec l'Equivalence, cela veut dire que la négation
contenue dans la phrase "A N'EST PAS B" n'est plus absolue, elle est relativisée, modérée.
Les couples Equivalence-Identité et Alternation-Négation: des dualités sur le modèle Ensemble-Elément
Le problème des paradigmes dans lesquels les dualités dysfonctionnent
Le couple Equivalence-Identité est un des nombreux exemples de notions duales,
ou de synonymes opposés, un curieux concept que l'on ignore sans doute actuellement.
C'est le fait pour deux notions d'être deux manières opposées ou contraires de dire exactement la même chose!
Il n'y a que dans le paradigme de l'Equivalence, le paradigme du "Différent et pourtant Même"
qu'on peut saisir ce genre de concept. Et justement, charité bien ordonnée commence par soi-même,
le couple Equivalence-Identité est exemple de notions duales,
comme aussi le couple Alternation-Négation.
Et toutes les notions duales ont un seul et même modèle fondamentale,
la dualité Ensemble-Elément!
D'autres dualités du même genre sont Variable-Constante, Infini-Fini,
Univers-Chose, Espace-Point, Temps-Instant, Evolution-Création, etc.,
ainsi que les dualités de type Oméga-Alpha, comme Plein-Vide,
Infini-Zéro, Univers-Particule, etc., jusqu'à la très importante dualité Absolu-Relatif,
quaisment synonyme de la Ensemble-Elément, car l'Ensemble est l'Absolu et l'Element est le Relatif.
Une notion peut s'opposer à une certaine autre dans une dualité, et s'opposer à une autre encore dans une autre dualité.
Mais cette opposition n'est jamais un combat à mort, mais une harmonie remarquable entre les deux notions,
sur le modèle Ensemble-Elément ou Absolu-Relatif.
Les problèmes commencent quand un membre d'une dualité pète les plombs et dysfonctionne gravement.
C'est en général la notion correspondant à Elément ou Relatif qui disjoncte
comme dans le duo Equivalence-Identité où c'est l'Identité qui est devenue fada
dans les paradigmes actuels. Plus gravement encore, il y a le duo Alternation-Négation,
où là où c'est carrément la Négation qui est devenue une Diablesse
(ou un Diable)!
L'une des rares exceptions à la règle est dans le duo Evolution-Création,
où là c'est carrément l'Evolution
qui est devenue folle depuis un certain Darwin.
Elle a oublié que sans la Création elle ne veut rien dire, de même que la notion d'Ensemble sans celle d'Elélement perd son sens.
Les deux membres de chaque dualité ne sont pas du tout identiques,
c'est-à-dire deux manières opposées de dire la même chose.
On verra au sous-titre Les différents degrés d'Identité et d'Equivalence,
la manière dont le couple Equivalence-Identité s'opposent en toute harmonie!
Mais d'abord commençons par comprendre ici le rôle et l'utilité de chaque membre du couple.
L'Identité est indispensable pour définir l'équivalence, une notion plus générale;
et sans les identités, l'équivalence perd son sens.
Cependant, c'est avec la notion d'Equivalence qu'il faut travailler, parce que justement plus générale que l'Identité.
Et parler d'Equivalence, c'est aussi parler automatiquement d'Identité.
En revanche, le danger est de ne voir que les identités sans leurs équivalences!
C'est le problème des Psychés d'Identité ou
Psychés de Négation.
C'est exactement comme le duo Ensemble-Elément.
Les éléments servent à constituer les ensembles, et sans les éléments donc, la notion d'ensemble est vide de sens.
Cependant, la notion d'ensemble est la notion supérieure, justement pour cette raison-là.
Et parler des ensembles, c'est évidemment parler aussi des éléments!
Et là aussi le danger est de ne voir que les éléments, les individualités,
sans voir l'ensemble et surtout l'importance des facteurs communs qui unissent ces individualités,
bref ce qui fait leur équivalence, leur égalité, malgré leurs différences et leurs particularités.
Le même raisonnement vaut pour le duo Alternation-Négation,
qui est une autre version exactement du même problème.
Ici, c'est la notion
de Non-Chose
trop séparée de Chose
qui pose problème, la séparation absolue entre Non-X trop séparée de X,
comme par exemple entre Non-Vivant et Vivant en biologie.
Cet aspect de la Négation est le Paradoxe de type
Paradoxe Sorite.
La Négation est nécessaire pour définir l'Alternation, dont elle constitue un cas important et fondamantal,
l'Alternation binaire,
celle qui sert à raisonner en terme binaire, en terme de Vrai et Faux, de Oui ou Non, etc.
Mais après c'est avec ce cas général de négation qu'on doit travailler,
et non pas se restreindre au cas binaire, qui non seulement sépare de manière absolue les choses
(là où la séparation ne doit qu'être relative), mais surtout à NIER de manière absolue.
C'est le problème des Psychés de Négation,
qui sont aussi des psychés d'Identité, ou des psychés individualistes, qui voient les éléments et les individus
séparément, mais qui perd de vue leur alternation (c'est-à-dire que l'Un est toujours l'Autre d'un certain point de vue), leur équivalence, leur ensemble.
Les Paradoxes de l'Identité ou les Paradoxes ignorés de la conception actuelle de l'Egalité
Dans la continuité de ce qui précède, les sciences actuelles sont dans des paradoxes de toutes sortes, ignorés jusqu'ici, car
car il faut un paradigme scientifique plus fort pour les mettre en évidence.
C'est donc dans le paradigme de l'Univers TOTAL et de l'Equivalence
que l'on peut enfin se rendre compte de tous ces paradoxes.
Au nombre d'eux, mettons en évidence les paradoxes ignorés de la conception actuelle de l'Egalité.
Paradoxe Ontologique de l'Identité
Le plus fondamental des paradoxes de l'Egalité actuelle est de savoir ce que signifie exactement le signe
"=" tel qu'on l'emploie dans les sciences actuellement.
En effet, derrière ce signe se cachent tout un tas de notions diverses, ambigües, mal définies,
très approximatives, qui permettent de dire tout et le contraire de tout sans annoncer clairement les couleurs,
d'utiliser en cachette ce que l'on nie officiellement, d'utiliser secrètement l'équivalence
"0 = 1" (parce qu'on ne peut pas s'en passer),
tout en la niant pourtant officiellement, en la déclarant paradoxale ou contradictoire!
bref de souffler le chaux et le froid comme le Diable!
La question simple qui se pose est la suivante: que faut-il entendre exactement par "A = B"?
Attention! malgré les apparences, cette question est très profonde et très subtile!
Alors voici quelques unes des réponses possibles, choississez la bonne (ou les bonnes) selons vous:
- 1) A EST B;
- 2) A EST B et B EST A;
- 3) A EST B mais B N'EST PAS A;
- 4) A et B sont strictement la même chose, à tous les points de vue;
- 5) A et B sont la même chose, mais seulement d'un certain point de vue M donné;
- 6) A et B sont deux noms différents pour désigner un seul et unique objet;
- 7) Partout où l'on voit A, on peut le remplacer par B et vice-versa;
- 8) Il n'existe absolument aucune chose, aucun point de vue, qui différencie A et B;
- 9) etc.
On peut prolonger la liste indéfiniment, mais ces réponses suffisent pour poser le problème,
qui est un problème d'ontologie,
c'est-à-dire de conception du très important et fondamental verbe
ETRE.
Les réponses 1 et 2 sont celles de l'ontologie générale, sans distinguer les deux types d'ontologie, car il y en a au moins deux,
les deux principales étant l'Identité et l'Equivalence.
La reponse 3 est l'ontologie de la représentation, de la désignation par un nom ou un symbole, du devenir, etc.
et plus généralement toutes les formes de la sémi-égalité, l'égalité à sens unique, qu'on peut noter par exemple:
A => B,
à lire par exemple: "A représente B", ou "A est un nom désignant B",
ou "Là où on voit A, il faut entendre B",
ou, dans le cas de l'ontologie de devenir : ou "A devient B",
ou: "Là où on disait A, il faut maintenant dire B".
L'ontologie de devenir, de représentation, et plus généralement les semi-égalités
sont très utilisées en informatique, par exemple dans l'opération d'affectation du genre:
A = 1, ou A = -5,
qui signifie simplement que ce qui est à gauche du signe "=" représente ce qui est à droite.
Et on a aussi l'opération d'incrémentation dans certains langages informatiques comme le BASIC, où l'on écrit par exemple:
A = A + 1, ou A = A + 20,
qui signifie que ce qui est à gauche du signe "=" devient ce qui est à droite.
Dans ces cas d'ontologie à sens unique, A EST B mais B N'EST PAS A.
Les réponses 4, 6, 7 et 8 sont tout simplement l'ontologie de l'Identité.
C'est la conception actuelle de l'Egalité, ce qu'un seul exemple suffit à démontrer:
actuellement, une égalité comme "0 = 1" est considérée comme fausse,
comme paradoxale, contradictoire, violant le sacro-saint principe de non-contradiction,
comme par exemple le montre cet article de Wikipedia,
"Contradiction",
au sous-titre "Preuve de l'absurdité de la contradiction".
Cette seule phrase résume comment on considère une égalité comme "0 = 1", mais
aussi la conception actuelle de l'Egalité.
"Un système d'axiomes qui permet de démontrer un théorème qui est une contradiction permet
de démontrer n'importe quoi (par exemple que 1=0, ou 1=1, ou 1=2, etc.)"
C'est là où les sérieux problèmes commencent,
qui sont plus que de simples problèmes de clarification des types d'ontologie (comme on vient de le voir),
mais un réel problème de mauvaise conception de l'Egalité, de l'Etre!
Pour mieux montrer cette mauvaise conception, terminons avec la réponse 5 le passage en revue des réponses
à la question posée concernant le sens à donner à l'égalité "A = B".
Cette réponse 5 définit l'Equivalence, le "Différent et pourtant Même",
un concept qui se résume simplement par: "0 = 1"!
L'Equivalence dit simplement que deux choses A et B
sont la même chose, dès qu'elles le sont d'un certain point de vue M,
c'est-à-dire simplement si elles possèdent un certain même
modèle M,
si elles répondent à un certain même nom commun M (Humain, Etoile, Ensemble, Nombre, Proton, Particule, etc.).
Alors même si A et B sont distincts et différents par ailleurs,
ils sont la même chose si l'on ne considère que le
modèle M.
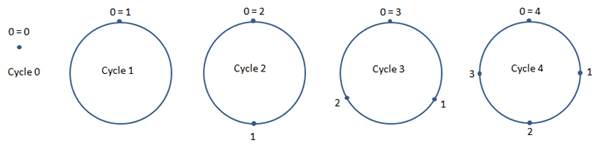
Par conséquent, le simple fait de dire que 0 et 1
sont deux nombres, donc qu'ils répondent au même modèle Nombre,
ou même plus généralement que 0 et 1 sont deux
choses, donc qu'ils répondent au même modèle Chose,
suffit à établir une équivalence entre ces deux nombres, le fait qu'une égalité existe entre eux.
Une égalité qui n'est pas si absurde que cela, d'autant plus qu'elle traduit une réalité géométrique
très banale, la logique des cercles et des cycles!
Le refus de dire "0 = 1" est tout simplement le refus d'écrire une égalité entre deux choses différentes,
c'est-à-dire justement NON-égales. C'est ici que la Négation intervient, c'est elle qui interdit cette égalité,
donc qui oblige à fonctionner dans l'ontologie de l'Identité, où l'on ne doit dire que "0 = 0",
"1 = 1" mais jamais "0 = 1".
Que l'on refuse l'ontologie de l'Equivalence, soit. Mais alors il faut être cohérent et ne pas utiliser clandestinement cette ontologie,
c'est-à-dire utliser l'Egalité ou le signe dans un sens qui est celui de l'Equivalence.
Or les sciences actuelles ne font que cela! La raison est toute simple: sans l'équivalence,
avec la seule identité, la science ne va pas loin! On ne peut faire le mondre calcul, résoudre la moindre équation,
si l'égalité sous-jacente n'est pas l'équivalente mais l'identité!
Pour s'en convaicre, considérons l'égalité suivante:
4 + 6 = 2 x 5.
Quel sens donner donc à cette égalité?
- Que "4 + 6" et "2 x 5"
sont strictement la même chose, à TOUS les points de vue?
- Que rien et absolument rien ne différencie "4 + 6" et "2 x 5"?
- Que partout où l'on voit "4 + 6" on peut le remplacer par "2 x 5" ou vice-versa?
- Bref, que "4 + 6" et "2 x 5" sont IDENTIQUES?
Dans ce cas alors considérons la phrase suivante: "'4 + 6' est une opération d'addition".
Alors puisque l'on a l'égalité "4 + 6 = 2 x 5", on peut donc remplacer dans cette phrase
"4 + 6" par "2 x 5", ce qui donne:
"'2 x 5' est une opération d'addition"...
Tout cela pour dire simplement que du point de vue de l'Identité,
"4 + 6" et "2 x 5" ne sont pas égales,
on n'a pas le droit de mettre un signe "=" entre les deux si l'on fonctionnait vraiment
dans l'ontologie de l'Identité, comme on l'affirme officiellement, et si l'on rejettait vraiment
toute égalité de type "Différent et pourtant Même", c'est-à-dire donc de type
"0 = 1", comme on l'affirme officiellement!
En effet, "4 + 6" est une addition de 4 et 6,
et "2 x 5" est une multiplication de 2 et 5.
Ce n'est pas du tout la même opération, ce n'est pas la même chose, mais deux choses très différentes!
Du point de vue de l'Egalité stricte, de l'Identié donc, on a seulement le droit de dire:
4 + 6 = 4 + 6 et 2 x 5 = 2 x 5, c'est tout!
L'identité sert ici entre autre à distinguer l'addition de la multiplication,
et aussi ne pas confondre les nombre 4 et 6 d'une part et 2 et 5 de l'autre. C'est son rôle fondamental
et ce rôle est très important, pour qu'on sache qui est qui, etc.
Et après alors entre en scène l'équivalence pour jouer son rôle, pour dire que malgré cette différence, cette distinction nette entre ces deux choses,
elles présentent un aspect commun, qui est leur résultat.
Si par exemple on introduit un nouveau nom commun, par exemple décasultat
pour désigner toutes les opérations qui donnent comme résultat 10, comme aussi par exemple
"20 / 2" ou "La racine carrée de 100", ce sont donc toutes des décasultats.
C'est ce modèle commun qui fait leur équivalence, et c'est bien cette équivalence que l'on exprime par:
4 + 6 = 2 x 5.
Que l'on refuse donc le paradigme de l'Equivalence, le "Différent et pourtant Même",
le paradigme du "0 = 1", et on ne peut même pas dire "2 + 2 = 4",
car d'un côté on une opération addition et de l'autre le nombre 4. Ce sont donc deux choses très différentes, car
4 ne veut pas forcément dire "2 + 2 ", car c'est aussi "2 x 2 ",
"8 / 2 ", etc.
Par conséquent, les sciences actuelles étaient dans un paradoxe très caché et très sournois de refuser
officiellement le "Différent et pourtant Même", le "0 = 1"
donc, et pourtant de l'utiliser en cachette, car sans cela la science ne va pas loin!
Si ce n'était que cela, ce ne serait pas trop grave, nous ne ferions pas tout un procès
juste pour une histoire d'égalité qui manque de rigueur.
Mais derrière ce paradoxe et d'autres se cache quelque chose de très mauvais, et c'est cela qui est grave:
ce paradoxe permet d'utiliser tous les avantages de l'Equivalence qui arrangent les affaires du Diable,
mais de NIER le meilleur de l'Equivalence, qui n'arrange pas du tout ses affaires, à savoir l'Univers TOTAL,
qui est le boulevard conduisant tout droit vers DIEU
(voir Nombres Cycliques, Algèbre Fractale, Algèbre Universelle,
et Générescence et Structure FRACTALE)!
Paradoxe la Variable, un crime contre l'Equivalence!
Voyons maintenant un autre exemple montrant les paradoxes cachés dans paradigmes actuels,
l'une des manières clandestines d'utiliser l'incontournable ontologie de l'Equivalence,
tout en la NIANT officiellement, et à travers elle ce dont elle est synonyme, à savoir l'Univers TOTAL et tout ce que cela implique.
Voyons le paradoxe de cette chose nommé les variables, l'usage que l'on fait par exemple actuellement de la célèbre variable
X.
Mais avant cela il faut juste présenter rapidement les proprités fondamentales de l'Equivalence,
qui seront étudiées plus techniquement dans la seconde partie de ce document.
L'équivalence ou l'égalité présente les trois propriétés fondamentales qui sont actuellement les suivantes:
1- Réflexivité: Toute chose A est équivalente (ou égale) à elle-même.
2- Symétrie: Si une chose A est équivalente (ou égale) à une autre chose B, alors B est aussi équivalente (ou égale) à A.
2- Transitivité: Si une chose A est équivalente (ou égale) à une autre chose B,
et alors B est équivalente (ou égale) à une autre chose C, alors A est équivalente (ou égale) à C.
La troisième propriété peut se dire ainsi: Si deux choses A et B sont équivalentes (ou égales) à une troisième chose C,
alors A et B sont équivalentes (ou égales).

A chaque fois nous avons ajouté "ou égale", car ces trois propriétés sont la définition actuelle
de ce qu'on appelle une relation d'équivalence (notée en souvent "≡"),
et qui est présentée comme un généralisation de l'égalité, ce qui est très bien.
C'est le vocabulaire que nous adoptions aussi auparavant avant de juger bon de le changer.
sinon, en passant au paradigme de l'Equivalence, nous aurions été obligé d'utiliser désormais le signe "≡"
comme nouveau signe de l'Egalité, l'actuel signe "=" signifiant alors "Identité",
car c'est le sens qu'il a actuellement.
Et plus précisément encore, l'actuelle égalité est en fait ce que qu'on appelle la Réflexivité de la
relation d'équivalence.
Autrement dit encore, au lieu de "Réflexivité", on aurait dû dire "Identité",
et au lieu de relation d'équivalence, on aurait dû dire simplement
relation d'égalité.
La manière de concevoir les choses montre qu'on s'est terriblement bridé, on s'est enfermé dans une boîte d'allumettes qui est l'Identité
et qu'on a prise pour l'Egalité, et on voyait l'Equivalence comme une généralisation de l'Egalité vérifiée seulement par certains objets mathématique et scientifiques,
et non pas comme une relation générale de la science et encore moins comme une relation fondamentale de l'Univers TOTAL!
Cela permettait de continuer à NIER l'Univers TOTAL, à déclarer impossibles ou paradoxales des situations en science qui sont la manifestation
de l'Univers TOTAL
(voir par exemple Les paradoxes de la théorie des ensembles)
tout en utilisant partiellement et même clandestinement des aspects puissants de l'Equivalence.
Et cela devient carrément indécent quand on utilise des concepts qui sont ceux de ce paradigme, comme par exemple la très puissante notion de Variable,
mais en violant de manière très sournoise les lois de la même Equivalence!
Très étranges artifices, contours et détours, très épouvantables complications inutiles des mathématiques et des sciences du Diable,
tout cela pour ne pas dire "0 = 1" et donc pour ne pas foncer tout droit vers Dieu!
Voyons maintenant enfin le Paradoxe de la Variable, un chef-d'oeuvre d'arnaque scientifique, d'autant plus grave que si la coupable se nomme les
mathématiques, la science réputée pour sa rigueur et pour son exactitude.
Ce paradoxe consiste à utiliser un objet, la lettre X par exemple, pour dire:
X = 0, X = 1, X = 2, X = 3, etc.
Donc on écrit à chaque fois une égalité entre différentes choses, 0, 1, 2, 3, 4, 5, ...
et une seule et même chose X. La transitivité de l'Equivalence ou de l'Egalité
oblige dans ce cas à écrire une égalité entre ces choses qui sont toutes égales à la même,
donc à dire tout simplement:
0 = 1 = 2 = 3 = 4 = 5 = ....
On déclare donc officiellement que des égalités comme "0 = 1", "1 = 2", etc.
sont absurdes, alors qu'on les utilise dans la notion de Variable!
Cette notion, telle qu'elle est utlisée actuellement, NIE donc l'Equivalence en niant la Transitivité,
alors que c'est l'Equivalence qui fait toute sa puissance!
On pourrait analyser bien d'autres paradoxes cachés dans les mathématiques et les sciences actuelles,
des incohérences qui ne se traduisent pas directement dans les pratiques des sciences,
qui ne ruinent pas les intérêts immédiats du Diable, mais qui ruinent gravement la Science en majuscule.
Car tous ces artifices l'empêchent d'être ce qu'elle devait être,
à savoir la Science de l'Univers TOTAL, la Science de l'Equivalence, la Science Limpide et Cristalline,
la Science de Dieu.
Les différents degrés d'Identité et d'Equivalence
Paradigme de l'Equivalence: le paradigme de la Structure fractale et du Cycle. Logique alternative
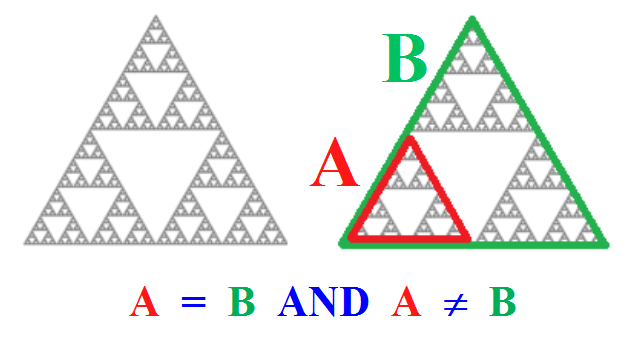
La structure fractale
est la situation par excellence où la notion d'Equivalence a toute son importance.
Ici, A et B ne sont pas la même chose au sens de l'Identité
mais sont la même chose au sens de l'Equivalence.
Ils sont en effet le même Triangle de Sierpinski.
Dans ce paradigme, les deux phrases contraires "A EST B" et "A N'EST PAS B" sont vraies sans qu'il y ait la moindre contradiction!
Nous appelons logique alternative la logique qui repose sur l'ontologie de l'Equivalence,
ce qui signifie que sa négation est la Négation relative.
Le cadre de cette logique est l'Univers TOTAL, l'Ensemble de toutes les choses. Elle possède les deux caractéristiques suivantes:
- Un énoncé donné P est toujours vrai (caractéristique que nous appelons le Principe d'Alternation)!
- Un énoncé P et sa négation non-P sont toujours vrais dans l'Univers TOTAL.
P n'est faux que dans un contexte donné de l'Univers TOTAL, que d'un point de vue donné.
Mais alors il est toujours vrai dans un autre contexte de l'Univers TOTAL, d'un certain autre point de vue.
Le Principe de non-contradiction
signifie alors simplement que P et non-P ne sont pas vrais
dans le même contexte ou selon le même point de vue, le mot "même" étant alors à comprendre au sens de l'Identité.
Voici un exemple simple de vérité qu'on énonce quand on raisonne en logique alternative:
"L'égalité "0 = 1" est fausse du point de vue de l'Identité, mais est vraie du point de vue de l'Equivalence"
Ainsi donc, la véracité de "0 = 1" n'est pas niée dans l'absolu comme en logique négative,
mais elle n'est niée que relativement à l'Identité (justement...), et affirmée relativement à l'Equivalence.
L'énoncé "0 ≠ 1" est évidemment une vérité en logique alternative,
mais "0 = 1" est une vérité supérieure, qui inclut la précédente.
Dans le paradigme de l'Equivalence, "0 ≠ 1" signifie simplement que
0 et 1 sont deux choses distinctes
(l'égalité qui est niée est précisément l'identité),
ce qui n'empêche pas du tout qu'elles puissent être égales autrement, c'est-à-dire équivalentes.
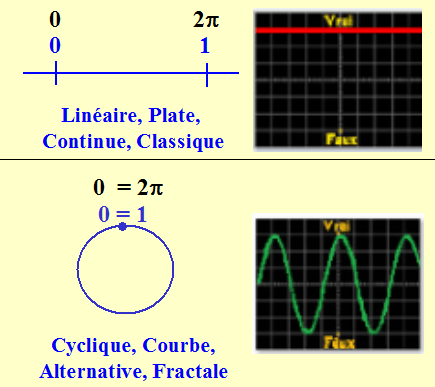


Le paradigme de l'Univers TOTAL est le paradigme de l'Equivalence et de l'Alternation, qui est aussi le paradigme du Cycle.
On ne raisonne plus avec la Logique classique (la logique qui se fonde sur le "Principe de NON-contradiction" d'Aristote).
On raisonne désormais en Logique Fractale, ou Logique Alternative, ou Logique cyclique.