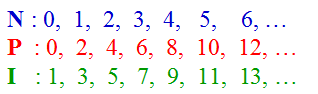Examen
des principaux types de "contradiction"
Paradoxe
du type 1
"Vrai ET Faux" ou "A ET non-A"

C'est
le cas général ou le cas standard de
ce qu'on appelle habituellement
une "contradiction", le cas direct. Toutes les contradictions quelles
qu'elles soient se ramènent à sa cas "Vrai ET Faux",
c'est-à-dire "Vrai ET non-Vrai". Et plus généralement,
toutes reviennent à dire : "A ET non-A",
où A est
une phrase, ou un certain attribut qui est affirmé et nié à la
fois, une certaine chose qui possède un
certain attribut B et ne le possède pas à la
fois (ce qui veut dire qu'il possède le contraire de
l'attribut B). Un tel objet A est
alors dit "contradictoire", mais je préfère
dans ce cas parler de "paradoxal" (j'y reviendrai
après les exemples). Toutes les contradictions (quelles
qu'elles soient) reviennent à parler d'un certain objet paradoxal,
qui possède à la fois un attribut et le contraire de
cet attribut. Alors la question logique de la véracité d'une
phrase contradictoire se transforme en la question "physique" de
l'existence d'un certain objet paradoxal, de sa possibilité,
de sa réalité. Il serait difficile de donner
tous les cas de figure dans les exemples qui vont suivre dans cette catégorie
générale et basique de la contradiction "A ET non-A",
puisque tout autre type de contradiction s'y ramène.
Tous posent un seul et même problème, celui de la négation,
et tous ont donc la même solution, que j'appelle l'alternation.
Voici quelques exemples de contradictions formulées dans cette forme générale "A
ET non-A" :
1a) "Il
pleut ET Il ne pleut pas";
1b) "La terre est plate ET La terre n'est pas plate" ou
: "La terre est ronde ET la terre n'est pas ronde" (problème
d'échelle; ça dépend de l'échelle à laquelle
on voit la terre, sur un terrain de foot ou de l'espace);
1c) "La somme des angles dans un triangle est de 180° ET La
somme des angles dans un triangle n'est pas de 180°" (problème
posé par le cinquième postulat d'Euclide en géométrie;
variante pus savante du problème d'échelle, l'exemple précédent);
1d) "Le nombre 1000 est petit ET Le nombre 1000 n'est pas
petit" (une version numérique du paradoxe
sorite ou paradoxe du tas : en partant de 0, à partir de
quelle valeur un nombre cesse d'être petit et commence à être grand ?);
1e) "Le nombre Gigantesque est infini ET le nombre Gigantesque
n'est pas infini" (par Gigantesque il faut entendre par exemple le
nombre écrit avec 1 suivi d'autant de zéros qu'il y a d'atomes
dans l'Univers; une subtile variante du paradoxe
sorite , mais avec les notions intuitives de fini et infini);
1f) "Dieu existe ET Dieu n'existe pas"(le problème
de la négation dans toute son excellence..., plus que
le problème de savoir ce qu'il faut entendre par "Dieu" ou
par le mot "exister");
1g) "Dieu peut faire l'objet d'une science exacte ET Dieu
ne peut pas faire l'objet d'une science exacte" (une variante du
problème précédent);
Ces
exemples sont volontairement choisis avec des mots plus ou
moins intuitifs, plus ou moins philosophiques, plus ou moins
provocateurs ou polémiques, comme par exemple avec le
mot "Dieu". Le but est justement de montrer l'importance
de ne pas se tromper de problème et de diagnostic en
discutaillant ou philosophant sans fin sur les mots et le sens à leur
donner; car le vrai problème est ailleurs,
et c'est simplement le problème
de la négation ! Peu importe le sens qu'on
donne aux mots de ces exemples, peu importe leur définition
(religieuse ou pas, philosophiques ou pas, intuitive ou pas,
rigoureuse ou pas, axiomatique ou pas, scientifique ou pas,
etc.), le simple problème qui se pose est qu'on a une
phrase du genre : "A ET non-A" !
On "s'en fout" pour l'instant de savoir ce que veut
dire A, quelle est sa définition, car
on est face au même modèle "A ET
non-A", et tout le problème est posé dans
ce modèle, et toute la solution y est également.
Si ce n'est le problème du mot de logique "ET" (appelé connecteur
de conjonction), alors c'est le problème
du mot de logique "non" (appelé connecteur
de négation). En fait, c'est lui qui
détermine toute la logique, ainsi que
le sens des mots qui servent à faire des phrases, des
choses sur lesquelles ces phrases portent, que ce soit la pluie,
le beau temps, la terre, le plat, le rond, l'angle, le triangle,
180, 1000, le petit, le grand, le fini, l'infini, le nombre,
la géométrie, l'espace, l'Univers, l'existence,
Dieu, la science, etc. Tout
dépend de la négation qu'on
utilise ! Qu'on la change et on change la logique et
le sens des mots et des choses,
et qu'on la change et on change la science !
Selon
la négation avec laquelle on fonctionne,
on ne voit pas du tout de la même manière la phrase "A
ET non-A", appelée une "contradiction",
ou ce qu'on appelle un objet "contradictoire".
Je
préfère à ce propos le terme de "paradoxal" (ou
de "paradoxe"), terme auquel je
donne le sens très précis suivant : "Chose
A possédant un attribut B et à la
fois le contraire (ou la négation)
de cet attribut B". Dans ce sens précis,
le mot paradoxe n'a pas un sens négatif ou péjoratif.
Et justement le sens négatif ou pas
négatif dépend de la négation
non qui figure dans "A ET non-A".
Si elle est primaire ou première ou absolue (je
reviendrai la-dessus après l'exament du troisième
type de paradoxe, mais aussi dans la partie Là où se
cache le Diable), alors c'est celle-même qui
est la contradiction, qui la provoque (contradiction
du pyromane-pompier ou du premier pyromane, du premier tueur
ou du premier cannibale, etc). Mais si elle est secondaire
ou seconde ou relative (là aussi je l'expliquerai),
alors elle est au contraire la solution à la
contradiction, la fin de la contradiction !
C'est une telle négation que j'appelle l'alternation,
et que j'invite à découvrir dans ce document.
Selon
cette nouvelle négation (l'alternation), "A
ET non-A" est simplement paradoxal (ou
un paradoxe), et ce mot est synonyme de singulier (ou
une singularité), de spécial ou spécifique (ou spécialité ou spécificité).
L'Univers (au sens le plus total du terme)
est la chose singulière ou spéciale par
exellence, à cause de son unicité obligée.
Il en resulte des propriétés très spécifiques,
qui se traduisent d'une manière ou d'une autre par un paradoxe "A
ET non-A". Mais un tel paradoxe est
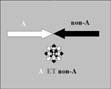
simplement comme la plaque (ou une feuille de papier) représentée
ci-dessous, Blanche au recto et Noire au
verso :

Quand
la plaque tourne suivant un axe comme le montre la figure,
elle présente alternativement la face Blanche (à interpréter
comme Vrai) et la face Noire (à interpréter
comme Faux). Et la plaque apparaît alors
comme Grise, une couleur inconnue et paradoxale
pour des êtres qui ne verraient la réalité qu'en
terme de Blanc OU Noir (c'est-à-dire SOIT
Blanc, SOIT Noir, mais pas "Noir
ET Blanc"). De même, la rotation de
la plaque rectangulaire produit un objet en trois
dimensions, le Cylindre de révolution,
combinant les propriétés d'un Rectangle (plein)
et d'un Cercle (ou disque), des objets en deux
dimensions. Pour des êtres vivant en deux
dimensions, cet objet "étrange" et "inconcevable",
qui est à la fois un rectangle et un cercle,
est "contradictoire" donc ne peut exister.
Mais il est tout simplement paradoxal dans
leur monde en deux dimensions, mais tout à fait normal et
il EXISTE dans un monde en trois dimensions !
C'est
le problème que nous avons avec notre logique bivalente,
qui ne voit la vérité qu'en terme de "Vrai
OU Faux" (mais pas "Vrai ET Faux").
Nous ne voyons pas comment il peut pleuvoir et à la
fois ne pas pleuvoir (exemple 1a). Et pourtant
il suffit de penser à l'objet Univers. Il
pleut quelque part dans l'Univers,
et quelque part il ne pleut pas. C'est comme
si nous voyons le même Univers, ici
sous sa face de pluie, et ailleurs sous sa
face de non-pluie. La phrase "Il
pleut ET Il ne pleut pas" est un exemple
d'universalité, c'est-à-dire
une propriété de l'objet Univers, étudié comme
n'importe qu'elle objet, comme le proton ou un pulsar par exemple.
L'exemple 1b pose simplement le problème de l'échelle à laquelle
on examine le même Univers, ici son
sous-objet qu'est la terre, plate vue
sur un terrain de foot, et ronde vue de l'espace.
L'exemple
1c appelle cette très importante remarque : on considère
que c'est une contradiction quand la chose A et
son contraire ou non-A sont
mises directement dans la même phrase,
comme par exemple dans "Il pleut ET Il
ne pleut pas", ou si les deux contraires A et non-A sont
dans un même système d'axiomes
d'une théorie T, appartenant à un
domaine général D donné (ici
la géométrie). Mais si A appartient à une
sous-théorie T1 ou branche du domaine D (ici
par exemple la géométrie euclidienne), et non-A à une
sous-théorie ou une branche T2 du même
domaine D (ici par exemple la géométrie
non-euclidienne), on n'appelle pas cela une contradiction...
Or la phrase "A ET non-A" (ici l'exemple
1c) exprime bel bien une vérité générale,
du domaine général D (ici une
vérité de la géométrie). Comme
quoi on voit la contradiction quand on
veut, mais on ne la voit pas quand
on ne veut pas, une sorte d'"hypocrisie" scientifiquement
et savamment bien organisée donc...
Suivant
ce modèle, si par exemple je dis une chose A en public et
exactement le contraire de A (ou non-A)
en privé, je ne me contredis pas,
puisque je n'ai pas dit cela dans le même domaine ou
dans le même contexte. Or la réunion du public et
du privé constitue un domaine (ou
un contexte) plus vaste, dont ceux-là sont
des sous-domaines (ou sous-contextes). Et le cas échéant,
l'objet Univers est la réunion de tous
les contextes, c'est le contexte le
plus grand qui soit. Donc
finalement j'ai bel et bien dit A et son contraire dans
un certain même domaine ou contexte ,
il est plus grand c'est tout... Le cas échéant,
c'est l'Univers, le contexte le plus grand.
J'ai dit une chose et son contraire dans
l'Univers. Il s'agit d'un type de paradoxe,
appelé par exemple hypocrisie...
Avec
les exemples 1d à 1g se pose un problème crucial
de la négation, le problème
du clivage, de frontière ou
de la séparation entre les mots,
les domaines, bref les choses.
Cela va de la simple question de définition des
mots, au problème très fondamental de l'ontologie,
le problème de savoir ce qu'est ou n'est
pas une chose. Où commence
par exemple la notion de petit, où s'arrête-t-elle,
et où commence celle de grand ? C'est
la même question avec les notions de fini et infini,
et plus généralement plus profondément
la séparation entre nombre et non-nombre !
Et plus profondément encore se pose la question de savoir
où commence ce qu'il faut appeler science et
où finit-elle exactement, et commence par exemple la philosophie ou
la religion, donc la non-science ?
Et plus profondément encore, où faut-il commencer à parler
de l'existence d'une chose et
où s'arrête cette existence,
donc où commence la non-existence ?
Et enfin, où commence la notion de Dieu et
s'arrête-t-elle, donc où commence le non-Dieu ?
C'est
tout le problème
même de la négation, et en conséquence
tout le problème de la contradiction,
celle qu'il faut appeler la vraie ! La contradiction n'est
pas de dire "A ET non-A", mais la
contradiction dépend de la négation avec laquelle
on dit "A ET non-A". Si elle est primaire ou absolue (on
comprendra ce que cela veut dire par la suite), alors non seulement
elle nie (sans le savoir forcément)
les réalités comme la couleur Grise ou
le Cylindre, et, le pire !, elle nie l'existence de
la plus grand des réalités : l'Univers !
Elle ne nie parce qu'elle le juge "contradictoire" (c'est-à-dire contraire à la logique, à la vérité et à la réalité),
alors qu'il n'est que paradoxal (c'est-à-dire
simplement hors des limites étroites de notre logique
avec son archaïque principe
de non-contradiction*) ! Mais avec l'alternation,
une négation qui est secondaire ou relative (on
comprendra aussi ce que cela veut dire), on peut enfin découvrir
toutes les propriétés spécifiques de
l'Univers, dont celle-ci : L'Univers est
la chose qui posséde tous les
attributs. Autrement dit, l'Univers est toute
chose, et donc c'est simplement la définition
par excellence qu'il faut donner au mot Dieu.
Il suffisait simplement de changer de négation,
on voit clair dans les mots et
les choses...
Paradoxe
du type 2
Paradoxe de Russell ou Paradoxe du menteur :
"Si c'est Vrai alors c'est Faux; et si c'est Faux alors
c'est Vrai" ou "A <=> non-A"

On
appelle aussi une contradiction le fait d'exprimer
une équivalence logique entre une chose
A et son contraire non-A. Intuitivement,
cela veut dire qu'une chose et son contraire signifient
la même chose. C'est le type du Paradoxe
du Menteur, dont une forme plus générale
est le Paradoxe
de Russell ou Paradoxe du barbier.
2a) "Si
je gagne la partie, alors je perds la partie; et si je perds
la partie, alors je gagne la partie" (paradoxe
de Bernardo, le joueur d'échecs solitaire);
2b) "Si le barbier se rase lui-même, alors il ne se rase pas
lui-même; et s'il ne se rase pas lui-même alors il se rase lui-même" (paradoxe
du barbier, celui qui rase tous les hommes du village qui ne se rasent pas
eux-mêmes; forme populaire du Paradoxe de Russell);
2c) "Si
l'ensemble A appartient à lui-même, alors il n'appartient
pas à lui-même; et s'il n'appartient pas à lui-même,
alors il appartient à lui-même" (paradoxe
de Russell dans sa forme standard, ou paradoxe de l'ensemble
A des ensembles non-éléments d'eux-mêmes
).
"Le
barbier A d'un village rase tous les hommes du village qui
ne se rasent pas eux-mêmes. Le barbier se rase-t-il
lui-même ?". C'est le
paradoxe découvert par le logicien Bertrand
Russell (1872-1970). Remarquons que le problème
exactement que le suivant : "Un Dieu A est le créateur
de toutes les choses qui ne se créent pas elles-mêmes.
Ce Dieu se créet-il lui-même ?" C'est
le même modèle (notion d'une
extrême importance dans la Science
Nouvelle) de problème, donc c'est la même
solution, la même réponse par Oui ou par Non.
La puissance de cette notion de modèle vient
de ce qu'elle se moque complètement du sens a priori
qu'on donne aux mots et des discussions philosophiques subectives.
Elle se démarque aussi complètement de la philosophie
axiomatique actuelle, en ce qu'elle ne fait pas non plus abstraction (au
sens le plus naturel du terme) du sens naturel des mots,
faisant une science où Dieu par exemple (ou son sens
naturel) est exclu du langage. Mais la nouvelle notion de modèle (celle
de l'alternation) se contente de jouer son rôle, à savoir
d'établir les vérités universelles,
qui s'appliquement à TOUTES les choses concernées
par une forme une autre du modèle.
Ici par exemple, les vérités que ce modèle
va établir vont s'appliquer aussi bien au barbier qu'à Dieu, à la
notion de se raser comme à celle
de se créer. Si
donc le barbier A ne peut
pas exister, alors ce Dieu A ainsi
défini ne peut pas exister non plus.
Mais si l'un existe, l'autre existe aussi,
et vice-versa. Et si l'un se rase lui-même,
alors l'autre se crée aussi lui-même,
etc. Pour savoir la bonne définition à donner à une chose donnée,
ce qu'elle peut être ou ne
pas être, dans tel contexte ou
dans tel autre, etc., il suffit simplement de laisser parler
les modèles qui l'impliquent. Ce
sont les modèles qui donnent leur
sens aux choses, et c'est là où le
rôle de la négation est cruciale.
Car selon la négation avec laquelle
on fonctionne, cela conduit à affirmer un
attribut ou affirmer une existence,
ou au contraire à nier cet attribut
et cette existence ! Bref la réponse à une
question dépend de la négation avec
laquelle on fonctionne; d'où la gravité et
la haute importance de la négation,
dans la recherche de la vérité,
dans la compréhension de la réalité !
Et
maintenant, voici comme le Paradoxe de Russell se présente
en théorie des ensembles : "Un ensemble A a
pour éléments exactement pour éléments
tous les ensembles qui n'appartiennent pas à eux-mêmes.
A appartient-il à lui-même ?" On doit
alors, en vertu du fameux "raisonnement par l'absurde" (qui
repose sur le principe
de non-contradiction), dire que l'hypothèse
de l'existence d'un tel ensemble A est fausse,
car on se trouve devant ceci, appelé une contradiction
: "Si
l'ensemble A appartient à lui-même, alors il n'appartient
pas à lui-même; et s'il n'appartient pas à lui-même,
alors il appartient à lui-même". Autrement
dit, l'ensemble A, qui est donc un objet "contradictoire" (car
il possède à la fois un attribut : l'auto-appartenance,
et le contraire de cet attribut : la non-auto-appartenance),
ne peut pas exister. Donc le barbier ou Dieu
ainsi défini ne peut pas exister, parce
qu'il est "contradictoire". Mais
c'est ce que j'appelle un objet paradoxal,
et il peut bel et bien exister ! Et il se
trouve simplement que cet ensemble A paradoxal
n'est autre que l'Univers, car c'est aussi
simplement le problème de l'Univers :
"Un
Univers appartient à toutes les choses qui n'appartiennent
pas à elles-mêmes. Cet Univers appartient-il à lui-même
?" C'est la version du problème concernant
l'Univers, en tant qu'élément
universel, la particule la plus élémentaire
(l'infiniment petit), qui appartient à toutes choses,
bref en tant qu'ensemble vide ! Et la version
en tant qu'ensemble universel, qui a toutes
les choses comme élément (l'ensenble
de toutes les choses), bref en tant qu'ensemble
plein : "Un Univers a comme éléments
toutes les choses qui n'ont pas elles-mêmes comme éléments.
Cet Univers a-t-il à lui-même comme élément
?" Un Univers ainsi défini
ne peut pas exister. Et maintenant Bernardo
le joueur solitaire au jeu d'échecs peut-il exister (exemple
2a) ?
"Un
joueur au jeu d'échecs A gagne la partie contre tout
joueur qui ne gagne pas contre lui-même. Ce joueur
gagne-t-il contre lui-même ?"
Bernardo
est le compagnon muet (mais pas sourd...) de Don Diega (alias
Zorro), qui joue souvent contre lui-même aux échecs.
Quand Don Alexandro le père de Don Diego lui demande qui
gagne, celui-ci répond en plaisantant : "on ne sait
pas, car la partie se termine souvent par une dispute...".
Au delà de l'anedote, il n'empêche qu'on peut tout à fait
jouer contre soi-même aux échecs, jouer avec une
couleur le meilleur coup que l'on pense, puis se placer de l'autre
côté de l'échiquier (ou le retourner ou se
projeter mentalement de l'autre côté) pour voir
la situation du côté de la couleur opposée
et jouer le meilleur coup, et ainsi de suite. Pour avoir joué dans
un club, c'est ainsi que je travaillais (comme beaucoup d'ailleurs)
les lignes de jeu. Le but peut justement consister à trouver
quelque chose plus fort que ce qu'on a trouvé avant ou
que ce que l'on connaissait, bref d'être plus fort que
soi-même, et pourquoi pas (si on est programmeur) de mettre
au point un logicien qui nous défie. Alors en jouant contre
le logiciel qu'on a créé (en jouant donc contre
une machine programmée avec notre propre intelligence...),
on joue contre soi-même.
Le
problème de toute façon ne concerne pas la qualité éventuelle
du jeu quand on joue contre soi-même, ou l'intérêt
du jeu puisqu'on est censé connaître le plan de
l'adversaire qui n'est que soi-même. Mais la simple question
est que c'est une possibilité (singulière certes)
mais une manière de jouer à ce jeu. Et c'est
vrai alors que quand on gagne on perd aussi et que quand on
perd on gagne aussi.
Ceci est
une situation concrète qui montre que le paradoxe de
Russell n'est pas si contradictoire qu'on le pense couramment.
C'est parce qu'on ignore l'existence de situations singulières ou
de choses spéciales dans l'Univers (la
première et la plus singulière de toutes étant
justement l'Univers lui-même !) où ce
genre de propos non seulement a un sens, mais est une vérité.
L'Univers est par définition l'ensemble de toutes
les choses, le TOUT. C'est le contexte global, le
plus large qui soit, dans lequel tout et absolument
tout se passe ! Donc il y a tout et
son contraire dans l'Univers,
autrement dit il possède les attributs et les contraires
des mêmes attributs ! L'Univers est
donc forcément "contradictoire",
sans pourtant l'être !
Autrement
dit encore, l'Univers est par nature unique,
puisqu'il est le TOUT. Comme Bernardo, l'Univers est
donc seul devant son échiquier, qui
n'est autre que lui-même encore ! L'Univers n'a
donc que lui-même pour "jouer" ses "parties",
donc il gagne contre lui-même et perd contre lui-même.
Il est toujours différent de lui-même (puisqu'il évolue),
et pourtant finalement il est toujours égal à lui-même,
puisqu'il se compare à rien d'autre qu'à lui-même.
Les paradoxes du type de celui de Russell décrivent
tout simplement les propriétés de la singularité suprême
qu'est l'Univers (voir
aussi la vidéo Toute
la lumière sur les Paradoxes) !
Paradoxe
du type 3
Paradoxe de la Double Négation
ou Paradoxe d'Eden ou Paradoxe de l'Interdiction
ou Paradoxe du Cannibale :
non (non A)
Une situation est actuellement dite contradictoire si elle
exprime une chose et
cache en même temps le contraire de
la même chose. Dans le type de "contradiction" abordé ici,
ce contraire n'est pas directement exprimé dans la situation, comme
dans les cas précédents. Mais ce contraire est en arrière-plan,
et il faut souvent faire une déduction plus ou moins subtile pour
le mettre en évidence.
Si
par exemple je dis : "Tout est permis",
on peut déduire qu'il est permis aussi
que "Tout ne soit pas permis", d'où le
contraire qui "contredit" la première phrase.
Une autre façon de mettre en évidence la "contradiction",
c'est de dire : Si "Tout est permis", alors "L"interdiction
est interdite" (slogan de Mai 68), donc une chose
au moins est interdite, ce qui contredit la phrase "Tout
est permis". Ce type spécial de "contradiction" est
celui qui caractérise les phrases et les conceptions
d'Hubertelie, celles de sa Science
de l'Existence...
3a) "Il
faut nier la négation" (paradoxe de la double
négation ou paradoxe du "non non", ou de
l'affirmation, ou du "Tout est affirmation");
3b) "C'est faux qu'une chose puisse être fausse" (paradoxe
du "faux faux" ou paradoxe de la vérité ou du "Tout
est vrai");
3c) "Cela ne doit pas exister qu'une chose puisse ne pas exister" (paradoxe
du Théorème
de l'Existence ou paradoxe du "Toute chose existe");
3d) "Il est impossible qu'une chose soit impossible" (paradoxe
de l'"impossible impossible", ou de la possibilité, ou du "Tout
est possible");
3e) "Oméga est le nombre entier naturel plus grand que tous
les nombres entiers natuels" ou simplement : "Oméga
est le plus grand de tous les nombres" (paradoxe de l'infini ou paradoxe
du dernier nombre ou paradoxe du dernier ordinal ou paradoxe
de Burali-Forti (w));
3f) "Il
est interdit d'interdire" ou "J'interdis l'interdiction" (paradoxe
du slogan de Mai 68 ou paradoxe de la permission ou du "Tout est
permis");
3g) "Il faut tuer tous les tueurs" ou "J'ai tué tous
les tueurs" (paradoxe de la peine de mort ou du dernier tueur);
3h) "Il faut manger tous les cannibales" ou "J'ai
mangé tous les cannibales" (paradoxe de Madokiya ou paradoxe
du dernier cannibale).
C'est
le type par excellence de pseudo-contradiction !
C'est le manque de profondeur dans la compréhension
du problème
de la négation (problème qui sera étudié en
profondeur) qui fait penser à une contradiction. De
plus, ces propos sont simplement une application spéciale
de la double négation: non
(non A) = A. Nier deux fois de
suite revient à ne pas nier; et là on ne
nie pas, il ne peut pas y avoir de contradiction.
En fait, c'est celui qui veut démontrer la contradiction qui
introduit le premier la négation, et
donc qui de ce fait provoque lui-même la contradiction qu'il
démontre ! Une très subtile affaire de pyromane-pompier.
C'est
pourquoi le Paradoxe
du Menteur (w) ne se produit pas avec la phrase "Je
dis la vérité" (car elle ne comporte
aucune négation) mais avec la phrase "Je
mens" (qui elle comporte une négation, celle
contenue dans le verbe mentir). De la même
le Paradoxe de Russell ne peut pas se produire avec les "ensembles
qui appartiennent à eux-mêmes" mais avec
ceux qui "n'appartiennent pas à eux-mêmes".
Il faut nécessairement la négation pour
que la contradiction soit possible. Autrement dit, avec la
version du barbier, l'idée du "barbier qui rase
tous les hommes qui se rasent eux-mêmes" ne
provoque aucune contradiction, mais cela se produit avec ceux
qui "ne se rasent pas eux-mêmes".
Pour
la même raison, celui qui veut démontrer que la
phrase "Tout est vrai" ou "Tout
est possible" (qui est absolument affirmative ou positive et
ne comporte donc aucune négation) est contradictoire,
est obligé d'introduire lui-même le premier la négation en
faisant un raisonnement du genre : "Si tout est vrai,
alors il est vrai aussi qu'il existe quelque chose de faux (ou
de non-vrai)", ou : "Si tout est
possible, alors il est possible aussi qu'il y ait au moins
une chose impossible (ou non-possible)".
C'est cette première négation qui
provoque elle-même la contradiction (voir la partie Là où se
cache le Diable), qui oblige une seconde négation
pour annuler la première, donc pour supprimer le paradoxe.
Ce
problème de la négation (qui est le problème)
et de la double négation (qui est la solution) est plus
flagrant avec les exemples concret 3g et 3h. Si on ne distingue
pas les deux négations (ici les deux mots "tuer"),
on dira simplement que tuer, quand bien-même c'est un
tueur, c'est être soi-même un tueur, point final;
d'où la contradiction que l'on croit relever dans le
problème. Autrement dit, il est contradictoire de dire
qu'on tue tous les tueurs, car le dernier tueur ne pourra pas être
tué, donc on ne peut pas les tuer tous. Mais la solution
est fort simple : là où il n'y a pas de premier
tueur, là non plus il n'y a pas de deuxième ou
de dernier tueur, et le problème de tuer
tous les tueurs ne se pose pas ! La contradiction est
introduite par le premier à tuer quelqu'un,
ou le premier à manger quelqu'un (dans
le cas du problème des cannibales, 3h) ! Et alors "Tuer
le tueur" devient nécessaire, tout comme "manger
le cannibale", et plus généralement "nier
la négation".
Plus
techniquement, c'est un simple problème de l'autoréférence,
qui est le problème général de la récurrence et
de son contraire la récursivité,
ici avec le cas particulier de la négation.
Il s'agit en fait d'un faux problème,
car pour qu'il y a ait récurrence il
faut deux conditions : d'abord ce qu'on appelle l'"hérédité",
c'est-à-dire la loi qui dit comment avoir l'étape
suivante à partir de l' étape précédente.
L'hérédité seule ne fait
pas la récurrence, car il faut pour
cela en plus l'étape initiale, le déclenchement
du processus. Sans
ce déclenchement le processus ne démarre pas,
il n'y a aucun engrenage (s'il s'agit d'un processus négatif),
donc il n'y a aucun problème, aucune contradiction.
Si cette le phénomène de réccurrence est
lancé, alors c'est son contraire, la récursivité (la
récurrence en l'envers) qui doit à un moment
ou à un autre être enclenché si on veut
inverser le processus et revenir à l'état d'avant
le déclenchement du fléau. L'étape finale
dans le processus inverse est le faux problème posé par
exemple par le "dernier tueur", le "dernier
cannibale", le "dernier à interdire",
le "dernier à nier", etc., et aussi par le "dernier
nombre". Dans le sens de la récurrence le dernier est
l'"infini", qui permet de dire que
le processus est totalement accompli, et dans le sens de la récursivité le dernier est
le "zéro".
Voici
sommairement des problèmes ainsi qu'un petit aperçu
de la solution. Je
propose dans ce document une analyse très profonde et
plutôt complète du problème de la contradiction,
très différente de la vision qu'on a actuellement
de la chose. Le
diagnostic du problème est actuellement mal posé,
car la clef du problème est simplement la négation.
On découvrira au fur et à mesure aussi le paradigme de
la Science
Nouvelle, à savoir très précisément
ce que j'appelle l'alternation.
La
simple solution
Chose,
existence, ensemble, Univers...
Le mot
clef le plus fondamental de la Science
Nouvelle est chose.
On a sans doute remarqué l'emploi fréquent
et uniforme que je fais de ce terme dans ce document
ou dans tout
autre,
tout comme aussi les notions d'existence et
d'ensemble, qui sont respectivement
le deuxième
et le troisième mot clef. (Voir
aussi Chose,
Existence, Ensemble).
Une chose est tout
ce dont on parle, sans aucune restriction.
Une chose est un homme,
une femme, un arbre,
un caillou, une contradiction,
un mensonge, le bien,
le mal, l'amour,
la haine, un proton,
un neutron, un électron,
un neutrino, le soleil,
la lune, une étoile,
la mathématique, la logique,
une existence, un ensemble,
la science, internet, Dieu, Diable,
un ange, Harry Potter,
une chose..., etc. On
peut dire que la chose nommée Dieu (peu
importe ce qu'on entend par ce mot) existe ou
non. Mais on ne peut refuser à Dieu d'être
une chose.
Les choses seront
souvent désignées par les lettres A, B, C, D,
etc. Bref, toutes les fois que dans cette science on
verra ce qu'on appelle couramment une variable (la
variable star étant X majuscule
ou x en minuscule), cela
signifie avant tout une "chose",
avant toute autre précision sur la chose en
question.
La Science
Nouvelle se déroule dans l'Univers,
défini très précisément
comme étant l'Ensemble de toutes les
choses, ou simplement le TOUT.
C'est donc l'Univers au sens le
plus total, sans aucune restriction.
Appelons-le U dans ce document.
La
vraie contradiction, c'est nier la réalité !
Le
principe de non-contradiction
"Il
est impossible qu’un même attribut appartienne
et n’appartienne pas en même temps et sous le même
rapport à une même chose" (Aristote, Métaphysique,
1005 b 19-20).
Sous
sa forme ontologique simple, le principe
de non-contradiction formulé
ainsi par Aristote signifie qu'une chose A ne
peut pas à la fois être et ne
pas être. En termes d'existence,
cette chose ne peut pas à la fois exister et ne
pas exister.
Une contradiction est
donc le fait d'affirmer en même
temps une chose A et son contraire.
Mais il
y a contradiction et contradiction !
Encore faut-il donc que ce qu'on appelle une "contradiction"
ne soit pas une problème venant de notre logique.
Il faut donc étudier la question très profondément,
afin de découvrir
où se trouve la vraie contradiction. La
vraie contradiction, c'est nier
une réalité !
L'Univers
est "paradoxal"... mais pas contradictoire !
Le pire qui
puisse arriver à la science (et c'est arrivé !)
est d'appeler une "contradiction"
une propriété de l'Univers que
notre logique est trop étriquée ou trop pauvre pour appréhender.
Et si pour cela on en vient à déclarer des choses qui reviennent
à dire qu'il est impossible que
l'Univers
existe (ou
même simplement à nier des réalités),
sans offrir aucune chance de véracité au contraire de nos
propos,
alors
nous
sommes
simplemnt
coupables
de la pire des contradictions; car
nous nions simplement la Réalité suprême
!
L'Univers est par définition l'ensemble
de toutes les choses, le TOUT au
grand complet donc. Et qui dit TOUT, dit simplement que dans
l'Univers il y a tout et
son contraire ! Autrement dit donc, l'Univers est
l'objet par excellence auquel tous les attributs appartiennent,
et aussi la négation (ou le contraire)
des mêmes attributs ! Au sens de la
conception actuelle de la contradiction, l'Univers est
l'objet le plus contradictoire qui soit.
Mais je
préfère qu'on parle plutôt d'objet paradoxal,
sans donner au mot "paradoxe" le
sens négatif qu'il a actuellement. La contradiction est
contre la logique de l'Univers, elle s'oppose à la
réalité, à la vérité,
tout simplement; tandis que le paradoxe heurte
la logique courante, et nous invite à changer
de logique, de paradigme, de philosophie, etc., pour pouvoir
comprendre ou expliquer l'Univers d'une
manière adéquate.
Pour montrer
un exemple de paradoxe qui n'est pourtant pas
une contradiction, considérons l'ensemble N des nombres
entiers naturels : 0, 1, 2, 3, 4, 5, 6, 7....
Il est fait du sous-ensemble P des nombres pairs : 0,
2, 4, 6,..., et du sous-ensemble I des nombres
impairs : 1, 3, 5, 7,.... Notre logique nous fait admettre
volontiers qu'il y a autant de nombres pairs que d'impairs, puisqu'on
peut les associer
ainsi deux à deux :
Tous
les nombres, sans exception, sont ainsi associés,
et on appelle cette opération une bijection, qui est
le critère pour dire que deux ensembles ont un même
nombre d'éléments. Et notre logique nous dit
que P ou I ont deux fois
moins d'éléments que l'ensemble N tout
entier, puisque ces deux sous-ensembles ont le même
nombre d'éléments et que la somme de leurs éléments
donne N. Ceci est parfaitement exact ! Et
pourtant aussi, ces deux sous-ensembles ont exactement le
même nombres d'éléments que l'ensemble N tout
entier ! En effet, on peut associer par une bijection les éléments
de N, P et I ainsi,
sans épuiser aucun avant l'autre :
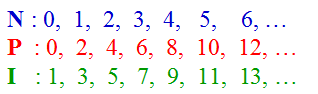
Les
deux premières lignes disents cette grande vérité selon
laquelle tout nombre (première ligne) à son
double et un seul (qui est donné par la seconde ligne);
et que tout nombre pair (seconde ligne) a sa moitié et
une seule (première ligne). Donc les deux premières
lignes ont effectivement le même nombre d'éléments.
Et quant à la troisième, il suffit d'ajouter à chaque
fois 1 à la seconde pour l'avoir; il y a donc une
correspondance parfaite les deux dernières lignes,
et entre les trois lignes. La partie a donc le même
nombre d'éléments que le tout. Le
nombres des éléments de N est infini,
et ceci est une propriété de l'infini.
Autrement dit, il n'y a pas plus d'éléments
dans N que dans P, par
exemple. Et pourtant il manque bien les impairs à P pour
avoir le même nombre d'éléments que N.
Cette
situation heurte l'intuition et la logique courante, elle
montre que
cette phrase, qu'on le veuille ou non, est vraie : "N
a plus d'éléments que P ET N n'a pas plus
d'éléments
que P". Ceci correspond à la réalité même,
elle est en conflit avec le principe de non-contradiction,
et on ne s'en sort que par les vertus de l'artifice (l'actuelle
méthode axiomatique), qui permet de travailler dans
un langage séparé du langage courant, et
dans lequel il est impossible d'énoncer cette réalité qui
crève les yeux et la logique : "N a
plus d'éléments que P ET N n'a pas plus d'éléments
que P".
Ceci
est un simple exemple de paradoxe,
qui est une des nombreuses manières d'exprimer le paradoxe
de l''infini. En voici d'autres : "L'infini
est plus petit que lui-même ET l'infini est plus grand
que
lui-même" (ou 'L'infini est
plus petit que lui-même ET l'infini n'est plus petit
que lui-même"). Une autre version
dans le langage des ensembles est : "Le dernier
oridinal appartient à lui-même ET le dernier ordinal n'appartient
pas à lui-même" (pour plus de détails, voir la vidéo Toute
la lumière sur les Paradoxes).
Ce
sont autant de manières d'exprimer des propriétés importantes
de l'Univers, et autant de paradoxes
de l'Univers. On appelle cela des"contradictions",
au lieu simplement de comprendre que le principe
de non-contradiction a
ses limites et qu'il ne permet pas d'accéder à toute
la réalité, à toute la vérité.
Voyons
les un exemple de complications inutiles que provoque ce
principe quand on veut à tout prix s'y soumettre,
et comment il empêche d'avoir une conception très naturelle et unifiée des
nombres, de faire une science simple et homogène :
Si
on appelle  (ou oméga)
le nombre d'éléments de N,
puisque N, P et I ont
le même nombre d'éléments et qu'en ajoutants
ceux de et I on obtient ceux de N,
on a donc la simple égalité suivante :
(ou oméga)
le nombre d'éléments de N,
puisque N, P et I ont
le même nombre d'éléments et qu'en ajoutants
ceux de et I on obtient ceux de N,
on a donc la simple égalité suivante :  =
=  +
+  .
Et si on calcule normalement avec cette égalité comme
avec tous les nombres réels, on devrait
faire :
.
Et si on calcule normalement avec cette égalité comme
avec tous les nombres réels, on devrait
faire :  -
-  =
=  ,
donc 0 =
,
donc 0 =  .
Ceci
(avec d'autres égalités comme 0 = 1)
exprime une propriété de
l'Univers,
de la plus haute importance, que
j'appelle le Cycle.
.
Ceci
(avec d'autres égalités comme 0 = 1)
exprime une propriété de
l'Univers,
de la plus haute importance, que
j'appelle le Cycle.
Mais
le principe de non-contradiction a
conduit à séparer le domaine des
nombres en différentes
parties (par exemple l'arithmétique
finie est
séparée de l'arithmétique
infinie), et dans chacune
certaines règles des nombres s'appliquent
et pas d'autres. Par exemple, l'arithmétique
infinie accepte des égalités comme
:  =
=  +
+  ou
ou  =
=  + 1,
conformes donc aux propriétés naturelles
de l'infini qu'on
vient de découvrir, mais refuse d'appliquer
les règles communes des nombres que je
viens d'appliquer pour aboutir aux conclusions
simples : 0
=
+ 1,
conformes donc aux propriétés naturelles
de l'infini qu'on
vient de découvrir, mais refuse d'appliquer
les règles communes des nombres que je
viens d'appliquer pour aboutir aux conclusions
simples : 0
=  ou
0 = 1, qui expriment la propriété
de l'Univers que
j'appelle le
Cycle. Le
principe de non-contradiction oblige a zig-zaguer
dans le grand magasin de la vérité et
de la réalité appelé
l'Univers, et à ne sélectionner
que les vérités qui plaisent à ce
principe, et
à appeler "contradictions" les
autres. Et
je répète ceci : La
vraie contradiction, c'est nier
une réalité !
ou
0 = 1, qui expriment la propriété
de l'Univers que
j'appelle le
Cycle. Le
principe de non-contradiction oblige a zig-zaguer
dans le grand magasin de la vérité et
de la réalité appelé
l'Univers, et à ne sélectionner
que les vérités qui plaisent à ce
principe, et
à appeler "contradictions" les
autres. Et
je répète ceci : La
vraie contradiction, c'est nier
une réalité !
C'est
pourquoi il est nécessaire de distinguer
les
paradoxes (les pseudos-contradictions)
des contradictions proprement
dites. Le
problème de la contradiction se
ramène à un
seul problème : la négation ! Le
remède est une toute nouvelle conception
de la négation, à savoir
l'alternation (voir La
Logique alternative, Le
principe d'Alternation),qui
elle est parfaitement conforme à l'Univers et
à ses
propriétés.
Le
schéma "Y" ou l"Arbre" : La
solution, tout simplement...
Ce
que nous enseigne l'affaire de la géométrie euclidienne
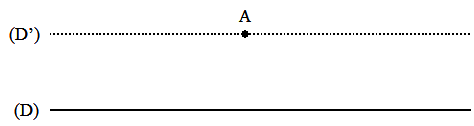
Par le point A
extérieur à la droite (D) il passe une et une
seule droite (D') parallèle à (D).
Le cinquième
postulat d'Euclide.
Vrai, et pourtant le contraire est vrai
aussi !
Mais ce contraire n'est pas aussi évident et intuitif, ce qui peut faire à tort
dire qu'il est faux.
C'est la même prudence qui s'impose maintenant face au fameux principe
de non-contradiction,
énoncé par Aristote, un quasi contemporain d'Euclide.
La question est d'autant plus importante (et même grave !)
qu'elle concerne la notion même de vrai et de faux, donc la notion de vérité
scientifique.
Voici ci-dessous une autre forme de ce cinquième
postulat :
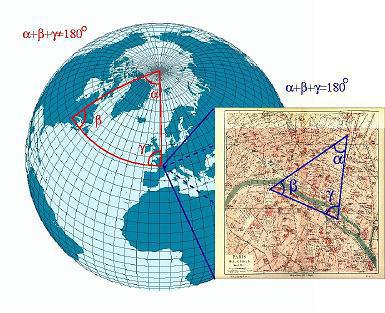
"La somme des angles est 180° ET La
somme des angles n'est
pas
180°".
Contradictoire, et pourtant c'est vrai !
Cette phrase n'est contradictoire que dans chacun des contextes des géométries particulières;
mais dans le contexte général nommé Géométrie,
cette phrase est vraie !
Dans ce contexte global s'expriment simultanément toutes les vérités particulières, tout
et son contraire donc !
sans pour autant que cette simultanéité ne soit une contradiction !
Il est temps d'"abandonner" l'approche contextuelle de la science pour une vision
et une approche
globale des choses !
L'approche contextuelle ou axiomatique (ou "science en pièces détachées",
comme
on le fait actuellement)
ne donne
accès qu'aux vérités particulières.
Les vérités globales et universelles sont interdites par les principes de cette
science,
comme par exemple le principe
de non-contradiction.
Bref, le principe
de non-contradiction est pour la logique et la science en
général
ce que le cinquième
postulat est
pour la géométrie en particulier.
L'enseignement à tirer du problème posé en géométrie est simplement celui-ci
:
"Le contraire de toute vérité est toujours une autre vérité".
Et même plus simple et plus fort : "Tout est
vrai" !
Le contraire d'une vérité donnée (surtout si elle apparaît comme
très évidente)
peut simplement ne pas être évident du tout.
Mais cela ne veut pas dire que c'est faux.
Ou alors il faut donner un autre sens au mot faux...
Une
simple affaire de contextes, de bonne séparation, de
bonne union, de permutation !
Si la science
est un Arbre, par définition on appellera
un contexte une de ses branches.
Si la science est un Ensemble, par définition
on appellera un contexte un de ses sous-ensembles.
Et si la science est l'Univers, par définition
on appellera un contexte un de ses éléments,
c'est-à-dire une chose A quelconque.
Aussi étonnant que cela puisse paraître, c'est
quand on sépare bien les choses,
que l'on découvre toute leur unité,
et donc qu'on les unifie de la plus merveilleuse
des façons. Et réciproquement, c'est quand
on les unifie bien qu'on découvre
enfin ce qui les distingue vraiment, et donc qu'on les sépare de
la meilleure des façons, avec une précision
parfaite ! Mais quand on les sépare mal,
quand on fait des distingos inutiles du
genre "Ne confondons surtout pas porc et cochon" (comme
par exemple la séparation entre "ensemble"
et "collection"
ou entre "égalité" et
"équivalence", etc.),
on les unifie mal aussi,
on élabore une forêt des sciences (faites
de beaucoup de blablablas techniques, sophistiquées
et savants), là où les sciences auraient pu
simplement ne former un seul et magnifique
Arbre !
Et auss,
quand on unifie mal les choses là
où on devrait au contraire bien les séparer,
on engendre beaucoup de confusions qui sont autant de vraie contradictions,
que l'on s'emploie à résoudre méticuleusement avec d'autres
blablablas, mais sans savoir qu'on en est en réalité la cause
! Le meilleur exemple que je peux donner est la notion de
négation. On a posé un mot technique
technique non, appelé le connecteur de négation,
censé modéliser "rigoureusement" la négation naturelle,
telle que nous la faisons dans le langage courant. On en
est venu à dire d'une manière radicale, catégorique et sans
appel, que l'expression "A ET non-A"
est obligatoirement contradictoire ou faux.
Or derrière ce mot non se cache toute
une infinité de
notions scientifiques, qui demandent à être bien séparées,
autant qu'il y a d'entiers naturels ! Tout dépend dans quel
modèle on se place : "modèle à un"
(modèle
universel et unificateur par
excellence), "modèle à deux "
(ou modèle
binaire classique), mais aussi "modèle
à trois",
"modèle à quatre", etc.
La négation
n'est pas du tout la même selon le modèle considéré. Dans
le modèle binaire, il y en a en fait 2, le Oui et
le Non, qu'il falait bien distinguer pour
voir clair dans les choses. Il y en a 6 dans le "modèle à
trois", 24 dans le "modèle à quatre", etc. Cela fait du monde
en fait qui s'appellent négation ou non !
Dans le
modèle à deux (A, B), pour
cette alternation ou symétrie (l'autre étant (B,
A)), B est LE contraire ou LA négation de A,
et
A est LE contraire ou LA
négation de B. Mais une
chose C différente de A et
B n'est ni le contraire de A ni
le contraire de B. Dans ce cas de figure,
C est donc un tiers, qui est est exclu,
puisque le propos porte sur le modèle (A,
B), et qui n'est pas exclu car ce qui est dit de
A ou de B s'applique aussi
à C par symétrie, alternation ou
par substitution. En effet, j'ai dit (A, B) car
il fait prendre deux choses quelconques pour énoncer les
proprités du modèle à deux. Mais j'aurai pu prendre aussi
C pour jouer le rôle de A ou de B,
et le raisonnement serait le même. Et alors c'est C qui
devient
LE contraire de A ou de B,
etc. Autrement dit, pendant que je parlais du modèle (A,
B), le modèle (A, C) existe
aussi, de même que (B, C), (C,
D),
etc. Ce n'est pas parce que j'ai choisi un pour en
parler (parce qu'il faut bien choisir un), que les autres
cessent d'exister. En fait en parlant d'un modèle à deux
quelconque, je parle de tous en même temps ! Par conséquent,
quand je suis en train de dire que B est LA négation de A,
et que C n'est pas le contraire de A,
je suis aussi en même temps en train d'énoncer les vérités
contraires à celles que je dis, sans pourtant me contredire. Quand
on fait le choix d'un contexte pour être au premier plan,
les autres sont masqués ou cachés, ainsi que leurs vérités,
qui sont contraires à celles du premier plan. Mais ce n'est
pas parce qu'ils sont masqués qu'ils n'existent pas, ou que
leurs vérités n'en sont pas. C'est la
philosophie même
de l'alternation.
Dans le
modèle à trois (A, B, C),
la négation d'une
des valeurs est chacune des deux autres ! Par exemple, non-A est B ou C.
Si je limite mon choix de fruits à la pomme,
à l'orange et
au kiwi, je suis dans un modèle à trois (pomme,
orange, kiwi).
Dans ce cas, ne
pas être une pomme (donc non-pomme)
c'est être une orange ou un kiwi.
Dans ce cas mis au premier plan, banane par exemple n'est
pas le contraire de pomme; et pourtant, pour les mêmes raisons
que celles expliquées plus haut, banane est aussi le
contraire de pomme. Et
si j'ajoute le fruit banane pour être
dans un modèle à quatre (pomme, orange,
kiwi, banane), là ne pas être une pomme (ou non-pomme)
c'est être une orange, un kiwi ou
une banane. Et dans le modèle infini,
où les valeurs de vérité sont toutes les choses, donc tous
les
éléments de l'Univers, ne
pas être une pomme c'est être ces autres fruits, ou un humain,
ou caillou, ou le soleil,
etc. Mais comme toujours, le contraire de ce que je dis est toujours
vrai aussi, par alternation (ou permutation ou symétrie).
Bref, là
où je sépare bien les choses,
là où je distingue avec grande précision les contextes et
les différentes alternations (ou permutaions ou symétries),
là aussi apparaît l'union des
choses, le fait que tout ce que je dis d'une chose donnée
A est vrai aussi pour toute autre chose B !
Deux choses A et B sont
tantôt opposées et contraires,
et tantôt elles sont la même chose ! Il n'existe qu'une seule
négation notée non, et il
en existe aussi toute une infinité. A et non-A sont
tantôt négation l'une de l'autre,
et donc "A ET non-A" est contradictoire,
et tantôt A et non-A ne
se nient plus, et donc "A ET non-A" n'est
plus contradictoire. Tout dépend du contexte, mais dans le
plus grand des contextes, l'Univers, tout
finalement s'unifie, tout est un attribut du
seul et même
Univers, tout et son contraire est vrai.
L'arbre
de la réconciliation...
Ce qui
est paradoxal avec le principe
de non-contradiction, c'est qu'on a avec ce principe
au moins une preuve de l'existence de situations montrant
que le contraire de ce principe peut être
vrai aussi !
L'exemple
historique et très parlant de cette situation
est fourni par l'affaire de la géométrie euclidienne
(appelons-là ici GE) et la géométrie non
euclidienne (appelons-là GNE). L'une affirme un énoncé A,
par exemple ce qui est appelé le cinquième postulat
d'Euclide" (qui dit que la somme des angles d'un triangle
est de 180°), et l'autre affirme le contraire; autrement
dit, il est tout à fait possible de construire une géométrie
qui nie le cinquième postulat, qui affirme donc non-A
(c'est-à-dire que la somme des angles d'un triangle
est différente de 180°). Il revient exactement au
même de dire que A et non-A sont respectivement des vérités
de deux réalités séparées GE et
GNE, que de dire que l'énoncé "A ET non-A" (dit "contradictoire")
est une vérité dans une réalité nommée
G (pour géométrie), qui est simplement le réunion
de GE et GNE (c'est-à-dire G = GE U GNE), ou une réalité G
incluant cette réunion (GE U GNE) comme sous-réalité,
et donc aussi GE et GNE comme sous-réalités encore
plus petites. En effet, la géométrie peut tout
aussi bien englober d'autres questions et problèmes
que ceux concernant les axiomes (ou postulats d'Euclide). En
d'autres termes, la question de la géométrie
peut tout aussi bien se poser autrement que de savoir
si oui ou non elle est euclidienne, ce qui est d'ailleurs
le cas.
Cet exemple de la géométrie euclidienne est
particulièrement instructif sur cette question de la
contradiction. Dans chacune des sous-réalités
(ou contextes) GE et GNE, l'énoncé "A ET
non-A" est une "contradiction", car chacun des
contextes accepte une des deux parties contradictoires, et
pas l'autre. Mais dans la réalité supérieure
G (qui est "au-dessus de la mêlée" en
quelque sorte), ce débat du genre "Vrai ou Faux
?" ou "Pour ou Contre ?" ou "Oui ou Non
?" ne se pose plus. C'est l'espace de "pacification" du
débat, le contexte de "réconciliation" ou
d'"unification" des deux aspects contraires, la réalité où il
apparaît que "A ET non-A" n'est plus une "contradiction" mais
une simple vérité, bref le lieu où l'on
apprend cette très simple vérité : "Le
contraire de toute vérité est toujours une autre
vérité" ! Ce contexte est ce que j'appelle
un contexte d'alternation, c'est-à-dire un contexte
où la contradiction cesse d'être négative
pour devenir positive, où l'absurdité devient
une autre vérité, une autre logique. Les deux
aspects contradictoires deviennent de simples propriétés
d'une même réalité G, autrement dit A et
non-A sont bel et bien des attributs de cette seule et même
chose nommée G. Autrement dit encore, c'est vrai que
G possède l'attribut A, et c'est vrai aussi que G ne
possède pas cet attribut. C'est pourquoi donc face au
principe de non-contradiction, la réponse normande "Oui
ET Non" se justifie bien !
Cet exemple historique de la géométrie est d'autant
plus intéressant que non seulement qu'il contribue à faire
l'anatomie de la contradiction, mais surtout il fournit la
méthode simple de résoudre n'importe qu'elle
situation contradictoire "A ET non-A". Cette contradiction
est toujours une vérité d'un certain contexte
C, ayant deux sous-contextes séparés C1 et C2,
où respectivement A et non-A est vrai, et où chacune
des deux vérités exclut son contraire. Les contextes
C1 et C2 ne sont pas séparés au sens le plus
absolu, c'est-à-dire qu'ils ne sont pas disjoints ou "parallèles",
sans rien de commun. Mais ils ont justement C en commun, qui
les unifie, mais aussi un autre contexte minimal commun C3
(au pire vide) qui rassemble les énoncés à la
fois vrais dans C1 et C2, comme le montrent le schéma
ci-dessous :
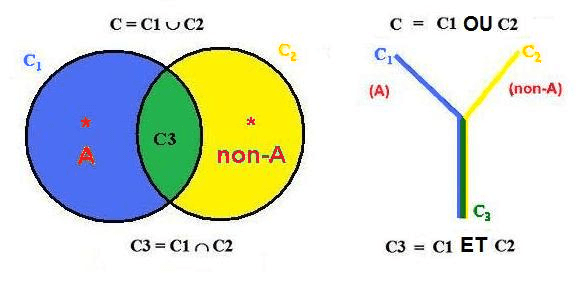
Schéma
"Y" ou "Arbre" :
Il n'y
a contradiction que si A et non-A se
retrouvent en (C1-C3) ou (C2-C3).
Ce schéma montre ce que j'appelle la structure élémentaire
de l'Arbre ou structure "Y". C'est la clef de la
solution de toutes les situations "contradictoires",
mais aussi de la logique fondée sur l'alternation, le
contraire du principe de non-contradiction, qui peut s'énonce
ainsi : "Le contraire de toute vérité est
toujours une autre vérité", ou : "Une
chose et son contraire peuvent être vraies à la
fois". Le contexte ou ceci est possible est ici C. C'est
dans les sous-contextes C1 et C2 qu'on peut parler de "contradiction",
et plus exactement dans les parties qui les différencie
strictement, à savoir (C1 - C3) et (C2 - C3), notés
C'1 et C'2. C'est dans ces sous-contextes stricts que les énoncés
contraires A et non-A sont respectivement vrais. Le contexte
C3 est appelé le "tronc" de l'Arbre C, et
C'1 et C'2 sont quant à eux appelés les "branches" de
l'Arbre C. Le contexte C3 est très important car c'est
lui qui contient les propriétés générales
(les énoncés communs) à C1 et C2, qui
caractérisent à la fois C, C1 et C2. Dans l'exemple
de la géométrie plus haut, c'est C3 qui les conditions
ou les propriétés générales qu'une
chose doit posséder pour qu'on l'appelle une "géométrie",
et qui distingue donc ce domaine des autres : "algèbre", "arithmétique",
etc. Dans cet exemple donc, tout domaine ou contexte qui possèdent
les propriétés minimales (donc les plus générales)
définies par C3, est une géométrie. Le
tronc C3 est donc appelé aussi la "définition" de
l'Arbre C. Ensuite, l'Arbre se différencie par ses branches,
qui sont C1 et C2 au sens large, et C'1 et C'2 au sens strict.
C'est cette partie-là qui fait la spécificité de
chacun des contextes, là où les branches de l'Arbre
divergent à partir du tronc commun.
Comme on le voit, le principe d'alternation,
bien qu'étant
le contraire du principe de non-contradiction, ne l'exclut
pas. Celui-ci est simplement un sous-principe de l'alternation,
qui précise très exactement son domaine de validité et
ses limites qui existent. L'alternation instaure une structure
de la science dans lequel le langage habituel de l'Arbre (quand
on dit par exemple que tel domaine est une branche de tel autre
domaine) prend tous son sens (voir aussi l'Arbre de la Science).