Le Principe d'Alternation
ou Loi de la Théorie de l'Universalité
ou Loi de la Physique de toutes les choses
ou Loi de l'Invariance de l'Univers TOTAL
ou Loi de l'Univers-Dieu

L'Univers TOTAL, l'Univers-Dieu, est l'Ensemble de toutes les choses; par conséquent :
Toutes les choses existent dans l'Univers TOTAL,
toutes les situations existent, toutes les combinaisons existent, toutes les configurations existent,
tous les cas de figure existent, toutes les possibilités existent, toutes les alternatives existent.

L'Univers TOTAL, l'Univers-Dieu, est donc la chose qui possède tous les attributs,
et aussi exactement les contraires des mêmes attributs.
Donc dans l'Univers TOTAL, TOUT est possible !
Tout est vrai dans dans l'Univers TOTAL, et le contraire de tout est vrai aussi;
il n'y a que dans un contexte donné, ou selon un certain point de vue donné, qu'une chose est fausse.

L'Univers TOTAL, l'Univers-Dieu, est l'Ensemble de toutes les choses; par conséquent :
Rien ne se perd, rien ne se crée dans l'Univers TOTAL, mais tout se transforme;
les choses se transforment les unes en les autres, elles ALTERNENT, elles permutent leurs rôles.

Une chose donnée évolue sans cesse dans l'Univers TOTAL, l'Univers-Dieu;
elle devient tour à tour toutes les autres choses, elle passe par tous les états,
elle parcourt tout le Cycle de l'Univers TOTAL, puis elle revient à un moment ou à un autre dans son état initial.
Les choses ne se perdent et ne se créent que dans un sous-contexte donné de l'Univers TOTAL;
mais quant à l'Univers TOTAL lui-même, quant à l'Univers-Dieu,
il reste toujours EGAL à lui-même, il est INVARIANT, IMMUABLE, CONSTANT...

Qu'est-ce que l'Alternation ?.
--> Le paradigme de la Science Nouvelle
--> L'Univers TOTAL est la clef de toute l'affaire
--> Le paradigme d'ALTER
--> Table de Négation et Table d'Alternation
--> Incroyable et pourtant vrai !

Le principe de la Physique de toutes les choses
--> L'Alternation, le principe de la Physique Nouvelle
--> Paradigme du Cycle, nouvelle conception des nombres
--> Paradigme du Modèle, paradigme de la Fractale
--> Comme le courant alternatif
--> Contextualité (Relativité) et Universalité (Absoluité)

Pour aller plus loin...
--> L'Affirmation et la Négation en toute rigeur.
--> Multiplication des sens, multiplication naturelle
--> La troisième valeur de vérité et la physique
--> Il y aurait encore beaucoup à dire !

Qu'est-ce que l'Alternation ?

Le paradigme de la Science Nouvelle

La Science de l'Existence ou Science Nouvelle a pour fondement l'Univers TOTAL, l'Ensemble de toutes les choses (voir Science de l'Univers, Physique de toutes les choses, et Chose, Existence, Ensemble). De la définition de cet Univers il découle immédiatement un Théorème trivial : "Toute chose existe dans l'Univers TOTAL" ou "TOUTE chose existe dans l'Ensemble de toutes les choses".

Ce principe n'est qu'une autre manière de parler du Théorème de l'Existence, qui dit simplement : "Toute chose existe". Dit ainsi, on ne mesure pas toute la force et l'extraordinaire puissance du théorème. Et surtout, on ne se rend pas compte que ce simple énoncé signifie aussi toute une autre logique scientifique (la logique alternative), qui est tout le contraire de la logique scientifique et de tous les paradigmes actuels (voir La fin de la science aristotélienne).

A la rigueur, on n'accorderait volontiers (et encore ce n'est pas sûr) qu'un simple intérêt philosophique ou théologique au Théorème de l'Existence, car qui dit que "Toute chose existe" dit aussi immédiatement que Dieu existe. Et alors les grands athées devant l'Eternel et les champions de la Négation (comme il y en a beaucoup par exemple ici) diront : "En admettant même Dieu existe ou que son existence soit prouvée, et alors, ça change quoi ?"

C'est donc pourquoi il est très important de comprendre ce que veut dire au juste le Théorème de l'Existence et surtout ce qu'il change. Et il change tout simplement TOUT ! La science et le monde avec ce théorème n'a plus rien à voir (ou presque) avec la science et le monde sans ce théorème. C'est en tant que Loi de l'Univers que non seulement on comprend ce que veut dire au juste le Théorème de l'Existence, mais que l'on découvre du même coup toute la nouvelle logique scientifique lui est associée, toute la nouvelle vision de l'Univers qu'il est.

Comme Loi de l'Univers, je donne à ce théorème le nom de Principe d'Alternation ou simplement Alternation. La raison et l'origine du mot "alternation" sera présentée plus loin, car elle mérite d'importantes explications. Il suffit pour l'instant de dire que l'alternation s'oppose radicalement à la négation. Elle inaugure la logique alternative (celle de l'alternation donc) opposée à l'actuelle logique, qualifiée de logique négative (celle de la négation donc).

Quant au mot "principe" tel que je l'utilise, il est comme quand quelqu'un dit : "Je vais vous expliquer le principe de cette machine"; autrement dit la manière dont fonctionne cette machine, ou encore sa logique. L'appellation "principe d'alternation" a pour but d'indiquer qu'il s'agit du principe même du fonctionnement de l'Univers en tant que Machine ou Organisme, il s'agit de la logique même de l'Univers. Car c'est bien une Machine que l'Univers est, la Machine de toutes les machines. Et c'est aussi d'un Organisme qu'il s'agit d'un Etre vivant, la l'Etre suprême, l'Univers-Dieu.

Le Principe d'Alternation révèle donc aussi la nature profonde de l'Univers, ce qu'il EST, pourquoi il EST, comment il EST, comment il fonctionne. C'est en tant que tel que cette Loi de l'Univers est le Théorème de l'Existence, le Théorème de l'Etre. Avec ce principe, c'est plus que la science du comment des choses, mais c'est aussi enfin la science du pourquoi des choses, de la nature des choses, de leur ETRE !

L'Univers TOTAL, la clef de toute l'affaire !

Le Principe d'Alternation (ou Théorème de l'Existence) prend divers noms selon son aspect que l'on veut mettre en évidence. Voyons les plus fondamentaux d'entre ces aspects :

1) Loi de la Physique de toutes les choses ou Loi de la Théorie de l'Universalité ou simplement Loi d'Universalité :
"L'Univers TOTAL est l'Ensemble de toutes les choses" ou simplement "L'Univers est l'Ensemble de toutes les choses".

En mathématiques comme en physique, les propriétés d'une chose donnée ainsi que les théorèmes et les lois qui la concernent dépendent étroitement de sa définition. De ce point de vue, l'affaire que nous examinons n'est même pas un théorème, une loi ou un principe au sens classique de ces termes, mais quelque chose de plus fondamental que tout cela, à savoir une simple affaire de définition de l'Univers. En somme, "Dites-moi de quelle chose vous parlez et je vous dirai comme elle marche".

2) Loi d'existence de l'Univers TOTAL ou simplement Loi de l'Univers TOTAL ou Loi de l'Univers-Dieu :
"L'Ensemble de toutes les choses existe" ou "L'Univers TOTAL existe" ou simplement "Le TOUT existe".

Une simple variante de la formulation précédente du Principe d'Alternation. Cette variante a simplement pour but de mettre en évidence le subtil problème philosophique soulevé par l'Univers TOTAL ou le TOUT, au sens le plus absolu du terme. Elle répond à ce simple souci : il ne suffit pas de définir une chose pour que cette chose existe. Car je peux par exemple définir un adamacent comme étant "Un humain ayant une taille de 100 mètres ou plus". De là on peut déduire beaucoup de choses, qui sont autant de lois concernant cette chose. Par exemple qu'un adamacent peut faire des pas de 10 mètres ou peut soulever une Twingo. Mais tout cela ne dit pas qu'un adamacent existe.

C'est toute la subtilité du problème, auquel répond cette deuxième forme du Principe d'Alternation, la question de l'existence de l'objet dont ce principe décrit la nature et le fonctionnement. Cet objet, appelé l'Univers TOTAL, est défini comme étant l'Ensemble de toutes les choses, exactement comme j'ai défini un adamacent. Comme pour ce dernier, on doit répondre à la question de son existence, pour que l'on ne passe pas le temps à discuter sur une chimère. Si la première formulation est juste une simple définition de l'Univers TOTAL ou de ce qu'il faut entendre par le mot "Univers", c'est ici que commence véritablement le théorème, la loi ou le principe. Cela consiste à dire qu'un tel Univers TOTAL existe, ou que ce que nous appelons "Univers" et qui englobe nous-mêmes, les choses qui nous entourent, notre planète, notre système solaire, notre galaxie la Voie Lactée, etc., est l'Univers TOTAL défini comme l'Ensemble de toutes les choses.

Le paradigme d'ALTER

Et maintenant, commençons par définir l'Alternation elle-même, et avec elle tout le cortège des nouvelles notions qui lui sont intimement associées, et même qui souvent lui sont simplement équivalentes. Mais il s'agit aussi de redéfinir beaucoup d'importantes notions scientifiques actuelles, qui prennent toute une autre signification avec le concept d'alternation, comme la très importante notion de négation, fondamentale en logique et dans le raisonnement.

Pour définir simplement l'Alternation, je dirai que c'est tout raisonnement ou toute situation qui implique directement ou indirectement le mot AUTRE, en latin ALTER. Les notions courantes comme "alternance", "alternatif", "alternative", etc., sont donc des mots du langage de l'alternation, ne serait-ce simplement parce qu'ils contiennent le mot clef de l'alternation, à savoir AUTRE ou ALTER, comme aussi dans des mots comme "autrui", "altruisme". Donc les expressions très courantes comme "L'un l'autre" ou "L'un et l'autre" (comme quand Jésus dit : "Aimez-vous les uns les autres"), sont des expressions d'alternation. Et aussi nombre d'expressions très habituelles, qui ne contiennent pas explicitement le mot AUTRE ou ALTER, mais dont l'idée y est, et plus précisément l'idée d'alternance, comme par exemple : "vice-versa", "réciproquement", "inversement", "à l'opposé", "contraire", "contrairement", etc. Ce sont des termes d'alternation, ici précisément son cas particulier que j'appelle l'alternation 2, le cas où l'on se trouve devant deux alternatives A et B.

Dans le cas de deux alternatives A et B, si A est appelée "L'Une" alors B est appelée "L'Autre", et vice-versa; car le choix inverse est vrai aussi, on a deux possibilités (ou alternatives) parfaitement équivalentes de choisir celle des deux choses A et B qui va être appelée "L'Une", et c'est-à-dire qui va être nommée la première; il en résulte donc celle qui va être appelée "L'Autre", et donc qui sera nommé la seconde. Dans l'absolu donc, les deux possibilités existent et sont aussi vraies l'une que l'autre ! Cette équivalence va rendre A et B parfaitement symétriques, ce qui signifie que tout ce qu'on va pouvoir dire de "L'Une" des deux choses va par symétrie du raisonnement être vrai aussi pour "L'Autre". Ce point est capital dans la pensée de l'alternation, qui va radicalement la différencier de la philosophie actuelle où l'on perd très souvent de vue cette symétrie du raisonnement ! Quand donc on fait un choix donné ou que l'on se donne une convention, on oublie que toutes les autres conventions existent et sont des vérités alternatives, des possibilités ! Il faut faire ce que j'appelle le "Test de l'extraterrestre" ou découvrir que toutes les autres alternatives ou possibilités.

Ce premier exemple d'alternation 2 (le cas "L'Un et L'Autre") nous a permis de présenter quelques unes des notions base de très grande importance dans le langage de l'alternation : Un, Autre ou Alter, Choix, Alternative ou Possibilité, Equivalence, Symétrie. D'autres notions de très grande importance et puissance, qui font partie du langage de l'Alternation, et qui constituent tout un nouveau sens d'importantes notions actuelles, seront découvertes au fur et à mesure de l'exposé de ce concept nommé l'Alternation. Définissons maintenant ce concept dans toute sa généralité.

Plus techniquement, pour tout entier naturel n donné, on appelle alternation n toute liste ordonnée de n choses distinctes absolument quelconques (A1, A2, A3, ..., An), notée ainsi. Et une alternation infinie est par définition une liste de toutes les choses de l'Univers ou simplement Univers ! car ce sont ses propriétés inconnues jusqu'ici (et impossibles à connaître) par la science faite la Négation, que je suis simplement en train de décrire dans le langage de l'alternation, qui est simplement la langage de l'Univers. Et en fait l'alternation infinie : (A0, A1, A2, A3, A4, A5, A6, A7, ...), qui consiste à considérer une liste infinie ordonnée de choses indexées par les nombres entiers naturels (ou tout simplement la liste de ces entiers naturels eux-mêmes !), suffit plus qu'amplement pour découvrir tout ce que nous devons découvrir. Toutes les alternations sont des sous-alternations de celle-là, qu'on peut donc appeler l'Alternation !

Je viens donc de définir l'Alternation de deux manières parfaitement équivalentes : la première, la plus simple et la plus intuitive est toute situation qui implique directement ou indirectement le mot AUTRE ou ALTER, appelé le connecteur logique d'alternation, et qui va remplacer maintenant connecteur logique de négation non, car le nouveau connecteur est infiniment plus fécond et plus puissant. Et la seconde définition est purement technique : une alternation est simplement une liste ordonnée (A1, A2, A3, ..., An) de choses, finie ou infinie, éventuellement réduite à une seule chose A, alternation 1 notée (A). ou même à une liste vide, notée alors ().

Très intuititivement, cette définition technique signifie simplement qu'on s'est donné un certains nombres n (éventuellement infini) de choses (A1, A2, A3, ..., An), et on s'astreint par là à ne faire un choix (notion très importante, comme aussi la notion de décision, car c'est nous qui décidons...) que parmi ces n choses, appelées par définition les alternatives ou les possibilités. C'est le sens très précis qu'aura le mot possibilité dans le langage de l'alternation, à savoir qu'un simple synonyme d'alternative, donc une possibilité parmi un certain nombre n donné, qui définit l'alternation en question, l'alternation n appelée aussi le cycle n. Et c'est ce qu'il faut aussi entendre par "nombre n" ou encore "permuation n", "modèle n", "fractale n", "symétrie n", "équivalence n", etc. Tous ces termes et d'autres sont parfaitement synonymes d'"alternation n" de le langage de l'alternation; seulement selon le contexte et l'angle sous lequel on veut examiner une alternation n donnée ou sa propriété étudiée, un terme sera préféré à un autre. Mais il importe de savoir qu'on parle toujours d'une seule et même chose, sous ses différents aspects. Dans la pensée de l'alternation, il importe de savoir par exemple que Pile et Face sont deux aspects d'une même pièce de monnaie, deux angles différents sous lequel voir la même pièce et dire ce qu'elle est, et aussi que Pile n'est qu'une autre manière de dire Face et vice-versa, plutôt que voir Pile et Face comme deux choses complètement séparées, qui n'ont aucun lien l'un avec l'autre. Dans ce cas, l'un des mots peut par exemple appartenir à la mathématique et l'autre à la physique, ou à la biologie ou même à la religion !, et on peut croire qu'on parle de choses différentes qui n'ont rien à voir l'une avec l'autre, alors qu'elles ne sont finalement que la même chose ! L'alternation est donc en train de réaliser une unité entre différents termes scientifiques, et cette unité va même au-delà de la science dans son état actuel, et fait voir que des notions religieuses (le Diable par exemple) ne sont que d'autres mots pour dire la même chose que des mots en science (la notion Négation par exemple, liée à la question du Vrai et surtout du Faux, comme on va le montrer maintenant).

Table de Négation et Table d'Alternation...

Voici ce qu'on appelle traditionnellement la table de vérité du connecteur de négation non :

Table du connecteur de négation NON :
Faux = non Vrai et Vrai = non Faux.
Il importe de préciser que ceci ne s'applique qu'à un objet p
censé être seulement la valeur de vérité Vrai ou Faux,
ou un énoncé dont on indique ainsi la valeur de vérité de NON p connaissant la sienne.
Mais l'alternation va bien au-delà de ces considérations restrictives,
et au-delà de cette conception de la vérité (celle de la logique classique) et de ses préjugés...
L'alternation ne retient que ce que veut vraiment dire cette table,
tout simplement une alternance entre deux choses,
ici nommées a priori Vrai et Faux, mais qui peuvent être AUTRES que cela !

Nous pouvons maintenant définir la nouvelle notion de négation, celle de l'alternation. C'est l'alternation 2, notée (A, B), qui va permettre de définir cette notion. Par définition, B sera appélé le contraire de A ou l'alternative de A, et sera noté : alter A. Et réciproquement, A sera appelé le contraire de B ou l'alternative de B, et sera noté : alter B. Donc : B = alter A et A = alter B, ainsi que le montre maintenant la table du connecteur ALTER :

Table du connecteur d'alternation ALTER :
B = alter A et A = alter B.
Nouvelle définition de la notion de contraire ou de négation;
maintenant, dire que les choses A et B sont la négation l'une de l'autre,
ou dire que A et B sont contraire l'une de l'autre,
signifie tout simplement qu'on se place dans une situation
où l'on ne se donne que ces deux choses comme alternatives ou possibilités de choix,
et donc que l'une est l'alternative de l'autre et vice-versa.

Cette table donne les propriétés nécessaires et suffisantes, pour qu'une application T d'un ensemble ordonné à deux éléments (A, B) dans lui-même puisse être appelé une négation. La table classique du connecteur NON et celle du connecteur d'ALTER présentent cette propriété nécessaire et suffisante, et donc cela suffit pour que les deux connecteurs soient notés non et appelés des négations. Mais la similitude s'arrête-là, on s'en tient à ce que dit cette table, à savoir qu'on alterne simplement les deux choses A et B, c'est-à-dire : A devient B et B devient A. C'est tout. Cette table ne dit rien d'autre à part ça, elle ne nous dit pas par exemple que A est Vrai que B est Faux, ou vice-versa; ou qu'il est impossible que les deux soient Vrais en même temps (principe de non-contradiction*), etc.

On note au passage que dans le langage de l'alternation, les termes "alternative" et "possibilité" sont parfaitement synonymes. Une chose A est "possible" si elle constitue une alternative, c'est-à-dire s'il existe une alternation donnée qui la propose parmi ses alternatives ou ses possibilités. Ce sont les bases mêmes de la notion d'alternation, et le verbe de la situation est le verbe ALTERNER, qui veut dire permuter les rôles des différentes alternatives ou choses en présence.

C'est ici que se présente toute la différence entre l'alternation et la négation. On va découvrir avec l'alternation pourquoi tout est vrai, tout est possible, tout existe dans l'Univers. Une chose n'est fausse ou impossible que dans un contexte donné, dans un sous-ensemble de l'Univers, ou relativement à une chose donnée dans l'Univers. Et il n'y a que dans un contexte donné ou à un certain point de vue donné qu'on peut dire qu'une chose A n'existe pas. Mais dans l'absolu, c'est-à-dire donc dans le grand Univers tout entier, la chose A existe toujours (Théorème de l'Existence), on cesse d'exister ici pour exister ailleurs. Une chose qui n'est pas vraie d'un point de vue est toujours vraie d'un autre. Et ce qui n'est pas possible d'un point de vue ou dans un contexte donné est toujours possible d'un autre.

Le mot alternation a justement été formé initialement pour signifier "alter négation" ou "autre négation", par opposition à la conception actuelle de la négation. Avec la négation actuelle on NIE les existence ou les choses, sans proposer une alternative (ou possibilité) d'existence pour la chose niée. Elle détruit purement et simplement les choses, sans les recréer sous une autre forme.

Par contre, avec l'alternation, on ALTERNE entre les choses; on passe d'une chose à une autre, et vice-versa, on permute les choses, on fait bouger les choses, on fait varier les choses, on fait évoluer les choses, on change les choses, on transforme une chose en une autre, on recycle les choses, etc. "Rien ne se perd, rien ne se crée, mais tout se transforme dans l'Univers".

L'alternation est le principe même du fonctionnement de l'Univers dont nous faisons partie. On voit les choses comme on raisonne, comme on nie ou comme on affirme. Si on dit par exemple qu'une chose A n'existe pas (Dieu par exemple...), c'est ainsi qu'on la voit, ou plutôt qu'on ne la voit pas... D'où toute l'importance de clarifier la négation, pour une bonne vision des choses.

Incroyable et pourtant vrai !

L'alternation change complètement l'approche de la science, la notion de vérité, de possibilité, et fait découvrir des vérités sur l'Univers, que la négation ne peut que déclarer impossibles. Voici un petit exemple banal, et la lecture des choses telle qu'on la fait maintenant avec le puissant concept d'alternation. Il sera suivi ensuite d'énoncés inconcevables ou impossibles avec la négation, qui donnent le ton de la nouvelle vision des choses avec le nouveau paradigme scientifique.

L'Alternation est le principe même de la Physique de toutes les choses,
le principe du fonctionnement même de l'Univers.
Un Cône de révolution est un exemple d'objet alternatif (c'est-à-dire obéissant à l'Alternation).
Un mouvement de rotation est un mouvement alternatif ;
le Cône peut être décrit comme un Triangle en rotation, qui le génère ainsi par alternation.
Un mouvement de va-et-vient est un mouvement alternatif;
le même Cône peut être décrit comme un Cercle (ou Disque) faisant mouvement vertical de va-et-vient (un mouvement alternatif),
un Disque dont le rayon diminue quant il descend et augment quand il monte.
Le Triangle peut être décrit comme un Segment qui fait un mouvement alternatif de type va-et-vient,
dont la longueur diminue quand il descend et augmente quand il monte;
il généère ainsi le Triangle qui par rotation génére le Cône.
De la même façon, un Disque est généré par un Segment en rotation,
et lui-même génère le Cône par un moment de translation alternatif.
Et le Segment est généré par un Point en mouvement alternatif, etc.

L'Alternation permet donc de comprendre qu'un Cône est à la fois
un Point, un Segment, un Disque, un Triangle, etc.
Et aussi l'Alternation permet de comprendre que le Point est tout cela à fois,
car c'est lui qui par alternation génère toute cette diversité de formes.
C'est ainsi que l'Univers, par alternation, génère toute la Diversité des choses.
Incroyable mais vrai !
Le TOUT, l'Univers, est pourtant aussi la plus petite des choses, la Particule !
La Particule génère tout l'Univers, qui est une Particule qui génère tout l'Univers, et ainsi de suite.
C'est tout simplement la structure de l'Univers fractal;
Incroyable mais vrai !

Dans un monde seulement en deux dimensions, on sait ce qu'est un Triangle plein ou un Cercle plein (ou Disque). Mais, à moins de fonctionner avec l'alternation, on ne peut pas concevoir un objet A qui soit à la fois un Triangle et un Cercle, c'est-à-dire qui réponde au signalement "Triangle ET non-Triangle"; c'est ce qu'on appellerait dans ce monde un objet "contradictoire" ou un objet "impossible"; Mais nous savons dans notre monde que cet objet existe et nous l'appelons un Cône. C'est ainsi que dans notre monde nous quailifions de contradictoires ou d'impossibles des réalités,à cause tout simplement du fait qu'on fonctionne avec la négation au lieu de le faire avec l'alternation. Découvrons avec l'alternation l'Univers tel que nous n'aurions jamais pu le comprendre avec la négation :

- "Le contraire de toute vérité est toujours une autre vérité." (Enoncé standard du principe d'alternation)
- "Tout ce qu'on peut dire sur une chose A, est vrai pour toute autre chose B !" (Loi des modèles)
- "Tout ce qu'est une chose A, toute autre chose B l'est aussi, ou peut le devenir." (Loi du Cycle)
- "Deux choses A et B, si différentes paraissent-elles dans un contexte donné, sont finalement la seule et même chose." (Loi de l'Univers fractal numéro 1)
- "Malgré les apparences, toute chose A est une version de l'Univers tout entier !" (Loi de l'Univers fractal numéro 2)
- "L'Univers tout entier est aussi chacun de ses éléments." (Loi de l'Univers fractal numéro 3)

Incroyable, et pourtant vrai ! En effet, il suffit de réfléchir un tout petit peu pour s'apercevoir qu'après tout, il fallait s'attendre de la part de cette chose qu'est l'Univers (je parle du grand TOUT, donc unique en son genre), d'en voir de "toutes les couleurs" ! Ce n'est pas si surprenant finalement que cette chose si spéciale (et unique) qu'est l'Univers ne peut que posséder des propriétés exceptionnelles.

Ne dit-on pas : "Il faut de tout pour faire un monde ?" Et reconnaissons qu'on énonce cette magnifique vérité quand on se trouve devant des choses plutôt étranges, tout le contraire de ce qu'on pouvait imaginer ou considérer comme "normal". Alors on lâche : "Il faut de tout pour faire un monde". C'est encore plus vrai pour l'Univers : "Il faut de TOUT pour faire l'Univers". Autrement dit donc, dans l'Univers, il y a de tout et aussi le contraire de tout ! Sans cela, l'Univers ne mériterait pas sa définition d'être le TOUT. Mais dire que l'Univers est fait de TOUT (donc de tout et du contraire de tout), c'est dire : "Le contraire de toute vérité est toujours une autre vérité."

Le principe de la Physique de toutes les choses

L'alternation, le principe de la Physique Nouvelle

Les connecteurs de l'alternation sont dynamiques

L'alternation fait peu de place à l'abstrait. Tout dans le concept d'alternation est physique, concret ! La logique de l'alternation est une logique physique, les connecteurs NON, OU, ET, etc., ont une signification physique et dynamique, et l'équivalence logique (), doit être vu aussi comme un signe indiquant un mouvement de va-et-vient, une oscillation entre deux états, par exemple "Haut" et "Bas", "Ouvert" et "Fermé", etc., ou comme le courant alternatif :

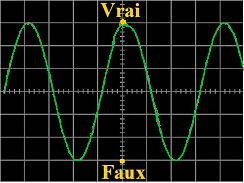
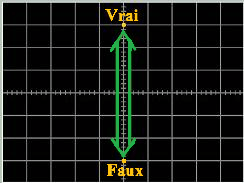
Figure 1 : La vision physique et oscillatoire de l'équivalence logique

C'est ainsi qu'il faut voir les équivalences logiques comme : A non-A, ou comme : Vrai Faux. On passe d'une valeur de vérité à l'autre : "si A est vrai, alors il doit devenir faux, et si A est faux, alors il doit devenir vrai". Dans une logique abstraite et statique, le verbe être est lui aussi statique, l'état est statique, et alors cette équivalence logique se lirait : "si A est vrai, alors EST faux, et si A est faux, alors il EST vrai". Et on appelle cela alors une contradiction, le type du paradoxe de Russel ou du paradoxe du menteur. Mais dans une logique concrète et dynamique, celle de l'alternation, le verbe être est lui aussi dynamique (le verbe devenir), les états sont dynamiques, on passe d'un état à un autre, d'une forme d'être à une autre forme d'être, d'un contexte à un autre, etc. Bref c'est la logique de l'Univers, de la Réalité, de la vie, des êtres, comme les êtres humains par exemple ! Et alors il n'y a plus de contradiction.

Objets alternatifs de type "A ET non-A"

Figure 2 : Le Cône est "Cercle ET Triangle", et l'Univers est TOUT...

Des êtres qui vivraient dans un monde en deux dimensions connaîtraient le cercle (disque) et le triangle (plein), mais auraient du mal à imaginer un objet qui soit à la fois un cercle et un triangle ! L'objet "Cercle ET Triangle" (donc un objet "Cercle ET non-Cercle") est pour eux un objet contradictoire. Mais la troisième dimension résout le problème, dans un monde en trois dimension existe un cône de révolution, qui suivant comme il est projeté dans un espace à dimension, peut apparaître comme un disque et comme un triangle. L'alternation permet d'avoir une autre lecture, une autre compréhension de l'Univers, de découvrir des objets de type "Vrai ET Faux", qui sortent des limites étroites du principe de non contradiction et du principe du tiers exclu. Ces objets sont dit "alternatifs", car ils requièrent une logique d'alternation pour lever contradiction qu'ils présentent et qui n'est donc qu'apparente. Voici un autre exemple d'objet alternatif :

Figure 3 : Le Gris est "Blanc ET Noir", et l'Univers est TOUT...

Une plaque rectangulaire est blanche au recto et noire au verso. Quand la plaque rectangulaire tourne suivant un axe vertical, cela donne un objet cylindrique de couleur grise, un objet alternatif "Rectangle ET Cercle" (le Cercle venant ici de la rotation). Sur ce plan, cet exemple rejoint le précédent.

Dans un monde où les êtres ne connaissent que deux couleurs, le Noir et le Blanc, ils ne connaissent donc pas de troisème couleur, comme le Gris par exemple, qui serait à interpréter comme "Noir ET Blanc", exactement comme un métisse, dont un parent serait blanc et l'autre noir, présente les caractères à la fois blanc et noir. On dit souvent de Barack Obama qu'il est un "noir de mère blanche"; mais il est donc aussi un "blanc de père noir"... comme mes enfants. Désolé pour les psychologies lepennistes ou subtilement racisme, pour lesquelles on n'est que noir dès qu'on présente le moindre caractère noir... L'alternation c'est aussi aussi la fin de ce genre d'esprit (surtout blanc..), qui refuse qu'on soit "Blanc ET non-Blanc" (voir Là où se cache le Diable). C'est la face cachée du principe de non-contradiction*, le principe de prédilection d'une certaine civilisation, de son rationnalisme, de sa science...

Paradigme du Cycle, nouvelle conception des nombres

Figure 4 : L'alternation implique une nouvelle conception des nombres, celle du Cycle (voir la vidéo L'Algèbre du Cycle)

Diverses très importantes notions sont associées à l'alternation, comme par exemple la notion de Cycle et de Modèle. Elle change complètement la notion de nombre, qui devient une notion de nombre cyclique. Voici ci-dessus par exemple les les nombres entiers naturels 0, 1, 2, 3, 4, représentés en tant que cycles. Un nombre cyclique (ou simplement cycle) est défini par une égalité de la forme : 0 = N, ou cycle N, où N est le nombre au sens tradictionnel du terme. Par exemple, le nombre 7 en tant que cycle s'écrira : 0 = 7, ou cycle 7. Et les égalités comme 1 = 8, 12 = 19, -4 = 3, désignent le même cycle 7. Le cycle N est aussi appelé alternation N ou modèle N, et dans ce cas, il sécrira : (A1, A2, A3, ...., AN), où A1, A2, A3, ..., AN sont des variables désignant N choses distinctes. Par exemple, le cycle 2 sera appelé aussi une alternation 2 (ou alternation bivalente ou alternation binaire), et aussi un modèle 2, et alors on le notera (A, B). Cette écriture veut dire qu'on se donne deux choses absolument quelconques A et B, qui permettent d'énoncer les propriétés générales de cette alternation ou cycle ou modèle.

Voici ci-dessous illustré le cas du cycle 4 ou modèle (A, B, C, D), qui montre aussi la synonymie entre la notion de cycle et la très importante notion de fractale :

Figure 5 : quelques éléments de vocabulaire de l'alternation: cycle, modèle, fractale, symétrie, etc.
ici par exemple, ce qu'on appelle le cycle 4, est un cercle avec quatre points,
qui sont à leur tour des cercles avec quatre points, et ainsi de suite.
Ces quatre points sont les cycles précédents, donc 0, 1, 2, 3, encore appelés A, B, C, D,
et chacun d'eux est fait de la même façon.
Par exemple le cycle 3 est un cercle avec trois points (0, 1, 2) ou (A, B, C),
eux-mêmes des cercles avec trois points, et ainsi de suite.
Ainsi se structurent les nombres avec l'alternation, une structure fractale,
chacun étant une fractale faite des fractales d'avant, et qui sera un élément de la fractale suivante.
La dernière des fractales, la fractale infinie, est la fractale de tous les nombres, appelée simplement le Cycle.
Cette dernière Fractale ou Cycle, c'est tout simplement l'Univers.
Une fractale (ou cycle) est aussi appelée un modèle ou une symétrie, ici par exemple le modèle (A, B, C, D).

Quelle que soit la notion dont on peut parler actuellement (ensemble, fractale, modèle, symétrie, cycle, nombre, équivalence, etc.), elle reste extrêmement faible comparée à sa version de l'alternation. En effet, c'est avec l'alternation que beaucoup (pour ne pas dire simplement toutes) les notions scientifiques acquièrent à la fois tout leur sens et toute leur puissance. Actuellement par exemple, on parle évidemment de cycle, mais on sépare les phénomènes cycliques (ou périodiques) de ceux qui ne sont pas cycliques. Mais avec l'alternation la question est beaucoup simple et puissante, car elle dit simplement que "toute chose est un cycle", tout est cyclique. Ce qui va distinguer une chose d'une autre est le type de cycle qu'elle est : 0, 1, 2, 3, 4, etc., ou infini. Et une même chose, vue sous tel angle ou dans tel contexte sera un cycle X, et vue sous tel autre angle ou dans tel autre contexte sera un cycle Y.

Par exemple, si l'on considère l'heure, elle est un cycle de 60 minutes, un cycle 60, qui s'écrit alors 0 = 60; l'angle sous lequel on voit l'heure est celui de l'unité minute. L'écrirute 0 = 60 traduit la réalité selon laquelle quand l'aiguille des minutes en partant de la position 0 a pourcouru 60 unités, elle revient à 0. Mais la même heure peut être vue sous l'angle de l'unité seconde, et alors elle est un cycle 3600, car elle compte 3600 secondes, et ce cycle s'écrit : 0 = 3600. Et à la question : "Quel cycle exactement est l'heure ?", la réponse est : "Cela dépend du point de vue sous lequel on voit l'heure". Mais la meilleure réponse, qui est celle du type des propos de l'alternation, est : "L'heure est tout cycle". Cela veut dire la même chose, mais l'alternation préfère de loin les réponses positives aux réponses négatives ! En disant seulement : "Cela dépend..." (ici une réponse relativiste...) on ne donne aucune solution particulière. Cette réponse négative (ou relativiste) doit s'accompagner d'une réponse positive (ou absolutiste), une réponse universaliste (ce qui caractérise l'alternation), qui consiste à employer le quantificateur universel, c'est-à-dire le mot "TOUT", comme Univers ! C'est ce qu'on fait en disant : "L'heure est tout cycle". Et à celui qui pose la question de choisir (la notion de choix est aussi extrêmement importante avec l'alternation) dans cette universalité ou infinité de possibilits celle qu'il veut, celle qui lui convient le mieux.

Nous avons pris l'exemple de l'heure pour illustrer que "L'heure est tout cycle". Mais nous pourrions démontrer de la même manière avec toute chose, que "Toute chose est un cycle". Cela fait alors de la notion de cycle quelque chose d'universel, bien plus puissant que la notion actuelle de cycle, qui elle ne concerne que certaines choses et pas d'autres. Avec la négation, on sépare ainsi les choses en celle qui sont "Ceci" et celles qui ne sont pas "Ceci", ou qui sont "non-Ceci". C'est l'un des innombrables problèmes de la négation, qui font d'elle une notion mauvaise et dangereuse. Mais avec l'alternation, "Toute chose est Ceci", le reste étant une simple affaire de contexte. Il y a des contextes où c'est très évident qu'une chose A donnée est Ceci, et des contextes où c'est très peu évident (ou même pas du tout). La phrase "A est Ceci" n'est pas une affaire de Vrai ou Faux, ainsi que l'on raisonne actuellement avec la négation, qui doit trancher entre "A est Ceci" et "A est non-Ceci". Mais avec l'alternation, le degré de vérité de la phrase "A est Ceci" est graduée, et les instruments de graduation sont justement les cycles. La vérité est graduée de 0 (le moins vrai) à N (le plus vrai), si on se trouve par exemple dans le cycle N; sinon le cycle par défaut est le cycle infini, et le maximum de vérité est l'infini.

Prenons l'exemple des cycles eux-mêmes pour illustrer cette importante notion de graduation de la vérité, fondamentale elle aussi dans la logique de l'alternation. Pour simplifier les choses, le A sera ici 0, et le Ceci sera à chaque fois un autre nombre X donné. La phrase "A est Ceci" sera donc une phrase du genre "0 est X".

Par exemple, dans le cycle 60, la vérité va être graduée de 0 à 60. Prenons pour X le nombre 4; dans ce cycle, la phrase "0 est 4" (sa valeur de vérité sera 4 en absolu et 4/60 ou 1/15 en relatif) sera moins vraie que la phrase "0 est 30" (qui a une valeur de vérité 30 en absolue et 30/60 ou 1/2 en relatif), elle-même moins vraie que la phrase "0 est 59" (qui vaut 59 en absolu et 59/60 en relatif); et la plus vraie de toutes sera "0 = 60", le maximum dans ce cycle, 60 en absolu, et 60/60 = 1 en relatif. Mais cette dernière phrase, vaudra en absolu toujours 60 dans le cycle 3600, mais dans ce cycle ne vaudra plus que 60/3600 = 1/60 en relatif. Et maintenant si on se place dans le cycle 0, seule la phrase 0 = 0 est vraie, toute égalité "0 = X" où X n'est pas 0 est fausse. La négation actuelle correspond en fait à ce cycle, toutes les vérités actuellement formulées en science se réduisent à ce seul cycle, auquel correspond une logique qu'on peut qualifier de logique de "Tout ou Rien", la logique actuelle. Pour elle, la phrase "0 est 4" ou "0 = 4" est tout simplement fausse, sans modération aucune de cette fausseté.

Mais avec l'alternation et le cycle, la phrase "0 = 4" (et plus généralement toute phrase) est toujours vraie; le reste est une simple affaire de contexte, ici de cycle. Dans tel cycle (ici le cycle 0) elle est complètement fausse (sa valeur relative est 0 ou 0%); dans tel autre (ici le cycle 4) elle est la vérité maximale (1 ou 100%). La notion de nombre dans le concept de l'alternation est celle de cycle. C'est le nombre (le cycle) qui va tout quantifier, et en particulier la vérité. La notion de vérité n'est pas seulement une affaire Vrai ou Faux, de "Tout ou Rien", c'est à dire (en terme de nombre) seulement une affaire des deux nombres 1 (pour Vrai) et 0 (pour Faux). Ce ne sont pas les seuls nombres qui existent, donc les seules valeurs de vérité possibles. La vérité est graduée en absolu entre 0 et l'infini, et en relatif entre 0 (0%) et 1 (100%). La valeur intermédiaire 50% ou 0.5 existe aussi !

Dans le paradigme scientifique actuel (celui du principe de non-contradiction*), la notion d'égalité est comme celle de négation, elle est tranchée ! Soit la phrase "X = Y" (ou "A est Ceci") est vraie, soit elle est fausse, il n'y a pas d'intermédiaire possible. Mais avec l'alternation la question est infiniment plus nuancée et graduée, ce qui ne veut pas dire que la réponse est floue ou ambigüe ! Bien au contraire, c'est la conception actuelle du "Tout ou Rien" qui est grossière, qui manque cruellement de précision ! Si la justice fonctionnait ainsi par exemple, il n'y aurait que deux jugements possibles : SOIT on est innocent et relâché, SOIT on est condamné à mort, sans circonstance atténuante et sans jugement intermédiaire possible ! Il est très important de trancher par Oui ou par Non, sinon on ne prendrait aucune décision. Or la notion de choix est de décision est extrêmement importante aussi dans l'alternation. Mais la différence avec l'alternation, c'est qu'on tranche APRES avoir finement analysé la situation, car ce paradigme est d'une finesse inouïe ! Là où il n'y avait que deux valeurs (Vrai ou Faux, ou encore 0 ou 1) pour apprécier une vérité, on a maintenant une infinité; il y a donc le choix ! On peut donc ainsi bien comparer les possibilités les unes par rapport aux autres, et prendre forcément la meilleure décision pour la situation en question. On peut ainsi techniquement ajuster avec grande précision les paramètres et faire des réglages extrêmement fins. Et rien n'empêche de renoncer si l'on veut à cette finesse et de revenir au cas grossier et tranché avec une règle du genre : "En dessous de la valeur r valeur c'est Non, et à partir de la valeur r c'est Oui".

A la différence du paradigme actuel, nous avons le choix avec l'alternation, nous avons un libre-arbitre accru, une liberté inouïe, un grand pouvoir de décision; la vérité ne s'impose plus forcément à nous, car c'est nous qui faisons la vérité. On ne fait plus par exemple une physique comme actuellement où l'on se demande si telle théorie est vraie ou non, si ceci ou cela est vérifié ou non dans la réalité, ou si le Boson de Higgs existe ou non. L'alternation fait comprendre que tout est vrai, tout existe dans l'Univers. Le reste est simplement de se mettre dans le bon contexte, dans les bonnes conditions, d'avoir les bons ingrédients, de se donner les bonnes valeurs, de faire les bons réglages, etc., pour que la vérité soit constatée, pour que la chose cherchée soit trouvée, pour que son existence se manifeste ! Et si elle ne se manifeste pas, c'est tout simplement parce qu'on ne s'est pas vraiment mis dans les bonnes conditions, ou qu'il y a des paramètres cachés qui ont fait que nous ne nous trouvions pas dans le contexte où l'on croyait être. Cela va de l'"erreur de calcul" (le fait à un moment donné d'avoir pris un cycle au lieu d'un autre), jusqu'à un déni ou "sabotage" fait par une autre conscience dont nous ignorions l'existence et qui intervenait dans ce que nous faisions, en passant par toutes sortes d'autres causes possibles. Mais en aucun cas il ne faut conclure que la chose n'est pas vraie ou qu'elle n'existe pas dans l'absolu. La fausseté ou la non-existence est toujours relative à un contexte donné, à des conditions données. Sinon, "Toute chose existe", dit le Théorème de l'Existence.

Avec l'alternation, on découvre donc les choses qui de toutes façons existent déjà. Mais aussi on crée ces choses par tout ce que nous mettons en oeuvre pour que leur existence se manifeste. Si par exemple on trouve le Boson de Higgs, on l'aura découvert, mais aussi on l'aura créé, depuis la théorie le décrivant et disant comment il doit être, jusqu'aux expréiences mises en oeuvre pour le détecter. Sinon, on aura simplement raté ce coup-ci sa découverte et aussi sa création, pour X ou Y raisons. Ce sera simplement partie remise, on réussira peut-être la prochaine fois, un jour sûrement. Et si ce n'est pas dans ce monde ou dans cette vie, ce sera dans un autre monde ou dans une autre vie. L'alternation, c'est aussi cela, c'est faire comprendre que d'autres mondes ou d'autres vies existent, des meilleurs, mais aussi des pires... A nous de choisir dès maintenant vers lesquels nous voulons aller, exactement comme à le carréfour en T ci-dessous il faut décider si au point D (le point de décision) on va aller à droite ou à gauche, suivre maintenant le chemin vert ou continuer sur la voie rouge :

Figure 6 : Une chose et son contraire existent toujours toutes les deux dans l'Univers;
à nous à chaque point de décision D de faire notre choix;
la question qui est présentement posée est de savoir
si on veut enfin entrer dans l'alternation, ou au contraire poursuivre dans la négation.
Dans le premier cas, on entre dans des cycles d'existence où c'est nous qui décidons toujours ce qui doit être vrai;
existera sans faute ce que nous souhaitons voir exister, et l'Univers sera tel que nous voulons le créer.
Mais dans le second cas nous n'aurons pas toujours le choix, et nous subirons beaucoup de choses
sans pouvoir les changer, jusqu'au prochain point D de décsion,
où la question sera une nouvelle fois posée de savoir si on veut maintenant le paradis
ou bien si on n'a pas encore assez joui de l'enfer ou des cycles infernaux...

Paradigme du Modèle, paradigme de la Fractale (ou Arbre)

Le cas particulier de la graduation de la vérité de la phrase "0 = X" (et plus généralement "X = Y") ou X et Y sont les nombres (ou cycles), est capital. Ce cas réglé, tous les autres se ramènent à celui-là, en raison d'une autre très importante notion de l'alternation, celle de Modèle, et aussi de Symétrie, d'autres simples mots pour dire Cycle, lui-même un simple autre mot pour dire Alternation. Mais pourquoi différents mots et pas un seul ? Justement à cause de la nature même de l'alternation, avec laquelle on ne voit plus les choses et on ne raisonne plus comme actuellement. La définition même de l'Univers est l'Ensemble de toutes les choses, donc le TOUT. Donc (comme je le redirai plus loin) toute chose, toute notion, tout ce qu'on peut dire (tout et son contraire !), est un aspect du seul et même Univers. Les choses sont différentes, mais on parle finalement de la même Chose, l'Univers; on n'étudie finalement que l'Univers. On parle de la même Chose, mais il faut distinguer les différents aspects de cette Chose, mais en gardant constamment présent à l'esprit le lien entre les différents aspects. Les différentes notions (cycle, modèle, fractale, etc.) expliquent et précisent un peu plus ce qu'est l'alternation, et toutes précisent un peu plus ce qu'est l'Univers.

Ce que j'ai appelé par exemple le cycle 2 en tant que nombre (donc comme une chose globale dans entrer dans les détails de ses éléments 0, 1), c'est ce que je vais appeler modèle (0, 1), et cette-fois en m'intéressant à 0 et 1 en tant que deux choses différentes, et non plus forcément des nombres ou cycles. Par 0 et 1 il faut entendre maintenant "première chose du cycle 2" et "seconde chose du cycle 2", et alors je les appelle modèle (A, B). Quand il s'agira de découvrir les propriétés logiques des mêmes choses 0 et 1 ou A et B, je les appellerai Vrai et Faux, mais au sens de l'alternation et pas de la négation. En effet, 0 et 1 sont aussi vrais l'un que l'autre, ils jouent dans l'alternation un rôle parfaitement symétrique, d'où la notion de symétrie elle aussi très liée à l'alternation et au cycle.

Comme la notion de cycle, celle de modèle est extrêmement puissante avec la notion d'alternation. De même qu'actuellement une chose A n'est pas forcément un cycle, de même un modèle donné ne s'applique qu'à certaines choses et pas à d'autres. Mais avec l'alternation, la notion de modèle est totale, comme celle de cycle. Cela veut dire que dès qu'on a établie les vérités pour un modèle donné est valable pour tout ce qui possède la forme de ce modèle. C'est important de noter qu'on ne s'intéresse qu'à la FORME d'un modèle et non pas à son sens, c'est-à-dire à toute interprétation qu'on peut faire des choses intervenant dans le modèle. C'est ainsi par exemple que, comme déjà dit, le cycle 2 ou nombre 2 en tant que modèle signifie simplement "Deux choses" ou (A, B). Cela veut dire alors que toutes les vérités que je vais établir pour ces deux choses en tant qu'éléments du modèle, concerne la forme du modèle, à savoir "Deux choses", et non pas au sens de ces deux choses. Peu importe donc si on les appelle 0 et 1, A et B, l'Une et l'Autre, Prémière et Deuxième, Chat et Chien, Adam et Eve, Dieu et Diable, etc. Avec le cycle 2 en tant que modèle, on fait comme si on ne sait pas ce que peuvent signifier ces mots. Et justement on ne le sait pas, car tout sens qu'on pourrait leur donner est subjetctif. Pour commencer à savoir ce qu'ils signifient, il faut justement faire parler le modèle. Et tout ce qu'il dira sera alors valable pour tout couple de choses, y compris Dieu et Diable ! Et c'est précisément ainsi que l'on va commencer à savoir ce qu'il faut entrendre par Dieu ou par Diable, du fait que tout ce qui est vrai pour A et B est vrai pour eux aussi.

Le modèle est le moyen le plus rigoureux de définir les choses et de savoir ce qu'elles sont ! Sans cela, toute affirmation les concernant relève de la pure sujectivité. De même qu'on ne doit avoir aucun préjugé quant au sens des choses dans le modèle (avant de savoir ce que dit le moèle), de même on ne doit pas non plus avoir de préjugé sur ce à quoi il faut appliquer ou non le modèle. Le modèle a parlé un point c'est tout, et sa parole est universelle, absolue, souveraine, et s'applique sans distinction ou ségrégation ou a priori ou préjugé, à toute chose qui a la FORME du modèle !

Et en particulier donc, tout ce que je peux dire du cycle 1 ou modèle (A), donc tout ce est vérifié par le modèle fait d'une seule chose, est valable pour toute chose ! Le cycle 1 ou modèle (A) est donc le modèle universel par excellence, que j'appelle aussi le modèle unaire. On peut croire qu'il est "pauvre" car il se réduit à une seule chose. Il est SIMPLE mais pas pauvre ! Sa simplicité fait aussi toute sa puissance. Son étude est d'une profondeur inouïe, car c'est lui qui révèle les secrets les plus cachés et les plus étonnants de l'Univers, des choses qu'on ne pouvait nullement soupçonner jusqu'à présent.

Le cycle 1 n'est fait que d'une seule chose, le 0. Autrement dit, le modèle (A) n'est fait que d'une seule chose, appelée A. Et avec une seule chose A, on a qu'une seule opération simple et bête qu'on peut faire : la répétition de la chose. Si par exemple on une langue n'a dans son alphabet qu'une seule lettre A, alors les mots de cette langue sont : A, AA, AAA, AAAA, etc. De la même façon, si un peuple, pour écrire les nombres, n'avait qu'un seul chiffre, noté 0 par exemple, il écrirait : 0, 00, 000, 0000, etc. N'oublions pas que ne devons donner aucun sens a priori au 0, car ce n'est pas du 0 signifiant "rien" que nous parlons ici, mais seulement d'un symbole pour dire "une seule chose". C'est le sens à lui donner, il décrit seulement la FORME du modèle. Ainsi, donc il revient exactement au même si ce symbole est 1 seul, 7 seul, ou tout autre symbole. Si c'est pour traduire des quantités, cela revient tracer un trait "I" pour dire "un", deux traits "II" pour dire "deux", trois traits "III" pour dire "trois", etc. C'est d'ailleurs ainsi que commence la numération romaine ! On la qualifierait assurément de "rudimentaire" ou de "primitive" si on continuait ainsi, et c'est justement ce qu'est le modèle unaire, que j'appelle aussi le système de numération unaire.

Très simple en effet. Sa seule opération donc : la répétition de la même chose ! Répétition comme cycle, car une chose cyclique est justement une chose qui se répète indéfiniment ! Et répétition comme... fractale, car on appelle une fractale le fait qu'un même modèle se répète identiquement à lui-même indéfiniment ! Le modèle en question ici est "une seule chose", noté (A). On ne se préoccupe pas de savoir ce qu'est A, mais seulement du fait qu'il se répète indéfiniment ! C'est donc la propriété fondamentale de ce modèle (A), il est la simple définition de la fractale,

 

Figure 7 : La logique alternative est une logique fractale

Une fractale est un modèle (notion extrêmement importante associée au concept d'alternation), qui se répète identiquement à lui-même infiniment. Derrière le mot "répétition" se cache évidemment la notion de cycle vue plus haut. C'est avec l'alternation que la notion de strucure fractale prend tout son sens, et en relation très intime avec la structure des ensembles, qui est une structure fractale (ou arborescente), mais aussi la nouvelle logique, la Logique alternative (ou logique de l'alternation), qui est aussi une logique fractale (ou arborescente). C'est la structure même de l'Univers, son fonctionnement le plus profond, qui est décrite par cette strucure fractale. Et à tout cela est associée une très puissante notion de symétrie, ou de "rôles symétriques", elle-même qui engrendre une toute nouvelle et puissante notion d'égalité, que l'on qualiferait actuellement par la notion d'équivalence.--

Comme le courant alternatif

La notion d'alternation assimiliée, le reste coule de source, tout devint très clair, tout devient tout à coup très logique (et plus particulièrement ce qui paraissait "contradictoire" ou était appelé "contradiction"). Avec l'alternation, on comprend vraiment les choses, tout s'explique, tout devient logique...

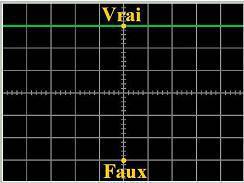
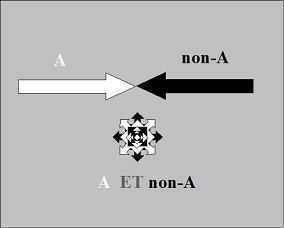
Logique continue et Logique alternative

Une manière simple rapide d'entrer dans le concept d'alternation, est de voir ce concept comme le courant alternatif (image de droite ci-dessus), par opposition au courant continu (image de gauche). Une autre manière est d'imaginer deux enfants A et B jouant à la balançoire (situation alternative ou "modèle à deux" de l'alternation) par opposition à un enfant A seul sur une des deux extrémités de la balançoire (situation continue ou "modèle à un" de l'alternation), attendant que son copain B arrive pour s'asseoir sur l'autre bout, pour que le "jeu" (l'alternation proprepent dite) commence. Le jeu de la "chaise musicale", où il y aurait autant de chaises que de joueurs, est un exemple d'alternation à plusieurs. S'il y a par exemple 25 joueurs, on peut imaginer les chaises marquées de 0 à 24. Le numéro de la chaise sur laquelle on réussit à s'asseoir quand la musique s'arrête donne autant de points pour la manche. Pour que le jeu soit vraiment une alternation au plein sens du terme, il faut qu'il se poursuive indéfiniment ou qu'il y ait un très grand nombre de manches, pour donner à chaque participant l'occasion d'avoir le même nombre de points au final.

Dans le monde de l'alternation, on peut perdre à une manche, il y a toujours des différences à chaque étape, mais au final tout le monde gagne, tout le monde est égal. L'égalité entre les choses dont on parle dans ce monde, n'est pas obligatoirement l'égalité contextuelle ou ponctuelle (bien que celle-ci ne soit pas exclue non plus), car il peut y avoir des différences contextuelles ou ponctuelles (et d'ailleurs il faut justement ces différences pour la diversité des choses et pour que l'alternation soit intéressante et même ait simplement un sens); mais on parle d'égalité générale, d'égalité d'ensemble, d'égalité universelle, d'égalité finale, etc., car au final toutes les choses sont égales. La différence est très importante seulement pour assurer la diversité des choses. En gros, "on n'est pas les mêmes à chaque fois, car il faut qu'on soit différent, pour jouer des rôles différents; mais finalement on est les mêmes, car il faut aussi qu'on soit égaux, car les rôles tournent ("permutent", "alternent"), et à la fin chacun aura joué tous les rôles".

On comprend par exemple qu'on puisse militer pour l'égalité entre riches et pauvres, et plus généralement encore militer pour l'égalité entre tous et à tous les niveaux. Il y a deux façons de résoudre ce problème : La première est que tout ait le même salaire, la même maison, la même voiture, etc. Bref, dans tout contexte et sur tout point il faut qu'il y ait une égalité. Cette solution est semblable au courant continu représenté ci-dessus. Et la seconde manière de résoudre le problème fait appel à l'égalité (non plus "continue") mais alternative. Elle consiste à maintenir toutes les différences, même les plus gigantesques et "injustes", mais à imposer l'alternation dans la société. Par exemple, un coup c'est A qui est riche et B qui est pauvre, et une autre fois c'est l'inverse. Si le premier habite un palais et le second un taudis, on décide d'un moment où le premier va connaître la vie de taudis, tandis que le second va connaître la vie de palais. Et plus généralement, la société tourne sur chaque rôle ou situation, on permute continuellement sur les places, chacun joue alternativement tous les rôles, les meilleurs comme les pires, les plus valorisants comme les plus dévalorisants. Du fait de l'alternation, tout le monde est finalement à la même enseigne, les mêmes avantages et les mêmes inconvénients. Ponctuellement, à chaque instant et contextuellement, tout le monde est différent, il y a de grandes inégalités, parce qu'il faut ces différences. Mais globalement, universellement, tout le monde est égal. J'espère que ces quelques exemples suffisent à se faire une bonne idée de la sa philosophie.

Contextualité (Relativité) et Universalité (Absoluité)

L'alternation est une notion très simple, très intuitive, et extraordinairement puissante. Lui sont associées les notions actuelles de permutation, de contextualité, d'universalité, de choix, et d'autres ! C'est avec l'alternation que ces notions prennent en fait leur vrai sens et sont les plus puissantes.

La notion de permuation est fondamentale dans l'alternation. Un verbe important dans la Science Nouvelle, qui est associé à l'alternation, est le verbe alterner, qui signifie donc : "Passer de l'un à l'autre, et vice-versa". Et au sens le plus général, alterner est simplement synonyme de permuter. C'est donc "changer les rôles", ou "intervertir les rôles", ou "redistribuer les rôles", etc

Nous utilisons l'alternation, très instinctivement sans nous en rendre, et c'est sans doute parmi les notions dont nous avons le moins conscience, tellement justement elle est naturelle. Comme toutes les choses naturelles et très fondamentale, cela paraît tout à coup difficile quand on les met en évidence et on en fait une théorie, surtout quand cette théorie est mathématique. Par exemple, nous avons une conception instinctive, très intuitive et naturelle de la notion de nombre, et même des opérations élémentaire avec les nombres (addition, soustraction, etc.). Mais dès que ces notions deviennent une science qu'il faut étudier comme par exemple les maths, les choses se gâtent. Et j'espère que les choses ne vont pas se gâter maintenant que je mets en évidence cette chose très naturelle d'alternation et que je fais prendre conscience de l'usage que nous en faions très couramment.

Voici un simple exemple en mathématique élémentaire : le fait de tracer une droite, de choisir un sens qui sera le sens positif, puis de choisir un point sur la droite pour en faire l'origine ou le 0, puis de choisir une longueur qui servira d'unité de graduation de la droite et donc indiquer le point 1 :

Maintenant que j'ai par des exemples donné une description de l'alternation, voit-on dans cette simple activité (qui consiste à se donner ce qu'on appelle un axe gradué ou un répère) une application de l'alternation ? Ou plus simplement, voit-on ou se cache l'alternation dans ce qu'on vient de faire ? Si oui, alors on va aussi commencer à découvrir de surprenantes et très simples vérités. Si on les ignorait jusqu'ici, c'est parce qu'on ignorait aussi l'existence de l'alternation, on n'avait pas conscience que beaucoup de choses qu'on faisait reposent sur elle, et que sans elle on ne pourrait pas le faire.

L'un des aspect très banal de l'alternation qui nous a permis de faire cette activité est celle de choix et de décision. Nous avons fait des choix et pris des décisions tout au long du processus. Mais nous savons aussi que nous aurions pu faire d'autres choix, qui respectent les mêmes consignes, et qui atteignent le .même but. Mais le problème est qu'une fois un choix fait, nous "oublions" les autres possibilités, et faisons comme s'il n'existe que celle que nous avons choisie. En dautres termes, nous ne concevons pas toutes les possibilités comme simulténément vraies. Si nous faisions, nous aboutirions très vite à des vérités aussi simples que puissantes, mais que nous considérons comme des contradictions.

Par exemple, nous aurions pu aussi faire le choix ci-dessous, indiqué en rouge sous le précédent :

Les deux mis ensemble, cela nous dit simplement que ce que nous avons appelé le 0 dans un choix donné, aurait tout à fait pu être le 1 dans un autre choix, le -20 dans un autre encore, le 4563 dans autre encore, etc. Et du mot autre en mot autre, nous comprenons que le 0 d'un certain point de vue, est aussi le 1 d'une autre point de vue, le -20 d'un autre encore, le 4563 d'un autre encore, etc. Bref, tout nombre est potentiellement tout autre nombre. Toutes les possibilités et toutes les combianisons (ou permutations ou alternations) existent. Mais à un moment donné, dans un contexte donné, nous faisons le choix d'une possibilité, et les autres sont alors masquées, comme si elles n'existent pas, alors qu'elles existent ! Il est important de voir les choses ponctuellement ou dans un certain contexte. Mais il est tout aussi important de voir les choses dans leur globalité, dans leur universalité, et alors d'autres vérités (les vérités universelles) apparaissent. Ici par exemple, nous dévrons simplement que 0 = 1 ! Ce genre de propos semblent absurdes ou contradictoires (contraires à la logique), ou ils semblent être en contradiction avec les vérités contextuelles ou ponctuelles. Mais les deux vérités se complètent, et plus exactement, les vérités universelles englobent les contextuelles.

Autre exemple voisin, très banal, dans la pratique courante des mathématiques. Le mathématicien utilise beaucoup une notion nommée variable, mais sans réaliser que notion doit sa puissance à l'alternation. Avec la variable X par exemple, il dira tantôt X = 0,une autre fois X = 1, une autre fois X =-20, une autre fois X = 4563, etc. Et du mot autre en mot autre, par le pouvoir de l'alternation, X peut être tout ce qu'on veut, il est potentiellement tout nombre. Là encore, à moment donné, dans un contexte donné, nous faisons le choix d'une valeur pour X. Et bizarrement nous oublions les autres contextes, et faisons comme si seul le contexte courant existe. Mais les autres existent aussi, toutes les permutations existent. Si nous avions auparavant fait X = 0, ce n'est pas parce que nous faisons maintenant X = 1 qu'il faut oublier X = 0. En prenant globalement en compte tous les contextes comme le fait de considérer simultanément tous les "univers parallèles", il apparaît simplement que la seule et même chose nommée X est à la fois 0, et à la fois 1 ! Si une même chose est égale à deux autres, alors ces deux autres sont égales entre elles. C'est une loi élémentaire de l'égalité appelée la transitivité. Puisque nous disons X = 0, X = 1, il appraît cette vérité, 0 = 1, que nous concevons comme contradictoire, mais qui pourtant n'est qu'une vérité globale, une vérité universelle.

L'Univers fonctionne suivant l'alternation, et c'est ce que je veux démontrer plus amplement dans toute la suite. Quand j'écris par exemple 0 = 1, il s'agit d'une égalité au sens de l'alternation : "0 et 1 sont contextuellement deux choses différentes, mais universellement sont la même chose." Dans une logique qui n'est pas alternative, cette égalité est une contradiction ou une impossibilité. Or elle est bel et bien une vérité, dans une autre conception de l'égalité, celle de alternation.

Vidéo : Noir et Blanc : l'Universalité !

Pour aller plus loin...

L'Affirmation et la Négation, en toute rigueur

Les connecteurs Oui et Non

Les propriétés essentielles de l'alternation 2 sont données par les tableaux suivants, qui sont deux opérateurs Op1 (appelé Oui) et Op2 (appelé Non), que cette alternation permet de définir. Ce sont simplement les deux permutations du couple (A, B), qui sont (A, B) et (B, A). :

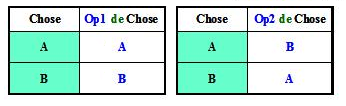
Les deux tables de l'alternation 2, la table du connecteur Oui et du conncteur Non.

Voici les propriétés des deux opérateurs :

Oui A = A
Oui B = B
Non A = B
Non B = A

L'alternation et la notion de signe

Le couple qui en logique s'appelle (Oui, Non), est tout simplement le même que celui qui s'appelle (Positif, Négatif) ou (Plus, Moins) ou (+, -) dans le contexte des nombres, comme nous allons le prouver maintenant grâce aux propriétés caractéristiques qui établissent leur identité, qui nous permettent de dire qu'on parle fondamentalement de la même chose, à savoir la "règle des signes" qui leur est commune qui est la suivante :

Règle des signes commune aux couple (Oui, Non) et (+, -)

On est habitué à la classique règle des signes en algèbre et à son fonctionnement, mais peut-être pas à la version logique de cette règle. Et pourtant dans le vie courante, le citoyen lambda dans ses raisonnements l'utilise très souvent sans en être conscient sans doute. Quelques explications suffisent à montrer qu'elle est très familière :

Affirmer (ou confirmer) une affirmation, c'est affirmer; mathématiquement : Oui (Oui A) = Oui A = A ou simplement : Oui Oui = Oui;
Affirmer (ou confirmer) une négation, c'est nier; mathématiquement : Oui (Non A) = Non A ou simplement : Oui Non = Non;
Nier une affirmation, c'est nier; mathématiquement : Non (Oui A) = Non A ou simplement : Non Oui = Non;
Nier une négation, c'est affirmer; mathématiquement : Non (Non A) = Oui A = A ou simplement : Non Non = Oui.
Quelque chose me dit que ces règles plairaient beaucoup à "Oui-Oui" du pays des jouets...

Ceci a donc pour but de prouver d'abord l'existence d'un connecteur d'Affirmation associé au connecteur de Négation; ensuite que la notion numérique de "signe", (+, -) n'est autre qu'une notion logique de "signe". Autrement dit, le connecteur de négation Non et la notion de "signe négatif" (comme par exemple dans "-1" ou "-5") sont la seule et même chose. Par conséquent, les signes des particules (le signe de leur charge électrique), comme par exemple le proton (+) et l'antiproton (-) est fondamentalement une affaire de logique, de (Oui, Non) ou de (Vrai, Faux). Et donc le photon qui a un signe nul (sa charge électrique est 0), correspond à une troisième valeur de vérité, entre Oui et Non, ou entre Vrai et Faux, donc du genre "Oui ET Non" ou "Vrai ET Faux" (on en reparlera plus loin au sous-titre La troisième valeur de vérité et la physique).

L'alternation et la théorématique

Mais il est très important de signaler que la négation Non et le signe (-) ou (-1) sont la même chose, uniquement quand on se place dans un "modèle à deux" ou modèle binaire. Par exemple, le couple (proton, antiproton) forme un modèle binaire, et dans ce modèle seulement, il revient au même de dire Non proton (ou non-proton) que de dire antiproton ou (-proton), c'est-à-dire donc le proton dont on inverse le signe. De même, dans le modèle binaire (proton, antiproton), dire Non antiproton c'est dire (-antiproton) ou (-(-proton)), donc proton.

Mais d'une manière générale (donc quand on ne se limite plus à un modèle binaire), un Non proton n'est pas nécessairement un antiproton, l'antiproton ne constituant qu'un cas très particulier de choses répondant au signalement non-proton, comme par exemple aussi l'électron, le neutron, le graviton, etc., et aussi le caillou, l'humain, le soleil, la lune, etc.

Plus généralement, dans un modèle binaire (A, B), on a : Non A = B, et Non B = A, et donc aussi Non A = -A, et Non B = -B; autrement dit, on assimile le connecteur de négation Non au signe négatif (-) ou (-1). Mais dans un "modèle à trois" (A, B, C), Non A c'est B ou C; et Non B c'est A ou C; et Non C c'est A ou B. Et pour être plus précis encore, un "modèle à trois" (A, B, C) est défini comme un "modèle à deux " (A, B'), où la chose B' est un "modèle à deux" (B, C). Et un "modèle à quatre" (A, B, C, D) est défini comme un "modèle à deux " (A, B'), où la chose B' est un "modèle à trois" (B, C, D); qui lui-même est donc un modèle "à deux" (B, C'), où la chose C' est un "modèle à deux" (C, D). Et on définit de la même manière un "modèle à cinq", un "modèle à six", etc. Dans la Science Nouvelle, il suffit d'être capable de définir ainsi un "modèle à n" quelconque, quel que soit le nombre n dont on parle, pour qu'on ait défini aussi le "modèle à une infinité de choses", quelle que soit la taille de l'infini dont on parle, car on démontre dans la Science Nouvelle que tous les infinis se ramènent finalement à un seul infini, appelé Oméga, qui lui-même n'est que l'autre façon de dire Zéro ou 0 (voir la vidéo L'Algèbre du Cycle) ! De toutes façons on démontre tout dans cette science..., oui "Tout est vrai", dit-elle, sans que cela ne soit pour autant contradictoire ! C'est d'ailleurs le sujet traité ici, et la négation est justement au coeur de l'affaire...

Tous les modèles peuvent donc se ramener à un "modèle à deux", d'où l'importance particulière accordée à ce modèle, dont les résultats fondamentaux seront les résultats de base des modèles supérieurs, tout comme le "modèle à un" (eh oui il existe aussi ! et il est extrêmement important) lui fournit ses propriétés de base, qui ne sont pas étudiées dans ce document, pour ne pas aller trop loin. De même ne sont pas édudiées ici les propriétés spécifiques des modèles supérieurs à deux, et en particulier du modèle infini (ou modèle Oméga), qui n'est autre que le modèle zéro (ou modèle Alpha), et la boucle est bouclée !

Le "modèle à deux" (A, B) possède 2 alternations ou permutations ou "symétries" (notion très importante); ce qui veut dire qu'il y deux façons équivalentes d'écrire le couple (A, B), à savoir (A, B) et (B, A). Tout ce qu'on a dit pour (A, B) reste valable par symétrie de rôles pour (B, A). Autrement dit, toutes les phrases parlant de A et B restent vraies en remplaçant A par B et B par A, en alternant A et B, comme je le dis. C'est ici que se trouve le secret même du principe d'alternation, quand je l'énonce ainsi : "Le contraire de toute vérité est une autre vérité", ou simplement "Tout est vrai".

Le "modèle à trois" (A, B, C) possède 6 alternations (ou permutations ou "symétries"); car on a 3 façons de choisir parmi les trois (A ou B ou C) qui sera le premier pour faire un "modèle à deux". Puis pour chacune des trois il y a 2 façons de choisir le deuxième, qui sont simplement les 2 façons de faire un "modèle à deux" avec les deux restants; car n'oublions pas qu'on ramène tout à un "modèle à deux". Pour cette raisons, le "modèle à quatre" (A, B, C, D) possède 24 alternations; en effet, il y a 4 façons de choisir le premier pour faire un "modèle à deux", et pour chacune, 6 "modèles à deux" possibles". Et pour un "modèle à n", il y a en tout n! alternations, où n! désigne la factorielle de n ; n! = n x (n-1) x (n-2) x ... x 4 x 3 x 2 x 1. Toutes les vérités établies pour une alternation donnée sont valables pour toutes les alternations, et ce peu importe le sens que l'on donne aux mots A, B, C, D, etc., et même si c'est Vrai, Faux, Dieu, Diable, etc. ! On établit ici des vérités universelles, qui ne doivent souffrir d'aucun a priori philosophique ou autre. Pour autant, on ne vide pas non plus les mots de leur sens naturels au profit d'un sens abstrait, comme le fait actuellement avec l'axiomatique par exemple. La Science Nouvelle est à l'opposé de la science abstraite, et pour elle on peut justement mettre n'importe quel mot derrière les modèles généraux qu'elle établit, comme ici pour A, B, C, D, etc.. C'est justement la bonne manière préciser dans une seule et même opération le sens de tous les mots.

Par exemple, tout ce que je dis pour A est valable pour Dieu, et cela permet ainsi de savoir vraiment ce qu'est Dieu. Chaque vérité, chaque propriété que j'établis nous dit à chaque fois un peu plus sur Dieu. Et c'est valable aussi pour le Diable, puisque je peux prendre pour "modèle à deux" le couple (Dieu, Diable), l'un étant de ce fait le contraire de l'autre et vice-versa. Et il suffit d'inverser (d'alterner comme je dis) ce couple pour avoir le couple (Diable, Dieu), pour inverser toutes les vérités précédemment dites, et pour dire donc les vérités contraires, selon le principe d'alternation : "Le contraire de toute vérité est une autre vérité", ce qui fait que finalement "Tout est vrai". Ce "modèle à deux" permet de dire que Dieu et Diable ne sont que deux faces opposées d'un même être. Et je peux prendre pour couple (Dieu, Homme), et alors ce sont les vérités profondes, toutes les vérites possibles et imaginables, qui concernent Dieu et l'Homme, que je peux ainsi découvrir et exprimer scientifiquement; etc. C'est donc une philosophie et une approche de la vérité radicalement différente de celle de l'axiomatique ou du formalisme traditionnel, et aussi de la philosophie analytique classique (voir aussi La question de Dieu et du Diable aujourd'hui). Cette méthode de la que je suis ainsi en train de faire découvrir est la théorématique. Autrement dit, c'est la science totale, dans laquelle "Tout est vrai", tout énoncé (quel qu'il soit) devient un théorème.

Multiplication des sens, multiplication naturelle

A la découverte du formalisme naturel

Dans la droite ligne du sous-titre précédent sur la notion d'Affirmation et de Négation, et dans la nouvelle conception du sens des mots, revenons sur les opérations que je viens de faire avec les opérateurs Oui et Non pour mettre en évidence une importante notion cachée dans ces opérations : la "multiplication des sens". C'est une notion dont la nature est sans doute très mal connue dans les mathématiques actuelles.

Et plus généralement, j'invite donc à découvrir les bases du formalisme naturel, celui qui conserve le sens naturel ou intuitifs des mots, et s'attache à faire découvrir les règles de base de la formation de nouveaux sens à partir d'autres sens. La recherche de la rigueur mathématique ou scientifique ne doit pas nécessairement signifier l'abandon du sens intuitif des mots. Le nouveau formalisme (celui de la théorématique) s'oppose donc au formalisme artificiel, celui de l'axiomatique, qui lui au contraire vide les mots de leurs sens intuitifs pour un sens purement abstrait.

Pour autant, la nouvelle démarche n'est pas non plus de l'intuitionnisme au sens classique du terme. Car celui-ci reste tributaire du principe de non-contradiction, tandis que le nouvel intuitionnisme que j'introduis s'en affranchit. Voyons les principes de base du formalisme théorématique...

Par exemple, dans la pratique courante des mathématiques, je peux dire que je définis une fonction F, qui à un nombre réel X associe un nombre Y qui est son double. On écrit généralement : Y = 2 x X, qui est une simple addition physique (ou concaténation) de "2", "x" et "X"; et en omettant le signe de multiplication "x", on écrira : Y = 2X, et on lira "Deux X".

Considérons un autre aspect du même exemple. Au lieu de Y = 2X, on écrit souvent aussi : F(X) = 2X, où "F(X)" est à lire "F de X". Or en toute rigueur et simplicité, cette écriture dit simplement qu'à partir d'une chose F et d'une autre chose X, je forme une nouvelle chose, qu'on peut simplement écrire : F X. Et alors cette addition physique de "F" et "X" est la même opération fondamentale que celle que je fais en écrivant "2X" ou "2 x X".

Et maintenant, considérons une deuxième fonction G, qui elle associe à X sont triple. On écrira alors habituellement : G(X) = 3 x X ou G(X) = 3X, qui très fondamentalement peut s'écrire simplement : G X = 3 x X ou G X = 3X.

Et enfin, à un nombre X donné, je peux lui appliquer G pour avoir G(X) ou GX, puis à ce résultat appliquer F pour avoir ce qu'on note habituellement F(G(X)), mais qu'on peut simplement écrire : F G X, pour toutes les raisons expliquées. Toutes les informations pour faire cette opération se trouvent en effet dans F G X, les parenthèses ne servant juste qu'à éviter les éventuelles ambiguïtés.

On parle alors d'avoir effectué une composition des fonctions F et G, opération notée généralement "o" et lue "rond". Autrement dit, ce faisant, j'ai appliquée une nouvelle fonction notée F o G à X pour avoir F G X ou 2 (3 X) = 6 X. La nouvelle fonction F o G, qu'on appellera H, est donc celle qui à X associe X multiplié par 6.

C'est cette opération de composition "rond" ou "o" que j'ai faite entre les opérateurs Oui et Non quand j'écris par exemple : Oui (Non A) = Non A. Cela signifie que je considère d'abord une chose A, à laquelle j'applique l'opérateur Non, pour avoir Non A. Puis à ce résultat j'applique l'opérateur Oui pour avoir : Oui (Non A). Et comme l'opérateur Oui a pour propriété de ne pas changer ce qu'on lui donne mais de le restituer tel quel, le résultat final est donc Non A. J'ai donc ainsi composé Oui et Non, pour avoir un nouvelle opérateur Oui o Non, qui équivaut à Non; c'est-à-dire on a : Oui o Non = Non.

Mais, d'une manière générale, cette composition F o G peut simplement s'écrire : F G, car là encore j'ai toutes les informations pour trouver H, à condition de comprendre que ce que j'appelle n'est que la même opération fondamentale faite depuis le début. Autrement dit, je fais la même simple une addition physique de F et G, pour avoir un nouveau mot F G, que j'appelle H. Ainsi aussi, au lieu de dire Oui o Non (qui signifie une opération entre deux fonctions Oui et Non) j'applique directement Oui à Non (qui signifie que je calcule la fonction Oui pour la chose nommée Non, tout comme j'applique directement 2 à X pour avoir 2X), en écrivant Oui Non, et cela donne Non; c'est-à-dire on a : Oui Non = Non.

Simplicité, économie, concision et précision...

Ainsi donc, j'ai fait une multitude d'opérations conçues différemment en mathématiques actuellement ("2 x X" ou "2X", "F de X", "F o G", etc.), qui toutes se ramènent à une même opération fondamentale, qui consiste "bêtement" à additionner physiquement (à concaténer, à aligner bout à bout) les différentes choses en présence (c'est-à-dire leurs noms, les mots ou les symboles qui les représentent) pour obtenir une nouvelle chose, et plus précisément son nom, son symbole, son expression. Et si on craint une éventuelle ambiguïté un manque de précision concernant l'opération qu'on fait, ce problème se résout très simplement en donnant un nom (ou un symbole) à l'opération qu'on fait, et en faisant figurer explicitement ce nom (ou ce symbole) dans la chaîne (ou addition physique des mots). C'est ce qu'on fait avec "2 x X" (explicitant "2X") pour indiquer qu'on multiplie des nombres; avec "F de X" pour qu'on associe à X par le fonction F; avec "F o G" pour dire que l'on compose deux fonctions, etc. Dans tous les cas, on fait toujours la même opération fondamentale, sauf qu'on ajoute un mot en plus pour faire une "opération à trois", au lieu de faire une "opération à deux". Par exemple, quand j'écris "F de X", je fais simplement cette opération fondamentale avec "F", "de", "X"; et dans "F o G", je la fais avec "F", "o", "X". Le tout est simplement de se demander si ces précisions supplémentaires se justifient vraiment, ou si on n'est pas coupable de redondance (comme cela arrive très fréquemment dans les sciences actuelles), d'un péché de distinguos inutiles (alors qu'on parle en fait d'une seule et même chose sans le savoir), ce qui entraîne une inflation et une complication inutile du discours scientifique.

Mais si la distinction ou la précision se justifie vraiment, il n'empêche que tout cela se ramène toujours finalement à aligner physiquement différents symboles pour obtenir un nouveau symbole désignant une nouvelle chose. Il y correspond une combinaison de différents sens (les sens des différentes notions en présence) pour obtenir un nouveau sens. Cette addition physique pure et bête des mots s'accompagne d'une opération de leurs sens, qui est intuitivement ce que nous appelons une multiplication. C'est ce que je veux simplement mettre en évidence ici. Tout ce qu'on fait revient fondamentalement à cela, et cette opération très basique à laquelle tout se ramène mérite une attention et une étude très particulière, car elle cache de très profonds et grands secrets sur la nature des choses (des objets de l'Univers) dont on n'a certainement pas eu conscience jusqu'ici. Il importe beaucoup de parler en sachant de quoi on parle très exactement. Si par exemple on parle de l'Univers d'une part, dont on ne nie certainement pas l'existence, et de Dieu dont on nie l'existence ou on doute de l'existence, cela suppose que l'on sait ce qu'est vraiment l'Univers, ce qu'il peut être ou ne pas être, et certainement pas Dieu. Et on sait aussi ce qu'est Dieu, ce qu'il peut être ou ne pas être, et certainement pas l'Univers. Sinon, on n'affirmerait pas l'existence de l'un tandis que l'on nie ou que l'on doute de celle de l'autre, si on avait compris qu'on parlait de la même chose avec deux mots différents ! Voilà comment on peut se contredire sans le savoir, tout simplement parce qu'on croit savoir de quoi on parle, que ce soit de l'Univers ou de Dieu.

C'est tout le danger des mots, quand avec eux on peut faire des distinguos inutiles, distinguer très minutieusement Dieu et Univers, porc et cochon, ensemble et collection, égalité et équivalence, multiplication et composition, etc.; quand avec eux on confond gravement des choses là où au contraire il faut soigneusement les distinguer (par exemple négation et négation, contradiction et contradiction...); quand avec eux on peut tourner en rond; quand avec eux on peut parler pour ne pas dire grand chose; quand avec eux on peut débattre avec acharnement et se contredire mutuellement, sans savoir qu'en réalité on parle des mêmes choses; et quand avec eux on peut dire sans le savoir tout le contraire de ce que l'on croit dire, etc.. C'est pourquoi donc en matière de philosophie, je préfère de loin l'approche analytique des choses, qui a le mérite de proposer une arithmétique précise des mots, d'apprendre à combiner avec grande rigueur les sens pour avoir de nouveaux sens. C'est dans cet esprit que s'inscrit l'analyse que je fais ici. Pour une étude spéciale du problème de Dieu impliquant la notion de négation (et donc aussi le problème de la contradiction), voir par exemple le document La question de Dieu et du Diable aujourd'hui.

Les rudiments de l'arithmétique des sens

Ceci dit, revenons à l'opération fondamentale que je viens de mettre en évidence, qui a pour but de faire remarquer que tout le discours scientifique se réduit à l'art d'aligner bêtement des mots ou ses symboles les uns après les autres pour avoir de nouveaux symboles, qui pourront à leur tour être alignés avec d'autres pour former encore de nouveaux, etc. C'est ainsi par exemple que j'aligne les mots pour constituer le présent paragraphe. Et de ce point de vue, l'activité scientifique n'est pas différente de celle de la littérature, de la philosophie, de la religion ou autres ! C'est pure illusion de croire on peut séparer les domaines comme on le fait actuellement, car tous se ramènent à la même activité fondamentale que je suis en train de décrire. On pouvait donc aborder la science par cette activité élémentaire, découvrir ses règles et lois profondes, et établir des vérités universelles en toute simplicité !

Il a suffi par exemple de considérer deux choses ou mots absolument quelconques A et B (ou couple (A, B)) pour définir ce qu'il faut entendre par "négation" et dégager ses propriétés profondes (celle du "modèle à deux"), qu'on est très loin d'épuiser ! Au nombre de ces propriétés il y a d'abord le fait que le couple (A, B) est aussi le couple (Oui, Non), qui obéit à la fameuse règle des signes, sans avoir nullement eu besoin d'entrer dans une algèbre sophistiquée pour la découvrir. Nous découvrons que cette règle est fondamentalement une règle de logique, que tout le monde emploie intuitivement dans son raisonnement de tous les jours : Oui Oui = Oui; Oui Non = Non; Non Oui = Non; Non Non = Oui. Et c'est alors l'occasion de découvrir quelque chose de plus profond, la multiplication des sens, qui se cache dans ces règles, et qui devient plus évident quand on écrit cela avec les signes, c'est-à-dire donc ce qu'on appelle les nombre (+1) pour Oui et (-1) pour Non. Cela donne alors : (+1) x (+1) = (+1); (+1) x (-1) = (-1); (-1) x (+1) = (-1); (-1) x (-1) = (+1).

Ainsi donc, on apprend au passage que l'opération de composition nommée "rond" ou "o", qui est celle impliquée dans ces combinaisons des Oui et Non, est fondamentalement la même chose que ce que nous concevons intuitivement comme la "multiplication". On peut d'ailleurs définir très précisément cet opérateur "o" ("rond") ou cette multiplication "x" comme un connecteur logique dont la table de vérité n'est autre que la règle de logique ou la règle des signes examinée plus haut :

Connecteur multiplication ou signification ou équivalence

Il est intéressant de remarquer que cette table de vérité du connecteur "multiplication" n'est nulle autre que celle du connecteur "équivalence logique". S'il y a un connecteur qui doit être la définition de la notion de sens ou de signification, c'est bien de celui de l'équivalence logique. Autrement dit, "Avoir le même sens", c'est "Etre logiquement équivalent", et vice-versa.

C'est donc la multiplication qui se cache en fait dans la combinaison des mots pour faire des phrases. Autrement dit, on additionne physiquement les mots, mais on multiplie les sens (ou significations) des mots ainsi enchaînés pour obtenir le sens (ou signification) de la phrase, comme dans les exemple élémentaires ci-dessus:

Vrai Vrai = Vrai ; "une vraie vraie chose est une vraie chose"
Vrai Faux = Faux ; "une vraie fausse chose est une fausse chose"
Faux Vrai = Faux ;"une fausse vraie chose est une fausse chose"
Faux Faux = Faux ;"une fausse fausse chose est une vraie chose"

C'est pourquoi donc très naturellement, comme avec les fonctions F et G définies plus haut (c'est-à-dire 2X et 3X), nous disons par exemple "deux enfants" ou "trois douzaines", ce qui signifie une multiplication du sens "deux" par le sens "enfant" pour avoir le sens "deux enfants", ou de "trois" par "douze" pour avoir "trois douzaines". C'est aussi la raison pour laquelle très intuitivement en algèbre, on a compris que pour dire axb, il suffit de dire ab comme dans "2X" ou "deux enfants", sans indiquer explicitement le signe de la multiplication entre les sens des deux facteurs pour avoir le nouveau sens. Comme par exemple aussi dans "vraie fausse chose", il n'est pas nécessaire de faire figurer explicitement un signe de multiplication entre les trois mots "vraie x fausse x chose". Et si même on juge nécessaire de le faire, alors dans ce cas on effectue simplement une multiplication des sens avec les mots : "vraie", "x", "fausse", "x", "chose", donc une multiplication qui porte entre autres choses sur la multiplication elle-même.

Bref, dans toute phrase (quelle soit scientifique ou du langage courant), on effectue simplement la multiplication des sens, qui s'applique à toute notion et à toute chose, que ce soit "2", "3", "Deux", "Trois", "Douze", "a", "b", "X", "Nombre", "Fonction", "Enfant", "Oui", "Non", "Vraie", "Fausse", "Composition", "rond", "o", "multiplication", "x", "Chose", etc. Derrière cela se cache la vérité très profonde mais ignorée que "Toute chose est un nombre", que je ne développerai pas ici, car cela nous conduirait très loin. Mais il suffit d'avoir démontré que "Le contraire de toute vérité est toujours une autre vérité" (ou simplement que "Tout est vrai"), pour avoir démontré aussi que la phrase "Toute chose est un nombre" est vraie. Et alors on comprendra pourquoi vraiment tout se ramène à une multiplication des sens. C'est l'occasion de dire aussi que dans une langue bien faite (ce qui n'est hélas le cas d'aucune langue actuelle, voir le document "La question de Dieu et du Diable aujourd'hui), on parlerait comme on fait la mathématique, et on ferait la mathématique comme on parle, y compris quand on parle de Dieu ou du Diable !

La troisième valeur de vérité et la physique

Aristote et l'"au-delà"...

On appelle une contradiction le fait d'affirmer à la fois une chose A et sa négation, non-A. Ainsi donc, la phrase "Il pleut ET Il ne pleut pas" est une contradiction. Et si je parle d'un "humain qui est un non-humain", je définis une chose A qui est "contradictoire".

Mais il faut beaucoup se méfier de ce qui paraît contradictoire, car une "contradiction" peut simplement traduire une certaine réalité, qui peut être cachée comme être très évidente. Derrière la "contradiction" d'un "humain qui est un non-humain" peut se cacher simplement un humain qui vient par exemple d'avoir un accident mortel sur autoroute. Il vient de quitter le monde des humains pour entrer dans le monde des morts. Et pourtant, il est difficile de ne pas parler de lui comme d'un humain.

Aristote (à qui on doit par exemple le principe de non-contradiction), est à la fois un humain, car il appartient à la race humaine, et à la fois poussière (donc un non-humain), car il y a très longtemps qu'il est mort. Et qu'il n'interdise surtout pas la possibilité qu'il puisse en ce moment vivre dans un autre monde (dans notre non-monde ou notre anti-monde), ou de nouveau dans ce monde dans un avenir.

Voilà donc pourquoi la notion d'un "humain non-humain" ou d'un "mort-vivant" n'est pas si absurde que cela. Je répète ceci : La contradiction est une chose, mais nier une possibilité ou une réalité en est tout une autre !

Déterminisme et indéterminisme

Une mauvaise compréhension de la réalité (à cause d'une mauvaise logique ou d'une logique très faible) conduit à appeler "contradiction" des situations qui invitent simplement à comprendre qu'une autre réalité existe, ou qu'une troisième réalité existe, autre que deux que l'on croyait être les seules possibles. Le problème par exemple en physique du chat de Schrödinger est un exemple typique du problème du "mort-vivant". Il s'agit d'une expérience mentale, portant sur les lois de la nature telles qu'elles se présentent dans le monde de l'infiniment petit (le domaine de la mécanique quantique), et qui déroutent la logique courante, qui est celle des échelles de grandeur ordinaires. A cette échelle, les lois sont dites "déterministes", ce qui signifie par exemple pour une voiture roulant sur une autoroute, que l'on peut connaître très exactement et à la fois sa position, sa vitesse, bref tous les paramètres de son mouvement avec la précision que l'on souhaite. Cette évidence à l'échelle courante est prise en défaut dans le monde de l'infiniment petit, où il faut abandonner la logique déterministe pour une logique probabiliste. Transposée à notre échelle, cela signifie qu'on ne peut pas dire exactement où se trouve une voiture sur une autoroute, ni sa vitesse, etc. Mais on dira qu'il y a telle probabilité (par exemple 50%, c'est-à-dire "une chance sur deux", ou 75% ou 99%) qu'on la trouve entre telle position et telle autre, avec telle vitesse, etc.

L'événement qu'est la rencontre entre particules
en un lieu précis, à un moment précis, avec des paramètres de mouvement précis
est une affaire de probabilité.
A plus forte raison ici particule et anti-particule, car la durée de vie de l'une dans notre monde est très limitée,
comme si "quelque chose" interdit aux particules opposées de coexister dans notre monde.
Mais en fait les mondes sont séparés comme les deux voies de l'autoroute,
la particule et son anti-particule évoluant chacune dans son monde;
quand l'une se trouve par "erreur" dans le "mauvais" monde,
tel un conducteur consciencieux, qui s'étant aperçu qu'il a pris l'autoroute à contre-sens,
s'arrange pour changer de voie au plus vite ! pour éviter la "catastrophe".

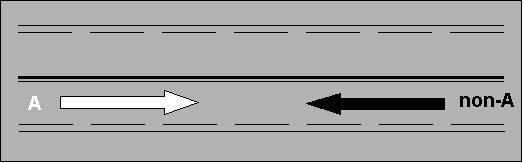
Dans la logique de la mécanique quantique, l'événement qu'est le choc entre les deux voitures venant en sens inverse sur la même voie de l'autoroute
est une question de probabilité.

Le problème du "mort-vivant"

En appliquant la logique quantique aux réalités courantes, si par exemple deux voitures roulent en sens inverse l'une par rapport à l'autre sur la même de l'autoroute, il est impossible de dire avec exactitude si le choc aura lieu, où exactement, quand, avec quelle vitesse, avec quelle énergie (donc avec quelle violence), etc. Dans la réalité (c'est-à-dire l'expérience que nous avons de la circulation à notre échelle), on peut avoir ces renseignements avec une très grande exactitude, et même prédire la mort des occupants des véhicules avec une très grande précision. En effet, le choc frontal très violent est inévitable entre deux voitures roulant très exactement dans l'axe, en sens inverse l'une de l'autre, chacune à 130 km/h. On peut avec une caméra de surveillance sur autoroute ou avec un radar mesurer avec précision ces paramètres et prévoir ce qui va se passer, à quel endroit précis et à quel moment. Et on peut dire avec certitude que ce choc ne laissera aucune chance de survie aux conducteurs, et que sortir vivant de cette affaire relève du miracle !

Autrement dit, pour les conducteurs, le choix entre les deux possibilité mort et vivant est net, et c'est le choix "mort". Quoique très improbable et relevant du miracle, la possibilité "vivant" existe aussi; mais il est exclu dans la logique courante de parler "vivant ET mort" (c'est-à-dire "vivant ET non-vivant"), ou de parler de "NI vivant NI mort". Le troisième état est carrément inacceptable, car selon la logique bivalente (ou logique binaire, la logique reposant sur le "modèle à deux"), on est SOIT vivant, SOIT mort, mais pas les deux, ou ni l'un ni l'autre ! Même si le langage courant nous amène à qualifier l'état de coma comme un état "entre la vie et la mort", pour la logique binaire, être dans le coma c'est être encore vivant un point c'est tout. Et toujours dans cette logique, ou l'on sort du coma ou l'on reste dans cet état, sinon alors c'est qu'on est mort tout simplement. Et si on est mort, alors c'est qu'on n'est plus vivant !

Mais le problème qui se pose ici n'est pas une discussion sur comment qualifier un état comme le coma, mais un problème plus profond et élémentaire, qui est simplement de savoir si on peut être à la fois "vivant ET mort", ou encore si pour un humain, on peut dire qu'il n'est "NI mort NI vivant". Quand dans l'Evangile (Jean chapitre 11) Lazare l'ami de Jésus fut emporté par la mort, Jésus en parla comme d'un sommeil duquel il va le tirer, ce qui étonna ses disciples. Selon la logique de ses disciples qui raisonnaient en "SOIT mort SOIT vivant mais pas les deux", si on dort, on n'est donc pas mort, et on peut se réveiller seul, sans avoir besoin de Jésus pour se réveiller. Mais Jésus raisonnait manifestement avec une autre logique qui admet une troisième vérité. Et le parlant de ses ancêtres Abraham, Isaac et Jacob, Jésus dit à ses contradicteurs (qui niaient la possibilité de la résurrection) que pour Dieu ils sont vivants (Luc 20 : 34-40). On ne s'étonnera donc pas que les affaires de Dieu et celles des sciences actuelles soient réputées si incompatibles. C'est fondamentalement une affaire de logique, et très précisément encore, une affaire de négation ! C'est l'obligation de trancher entre deux choses A et B qui pose en fait problème, comme ici entre vie et mort. La négation dans notre logique ou expérience courante doit obligatoirement trancher, elle doit être binaire ou booléenne, et c'est cela le fond du problème.

Si on a une décision à prendre, par exemple s'il faut avec sa voiture emprunter une autoroute ou prendre une route nationale distincte de l'autoroute), on ne peut pas être à la fois sur l'autoroute et sur la route nationale, c'est-à-dire ne pas être sur l'autoroute. De la même façon, ou bien on a été un passager du vol AF 447 qui s'est accidenté entre Rio et Paris, et dans ce cas on est une victime de l'accident; ou bien on n'est pas un passager de ce vol, et dans ce cas on n'est pas une victime de l'accident. Mais la logique actuelle interdit qu'on soit les deux à la fois, que l'on moitié-moitié ou un pourcentage de chaque (25% et 75% par exemple), ou que l'on ne soit ni l'un ni l'autre. C'est cela qui est actuellement inconcevable et qui est l'objet du fameux principe de non-contradiction.

On peut ne pas savoir avec précision si une personne a embarqué à bord du vol ou non, car elle peut avoir changé d'avis et être allée quelque part jouer au poker avec des amis. Dans ce cas il y a une certaine probabilité (1%, 25%, 50%, 75%, 99%, etc.) qu'elle ne soit pas à bord de ce vol. Mais la logique courante met cette probabilité sur le compte de l'ignorance, et cette probabilité ne signifie pas que la personne puisse être à la fois passagère de l'avion et non-passagère de cet avion, qu'elle peut être dans l'avion à 10 000 mètres d'altitude et avoir un pied sur le sol, ou qu'elle soit sur le sol mais un pied dans l'avion ! Tout cela est impossible et absurde dans la pensée actuelle.

L'affaire du "chat de Schrödinger" appelle une autre logique

C'est donc le fond du problème et c'est la question qui se pose au sujet de l'affaire du chat de Schrödinger. Dans le domaine de l'infiniment petit, il semble que ce ne soit pas une simple question d'ignorance ou d'incapacité de notre part de connaître une réalité, mais que la réalité soit intrinsèquement ainsi, elle est de nature probabiliste, indépendamment de notre faculté ou capacité de savoir. Dans cette logique quantique (de l'infiniment petit), être est passager ou non de l'avion est une affaire probabiliste. Et une fois descendu de l'avion, être ou pas un usager de l'autoroute est une affaire de probabilité, de même que la position de la voiture sur l'autoroute, sa vitesse, le moment (l'heure exacte), etc. Le choc avec une autre voiture est une affaire de probabilité, de même que l'état de mort ou de vivant du conducteur, etc. C'est pourquoi donc si on fait dépendre la vie d'un chat de ce qu'un événement quantique aura lieu ou non, on aboutit à une situation où l'on doit dire que le chat est mort-vivant ! On résout (ou plutôt on croit avoir résolu) ce paradoxe (cette "contradiction") de diverses manières, dont l'une est de séparer les échelles de l'infiniment petit et de l'infiniment grand (ou de l'échelle ordinaire), en prenant acte de leurs réalités "incompatibles". Ainsi donc, il faut simplement renoncer à concilier à tout prix la mécanique quantique et la relativité, respectivement la physique de l'infiniment petit et de l'infiniment grand. Une autre solution classique consiste à évoquer le rôle perturbateur de l'acte d'observation ou de mesure dans ce qu'on veut observer, ce qui entraîne une incertitude donc le phénomène de probabilité. Une approche voisine est de parler du rôle de la conscience du physicien ou de celui qui observe ou mesure. Et enfin une autre solution consiste à voir dans cette contradiction l'existence d'"univers parallèles" ou d'"univers divergents": dans l'un le chat est vivant et dans l'autre le chat est mort.

Mais la vérité est tout cela à la fois ! c'est-à-dire chacune de ces solutions est une partie de la vérité ! Et la vérité totale est simplement que l'on doit comprendre la réalité avec toutes les logiques, et pas seulement avec la logique binaire ! Autrement dit, il faut abandonner le principe de non-contradiction et la négation binaire (la négation qui tranche) qui lui est forcément associée, au profit du principe d'alternation, avec sa conception de la négation, qui est simplement l'alternation. Celle-ci fait la place à une troisième vérité, et même à une quatrième, une cinquième, une infinité ! La logique binaire suffit pour beaucoup d'usages courants. Mais elle montre ses limites face à une infinité d'autres usages, tout aussi courants.

En effet, il n'est pas nécessaire daller dans l'infiniment petit pour trouver des situations du genre chat de Schrödinger. Ces situations se posent à l'échelle ordinaire, mais simplement on les refuse, on a fait le choix philosophique de les déclarer d'office absurdes, impossibles, ou contraires à la science ! Le problème de l'ami de Jésus (à savoir de Lazare) et celui du chat de Schrödinger sont simplement le seul et même problème ! Les deux posent le problème du mort-vivant, la possibilité qu'un même être soit mort vu dans un monde donné, mais vivant vu dans un autre monde ! C'est aussi banal que quelqu'un qui quitte une pièce d'une maison pour se rendre dans une autre pièce de la maison. Il est de ce fait non-existant dans la pièce de départ, mais existant dans la pièce d'arrivée. Et il peut revenir dans la pièce de départ. C'est la même chose s'il quitte une ville pour une autre (en faisant un voyage sur l'autoroute), un pays pour aller à un autre (en voyageant en avion), etc. A chaque fois, il "meurt" en un sens faible du terme dans un contexte, et "revit" dans un autre contexte. Son retour dans le contexte de départ est une "résurrection" en un sens faible du terme. Mais s'il lui arrive un accident mortel pendant le parcours, alors son voyage se trouve simplement être beaucoup plus grand et son retour long, sauf si nous trouvons le moyen de le rendre court. C'est simplement ce que nous appelons la "mort" à proprement parler. Mais dans l'absolu, ceci répond à la même logique que ces expériences banales de la vie. Nous refusons simplement d'appeler "voyage" la "mort", et quand nous employons les expressions comme "A a fait un long voyage pour aller au royaume des morts", "A nous a quitté", ou "A est allé dans l'au-delà", etc., ce n'est en général qu'une "métaphore", et donner à cela exactement le même sens que le fait de quitter une ville pour une autre, relève du domaine de la croyance.

Le problème du chat de Schrödinger ne se pose pas que dans l'infiniment petit, mais aussi dans des réalités et expériences des plus banales de la vie, comme ... la mort ! Le problème est donc plus philosophique que scientifique à proprement parler. Sinon, dans l'absolu, la science ne s'oppose pas du tout à la possibilité que A puisse être à la fois mort et vivant, que deux choses contraires A et non-A puissent être vraies en même temps. Elle ne s'excluent que dans un contexte donné, mais pas dans l'absolu. On conçoit que qu'on ne puisse pas être et ne pas être à la fois dans une même pièce à un moment donné, dans une même voiture, sur une même autoroute, dans un même avion, dans une même ville, etc., mais dans l'absolu on est et on n'est pas à la fois ! Dans un contexte donnée, la vérité contraire est simplement masquée, imperceptible ou potentielle, ce qui ne veut pas dire que ce n'est pas une vérité. Ce n'est pas parce qu'on ne perçoit pas une chose dans un contexte qu'elle n'existe pas dans l'absolu ! Et puis la même chose peut tout à fait exister dans ce contexte mais sous une autre forme. Ainsi par exemple, une personne qui marche, parle et rit dans un certain monde (comme elle se comportait dans le nôtre), existe dans notre monde sous la forme d'un mort ou d'un cadavre. Ici elle n'est qu'un souvenir, une chose abstraite, mais ailleurs, elle est une chose concrète, que l'on peut voir, toucher ou entendre ! La science ne s'oppose pas à cela, mais c'est nous qui refusons la science qui dit cette simple vérité. Nous avons fait le choix de nous enfermer dans principe de non-contradiction, alors qu'il existe bel et bien une vérité au-delà de ce principe, et qui n'est pas obligatoirement une contradiction. La contradiction est une chose, dis-je, mais nier une réalité en est tout une autre !

Il y aurait encore beaucoup à dire !

Un aspect caractéristique de l'alternation est que toutes les notions sont synonymes, car une chose B n'est qu'une autre manière de parler d'une autre chose A; B n'est qu'une autre manière d'être de B. C'est pourquoi dans le texte la science de l'alternation (la Science de l'Existence) on verra très souvent alignés des termes comme synonymes, pour indiquer qu'il faut faire une relation entre eux. Cela peut être très déroutant pour un esprit habitué à fonctionner avec la négation, dont la nature est de séparer les choses, au point de briser leur unité et de rendre inintelligible la relation très intime qu'elles entretiennent. On parle de mille choses différentes : A, B, C, D, E, ... sans savoir qu'on parle de la même choses, de différents aspects d'une seule et même chose. Pour reprendre l'exemple du Cône plus haut, c'est le même objet qui vu sous un angle donné et suivant une certaine projection est appelé Cercle ou Disque. Mais le même objet vu sous un autre angle ou suivant une autre projection, est appelé Triangle (plein). Il y a des contextes où il faut séparer les notions de Cercle et de Triangle, comme choses ou notions à part entière, indépendantes, et à prendre en elles-mêmes comme telles. Mais il ne faut pas perdre de vue leur unité aussi, et savoir qu'il y a des contextes où Cercle et Triangle sont une certaine même chose nommée Cône, qui répond à la propriété "Cercle ET Triangle". Il y a des domaines où il faut distinguer les notions de Cycle et de Nombre, et d'autres où il est très important de comprendre qu'on parle de la même chose qui est donc "Cycle ET Nombre" ! Il y a des domaines où il faut séparer Nombre et Fractale, Fractale et Modèle, Modèle et Symétrie, Symétrie et Egalité, Egalité et Equivalence, etc. Mais il y a des domaines où il est très, très important de comprendre qu'on parle aussi finalement de la même chose !

Et quelle que soit la chose A dont on parle, il est extrêmement important de savoir que ce n'est qu'une facette d'une seule et même Chose, à savoir l'Univers ! Autrement dit, l'Univers U est la Chose, qui est : A ET B ET C ET D ET E ET F..., bref qui est toutes choses prises individuellement (c'est-à-dire en tant que ses éléments), et toutes choses prises collectivement (c'est-à-dire en tant leur ensemble). L'Univers est le TOUT au plein sens du terme, la Chose qui est l'Union même de toutes choses, qui les rend équivalentes, car "L'Univers ne fait pas de préférence..."

Einstein disait : "Dieu ne joue pas aux dés", et par Dieu il faut entendre l'Univers, et il avait raison ! L'Univers ne joue pas aux dés, il ne tire pas au sort pour savoir laquelle de ses infinités des choses sera la gagnante absolue, au détriment des autres. Il ne tire pas au sort pour savoir laquelle va exister et laquelle ne va pas exister, ou laquelle sera plus importante que toutes les autres. L'Univers est de fait la plus importante des choses, mais il se serait pas l'Univers sans les choses qui le constituent et le font ! Et s'il manque la moindre petite chose, alors il n'est plus le TOUT, donc l'Univers digne de ce nom. "Il faut de TOUT pour faire un Univers", dis-je. Toute chose est donc importante. La Différence est nécessaire pour la Diversité des choses et des rôles, mais l'Egalité est nécessaire aussi pour que justement toutes les choses puissent former une seule d'entre elle, qui porte l'attribut suprême : TOUT ou UN, et qu'on appelle l'Univers pour cela ! Et comment rendre tout Différent mais en même temps Egal ?

La solution est simple : l'alternation ! Toutes les choses sont différentes et jouent différents rôles, mais les rôles ALTERNENT, une chose donnée change de rôle, donc devient une autre, tandis qu'une autre devient ce qu'elle était. Tout se recycle, d'où l'importance de la notion de Cycle. L'Univers change donc infiniment, il se recycle sans cesse, et pourtant reste globalement égal à lui-même. "Rien ne se perd, rien ne se crée, tout se transforme dans l'Univers", dis-je. Une chose donnée devient successivement toutes les autres, et parcourt le Cycle de l'Univers. Le Cycle terminé, il faut recommencer. Tout cela fait que globalement les choses sont égales, elles sont équivalentes, il n'y a pas de préférence pour l'une au détriment des autres, la différence et la préférence n'est que ponctuelle, vraie dans un contexte donné. Il n'y a donc pas de prédilection, pas même pour l'Univers !

En effet, ce mot (comme le mot Dieu) est comparable au mot Président; ou plutôt, la notion de Président est une imitation du Modèle général qu'est Dieu... c'est-à-dire donc l'Univers. Le Président est toujours le plus important de tous les citoyens, il y a une énorme différence entre lui et les autres, ce qui peut être inquiétant, quand par exemple il ressemble à l'actuel Omni-Président de la république française, Nicolae Ceauseskozy... Mais heureusement, cela ALTERNE, et ce n'est pas toujours le même qui est le Président, et théoriquement tout citoyen peut devenir Président, il lui faut être candidat au poste. C'est en ce sens que finalement tous les citoyens sont égaux, même si à chaque moment ils sont très différents. L'égalité sera d'autant plus parfaite que l'alternation est parfaite, c'est-à-dire que le cycle fonctionne bien (dans cet exemple le cycle présidentiel). Le Président a un grand pouvoir et est supérieur au citoyen lambda, mais en vertu de l'alternation, le citoyen lambda est aussi potentiellement Président, et à l'échelle de l'Univers cela finit toujours par arriver ! Tout citoyen est égal au Président en ce sens-là. C'est ainsi que toute chose est l'Univers, car toute chose finit par s'asseoir sur le trône de l'Univers et porter le titre "Univers" ou... "Dieu".

L'alternation n'est prise en défaut (donc l'inégalité ou la différence ne règne) que dans des mondes donnés, dans des contextes donnés. Les phrases "Je ne suis pas le Président de la république" ou "Je ne suis pas Dieu" (c'est-à-dire donc "Je ne suis pas l'Univers"), ne vraies que ponctuellement, contextuellement, dans un monde comme le nôtre par exemple, qui a perdu le paradis nommé l'alternation, et où l'on a toutes les peines à comprendre que cette vie n'est qu'une parmi une infinité d'autres. Il y a eu une vie avant, et il y aura une après, qui peut être meilleure ou pire ! Si on veut une meilleure, il faut se porter candidat maintenant... il faut s'engager vers la voie du retour vers le trône de Dieu (de l'Univers je veux dire...) dans la prochaine vie, ou au contraire préférer un enfer pire que celui qu'a été ce monde.