Le Langage universel des ensembles
Chose, Ensemble, Univers, Existence
La
notion d'ensemble est l'une des notions les plus
intuitives et naturelles qui soient;
tout le monde
utilise très naturellement le langage des ensembles.
Dire par exemple : "les humains", c'est parler d'un ensemble,
celui des humains;
et dire : "un humain", c'est parler d'un élément
de cet ensemble, mais aussi d'une partie de cet ensemble,
parce que la matière qui constitue cet humain est une
partie de la matière qui constitue toute l'humanité.
Et l'humain en question est à son tour un ensemble fait
de ses parties et de ses éléments,
dont les cellules, les molécules, les atomes, les particules,
etc.,
qui à leur tour sont des ensembles faits d'autres choses,
et ainsi de suite.
Et l'ensemble qu'est l'humanité fait partie de l'ensemble qu'est
le système solaire,
lui-même faisant partie de l'ensemble qu'est notre galaxie
la Voie Lactée,
elle-même faisant partie de l'ensemble qu'est NOTRE univers,
et ainsi de suite.
Ainsi est la notion universelle des ensembles, c'est elle qui
permet de parler de TOUT !
Le langage des ensembles est le langage même de l'Univers,
et l'Univers est
justement le plus grand des ensembles : l'Ensemble de toutes
les choses,
l'ensemble dont les éléments (et aussi les parties)
sont appelés les CHOSES.
La notion universelle d'ensemble s'oppose radicalement à l'actuelle notion
axiomatique
d'ensemble (w),
qui est purement technique, abstraite, coupée de la réalité,
de l'Univers,
du monde physique et de sa logique !
Ce langage axiomatique des ensembles
a été mis au point au début du XXème siècle
à cause des paradoxes découverts
dans la théorie des ensembles de Cantor.
Mais les paradoxes viennent
du Problème de la Négation,
et surtout de ce que la science actuelle ne repose pas sur l'Univers
au
sens le plus TOTAL du
terme.
C'est justement ce grave défaut des sciences actuelles qu'il faut corriger
en faisant désormais toute la science
dans un langage unique et universel :
le Langage universel des ensembles, le Langage de l'Univers TOTAL.
|
Le
Langage de l'Univers TOTAL
--> Le
mot CHOSE, le mot clef du langage universel des ensembles
--> La
définition des notions d'ENSEMBLE, d'UNIVERS et d'EXISTENCE
Le
Langage de la Nouvelle Mathématique et Physique
--> Le
langage scientifique doit être le langage NATUREL !
--> Une
notion PHYSIQUE et NATURELLE d'ensemble
--> Les
ensembles physiques sont TRANSITIFS !
Documents
associés :
Définition
des termes clefs de la Science Nouvelle
La
question d'EXISTENCE
(ou La définition
scientifique exacte de la notion d'EXISTENCE)
Le
Verba : la Langue du verbe Etre
Théorème
de l'Existence, Loi de l'Univers
Algèbre
universelle des ensembles
Langage
Chromatique de l'Univers
Codage
Universel
Le langage de l'Univers TOTAL
Le mot CHOSE, le mot clef du Langage universel
des ensembles

L'Univers a
son propre langage, le langage universel des ensembles,
que ce document fait découvrir. Parce que l'Univers (surtout
si l'on parle de l'Univers au sens le plus TOTAL du
terme) est unique, il faut aussi UN SEUL mot clef pour écrire
ce
langage, pour définir tous les autres mots de proche en proche. Un
très excellent candidat pour bâtir
est le
mot CHOSE, au sens le plus intuitif, général,
universel du terme. Un
autre très bon choix est le verbe ETRE (voir Le
Verba, la Langue du verbe ETRE).
Une chose est
TOUT ce dont on parle, TOUT ce que l'on conçoit, indépendamment
pour l'instant de toute question de l'existence de
la chose.
En ce sens par exemple, Dieu est une chose, peut importe ce qu'on entend par
là, et peu importe s'il existe ou non. On est justement en train de poser les
mots de base pour effectuer la science qui répondra
à cette question et d'autres. Le mot chose est
le mot par
défaut,
que
l'on
emploie
là
où
on n'emploie aucun autre, là où aucune autre précision n'est apportée, sauf
de dire qu'on parle d'une chose.
La
définition des notions d'ENSEMBLE, d'UNIVERS et d'EXISTENCE

Chose, Existence, Ensemble :
Trois manières différentes de dire la même Univers.
Partant
de ce mot chose, il faut très
rapidement définir les autres mots clefs fondamentaux de la
science, comme par exemple les notions d'ENSEMBLE, d'UNIVERS,
d'EXISTENCE
(le verbe EXISTER).
-->
Par définition, "Une chose est
un ensemble, si
on veut indiquer qu'elle est faite ou constituée d'aucune,
d'une ou de plusieurs
choses, appelées ses éléments". C'est
ainsi que le plus naturellement du monde nous concevons la notion
d'ensemble :
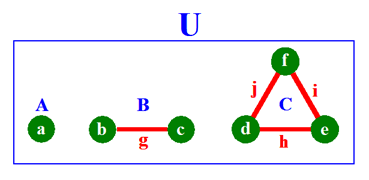
Une chose U, faite de plusieurs autres choses;
c'est la définition que la Science Nouvelle fait de la notion
d'ensemble, une notion physique !
Par exemple, U évoque ici un ensemble de molécules et d'atomes.
La
chose U ci-dessus peut être décrite
comme faite de trois choses
A, B, C,
donc comme un ensemble dont les éléments sont A, B, C;
cet
ensemble est noté : U = {A,
B, C}. Mais
la même chose U peut être décrite
comme faite de six choses
a, b, c, d, e, f, g, h, i, j;
donc comme l'ensemble de six éléments : U
= {a, b, c, d, e, f, g, h, i, j}. Les choses g,
h, i, j représentent
par exemple des liaisons entre des atomes b, c, d, e, f.
Et
enfin, la même chose U peut être
décrite comme faite d'une seule chose, à savoir U !
On a donc dans ce cas : U = {U}, c'est-à-dire
un ensemble à un seul élément.
Pour
aller plus loin dans la description de U, on
peut prendre en compte par exemple les "liaisons" entre les
molécules A, B, C,
ou l'espace dans lequel elles sont, qui les sépare mais
aussi les unit, exactement comme par exemple aussi g sépare b et c (ou h sépare d et e),
mais les unit aussi à la fois. U est
une modélisation simple de l'Univers et de
la notion d'ensemble qui est la sienne.
La notion
d'ensemble définie, il
est très aisé de définir scientifiquement
l'Univers, comme on ne l'a pas fait avec
une telle exactitude jusqu'ici, ou plutôt, comme on n'a
pas mesuré toute l'importance
de le faire et de bâtir toute la science sur cette définition
fondamentale (voir La
question d'EXISTENCE).
--> Par
définition, "L'Univers est la chose faites de
TOUTES les choses; l'Univers est donc l'ensemble de TOUTES les
choses." Définition
aussi simple que très puissante. Elle est de la plus haute
importance, car l'Univers va être l'objet central de toute la
nouvelle science, le chef d'orchestre de toute cette science,
celui sur lequel tout repose et autour duquel tout s'articule
!
Tel
qu'il est défini ici, cela signifie
tout simplement que les mots Univers et chose sont
la seule et même notion, l'une en tant qu'ENSEMBLE et
l'autre en tant qu'ELEMENT. Autrement dit,
la notion de chose posée comme point de départ
(donc le mot correspondant à la notion universelle d'élément étant
posé), l'Univers se définit en conséquence
comme l'ensemble associé
au mot chose, à savoir donc l'ensemble
de toutes les choses. Et à l'inverse, si c'est
la notion d'Univers qui était posée comme
mot premier (le mot qui correspond à la notion d'ensemble),
alors le mot chose (la notion d'élément associée
à cet ensemble) se définit en conséquence
ainsi : "Une chose est un élément de
l'Univers".
Ainsi
donc, chose ou Univers,
c'est exactement la même chose, vue
comme élément ou comme ensemble.
Pour le dire en termes de
physicien,
le mot chose est le quantum de
l'Univers (au sens de la physique
quantique), c'est-à-dire le mot qui désigne la plus
petite unité de matière ou
de substance de l'Univers.
TOUT et absolument TOUT est de cette substance fondamentale,
de cette matière universelle, désignée par le mot chose.
Nous
sommes maintenant capable de définir avec la plus grande précision
la très importante notion d'EXISTENCE :
--> Par
définition, "EXISTER, c'est être un élément
de l'Univers TOTAL, l'ensemble de toutes les choses; EXISTER,
c'est
donc être
tout simplement une chose." (voir
aussi La
question d'EXISTENCE).
Cette
définition de la notion d'existence est
d'une extrême importance. Il ne s'agit plus d'une notion philosophique,
vague, subjective, mais d'une notion objective, définie avec
exactitude, en relation avec l'Univers, lui-même
désormais défini avec la même exactitude. On peut maintenant
formuler le théorème fondamental de la Science Nouvelle, le
Théorème
de l'Existence : "Toute chose existe".
Ce
théorème est trivial, dans la mesure où il n'est qu'une autre
manière d'exprimer la définition de la notion d'EXISTENCE : "EXISTER,
c'est être
tout simplement une chose." Autrement dit encore,
du simple fait d'avoir défini l'Univers TOTAL comme
étant l'Ensemble
de toutes les choses, il en résulte immédiatement
que "Toute chose existe" dans cet ensemble, dans
l'Univers TOTAL donc.
|
Le
Langage de la Nouvelle Mathématique et Physique
Le
langage scientifique doit être le langage NATUREL !
Le
langage scientifique actuel part du principe que le langage
courant est imparfait, flou, ambigu, donc impropre
pour faire la science. Il faut donc bâtir (pense-t-elle)
un langage scientifique, rigoureux, qui ne souffre d'aucune
ambiguïté. Et
c'est vrai que le langage courant (et les langues courantes)
actuelle
est
très imparfait. Mais il n'a, heureusement, pas que
des défauts, et ses défauts ne sont du tout
pas là où les scientifiques le pensent ! L'idée
d'un langage scientifique rigoureux part d'une bonne intention,
mais pas à n'importe quel prix. Si c'est pour bâtir (comme actuellement) des
jargons, des langages ésotériques, abscons, hermétiques, compréhensibles
seulement par les spécialistes et les initiés, alors l'objectif
est raté ! Et s'il se trouve que ces jargons en plus sont coupés
de la réalité et contredisent l'Univers, la Nature, alors le
remède est finalement pire que le mal !

L'Univers est une affaire de TOUS.
La science a vocation à être universelle.
Par conséquent la
langage scientifique doit être universel, naturel, compréhensible
par tous.
Ce n'est pas ce genre de langage que ce tableau d'un "matheux"
traditionnel montre...
C'est ce langage ésotérique
et cabalistique que parlait autrefois le Fils
de l'homme.
Il est aujourd'hui un repenti, et parle le langage de l'Univers...
Outre
ses termes propres, le langage scientifique utilise beaucoup
de termes que le commun des mortels utilise aussi, par exemple
les mots ensemble, élément,
négation, contraire,
ordinal, cardinal, nombre,
relatifs, rationnels, irrationnels,
réel, imaginaire,
corps,
référentiel, mesure, énergie, puissance,
etc. Mais il
suffit aujourd'hui de prendre simplement un dictionnaire,
et de comparer les sens courants de ces mots et leurs sens
mathématiques ou scientifiques. Très souvent, ça n'a presque
rien à voir, comme par exemple les mots irrationnels, réels,
imaginaires... Et quand il y a quelque chose
en commun, il ne faut pas en déduire que la conception scientifique
est plus juste que celle courante !
Un exemple
très frappant est la notion d'ensemble.
Dans le langage courant, ce mot s'applique aussi bien aux
ensembles des nombres qu'à un être humain,
un ensemble
physique, faits d'éléments ou
de parties (là encore dans le sens courant)
comme la tête, le thorax, les bras, etc. Et la conception
courante et naturelle ne voit pas pourquoi quoi on ne dirait
pas "ensemble de tous les ensembles"
(ensemble actuellement interdit !), "ensemble
de tous les ordinaux"
(ensemble actuellement interdit !) ou "ensemble
de toutes les choses" (l'Univers TOTAL,
ensemble actuellement inconnu et indirectement interdit
!), comme on dirait tout simplement "ensemble
de tous les humains"
! Il y a donc un conflit entre la conception naturelle des
ensembles et la conception mathématique !
Comme
second très important exemple, on peut citer la très importante
notion de
CONTRAIRE. D'après
le dictionnaire Succès, par contraire il
faut entendre : "Différent au suprême
degré, opposé." Et pour le dictionnaire
Petit Robert le mot contraire signifie
: "Qui présente la plus grande différence
possible, en parlant de deux choses du même genre".
C'est la définition la plus intuitive et
la plus naturelle de la notion de Contraire.
Mais
pour les logiciens actuels,"Deux choses contraires sont
deux choses qui ne peuvent pas être vraies en même
temps, mais pouvant être fausses toutes les deux"...
Mais il s'agit hélas d'une très mauvaise
conception de la notion de contraire.
Car il suffit de bâtir la science sur l'Univers
TOTAL (bien
défini plus haut) pour s'apercevoir que dans
cet Univers, TOUTE chose est vraie, et
le contraire de
TOUTE chose aussi ! En disant une chose
qui revient à NIER l'Univers TOTAL et ses
lois, les logiciens, les mathématiciens et les scientifiques
actuels sont hélas dans l'erreur ! La bonne notion de CONTRAIRE,
celle que révèle l'Univers TOTAL,
est ce qu'on appelle actuellement notion d'"Opposé",
comme quand on parle des nombres opposés -3 et +3,
ou -9 et +9.
Et une chose et son contraires peuvent effectivement être
vrais, comme par exemple 0, qui est à
la fois négatif et positif.

Bref,
ici aussi, la conception intuitive et naturelle de contraire,
est de loin la meilleure comparée à la conception scientifique,
dite plus rigoureuse... La Science
Nouvelle redonne toutes ses lettres de noblesse au langage
courant et aux conceptions naturelles,
car elles sont les plus universelles, plus conformes à l'Univers
TOTAL, à sa nature et à son fonctionnement. Il suffisait
donc juste de redéfinir les mots du langage courant sur la
base de l'Univers TOTAL, pour corriger leur
défauts et leurs imprécisions, sans verser dans l'ésotérisme
qu'est le langage scientifique actuel, et qui de surcroît
se révèle le plus éloigné de la Réalité...
Une
notion PHYSIQUE et NATURELLE d'ensemble
La
notion d'ensemble est l'une des notions
les plus intuitives qui soient, et le langage des ensembles
est celui que tout le monde parle très naturellement.
Par exemple, le simple fait de dire "LES humains" c'est
parler d'un ensemble, celui de TOUS les humains. Et un
humain nommé Théophile par exemple est un élément
de cet ensemble. Et Théophile lui-même est
un ensemble fait d'une tête, de bras, d'un thorax,
etc., qui sont ses parties, mais aussi ses éléments.
La
notion universelle d'ensemble, qui est
celle de la Science
Nouvelle, est une notion PHYSIQUE, CONCRETE !
En effet, pour
définir la notion d'ensemble à partir
du mot chose, nous avons
utilisé l'expression très physique et
très concrète suivante : "FAIT de ...", "CONSTITUE
de...". Nous avons dit : "Un ensemble est
une chose faite (ou constituée)
d'aucune, d'une, ou de plusieurs choses, appelées
ses éléments".

La
chose U ci-dessus peut être décrite
comme faite de trois choses A, B, C,
donc comme un ensemble dont les éléments sont A, B, C;
cet ensemble est noté : U = {A, B, C}.
Mais la même chose U peut être
décrite comme faite de six choses a, b, c, d, e, f, g, h, i, j;
donc comme l'ensemble de six éléments : U
= {a, b, c, d, e, f, g, h, i, j}. Et enfin, la même
chose U peut être décrite comme
faite d'une seule chose, à savoir U !
On a donc dans : U = {U}, c'est-à-dire
un ensemble à un seul élément.
Cette
conception naturelle des ensembles (une
conception très physique, comme on
le voit) est radicalement différente de la conception
mathématique traditionnelle des ensembles. Dans cette
conception, seule une des différentes
descriptions de la chose U devra être
qualifiée d'ensemble U, par exemple U
= {A, B, C}, qui présente trois objets "séparés" A, B, C,
qui seuls ont le droit d'être appelés les "éléments" de
l'ensemble. Une "partie" ou "sous-ensemble" de U sera
par exemple l'ensemble des deux choses {A, B}.
Dans cette conception rigide (et très peu naturelle),
la chose B n'est pas une partie (ou sous-ensemble)
de U, car les choses b et c ne
sont pas des éléments de U.
Mais c'est {B} qui est un sous-ensemble
de U.
Et
on ne parle du tout du même ensemble U en
disant : U = {a, b, c, d, e, f, g, h, i, j}.
Mais si U est ainsi défini, dans
ce cas A, B, C ne
sont plus des éléments de U,
mais des sous-ensembles (parties) de U.
Et enfin, dans la conception traditionnelle des ensembles,
l'écriture U = {U} est proscrite,
car elle signifie que U est un élément
de lui-même. Mais ici, on dira seulement que U est
une partie de U, et pas un élément.
Dans
la conception mathématique traditionnelle, il faut
d'une manière très générale distinguer
les notions d'élement et de partie (sous-ensemble).
Ces deux notions ne sont synonymes que pour un certain type
d'ensembles, appelés les ensembles
transitifs. Mais dans la nouvelle conception des
ensembles, la conception naturelle (qui est celle des ensembles
physiques, comme l'exemple U ci-dessus),
c'est complètement l'inverse. En règle très
générale, les notions d'élement et
de partie sont la seule et même notion.
Les éléments d'un ensemble sont ses parties.
Et selon comment on décompose un ensemble en ses parties,
il a tels éléments ou tels autres, tel nombre
d'éléments ou tel autre, le cas échéant étant
qu'il a pour unique élément lui-même.
Et au besoin on choisira d'appeler "éléments" (au
sens traditionnel actuel du terme) une certaine décomposition
particulière mettant en évidence des parties
considérées comme "élémentaires" (les
plus "petites") ou comme des unités de l'ensemble.
Autrement dit, le terme "élément" signifiera : "petite
partie". C'est
donc nous qui décidons si une partie est suffisamment petite
pour
être
appelée élément.
C'est
par exemple nous qui décidons si les cellules d'un humain
sont des parties (terme général) ou des
éléments (pour signifier
"les
plus petites parties" de
l'humain), si la notion d'élément va
commencer avec les
molécules (encore plus petites
que les cellules), si elle va commencer
avec les atomes (encore plus petits que
les molécules), si elle va commencer
avec les particules (encore plus petites
que les atomes), etc. Mais on peut tout
aussi bien appeler "éléments"
les organes (plus
grandes que les cellules), et même carrément
les parties comme les bras, les jambes, l'abdomen, etc.
C'est nous qui décidons, tout comme c'est nous qui décidons
à partir de quelle valeur ou en dessous de quelle valeur
un nombre sera appelé grand ou petit : 1000 ? 1000000 ?
1000000000000000000 ? Ne nous rendons pas (avec un paradigme
de la Négation)
esclaves de limites uniques et rigides, comme si c'était
la seule possibilité ou seule vérité qui puisse exister.
Ainsi
donc, de même dans l'exemple de l'ensemble U,
selon l'usage que l'on veut en faire ou le point de vue où l'on
se place, on peut juger "élémentaire" la
décomposition U = {a, b, c, d, e, f, g, h,
i, j} ou U = {A, B, C}. Les notions
de partie et d'élément ne
doivent donc pas être
aussi rigides que dans la conception actuelle
des
ensembles.
La rigueur est
une chose, et la rigidité en est
tout une autre !
L'approche
des ensembles adoptée ici a pour but d'être
parfaitement fidèle à la notion physique
et naturelle d'ensemble, telle qu'elle fonctionne
dans l'Univers. Dans la conception traditionnelle,
on se préoccupe seulement de la relation entre un
ensemble U et les éléments
qui le constituent, et pas de comment sont faits ces éléments à leur
tour. Si l'on dit par exemple U = {A, B, C},
on ne se préoccupe en général pas de
comment sont faits A, B et C,
sauf en des cas où U est ce qu'on
appelle une structure (comme par exemple
les structures algébriques).
Mais
il est évident et très naturel de dire que si U est
un ensemble constitué de choses A, B, C,
alors tout ce qui constitue A, B et C constitue
aussi U ! Pour une conception parfaite (et
surtout naturelle) de la notion d'ensemble, la notion d'"élément
de U" doit donc aller au-delà des seuls éléments
A, B, C.
Et considérer les éléments (ou constituants) de A, B, C et
dire que ce sont aussi des éléments (ou constituants) de U transforme
automatiquement A, B, C en
parties de U. Ainsi donc, dans une notion
très générale et universelle d'ensemble, les notions de parties
et d'élément sont la même notion. On ne perd rien en généralisant
un concept, dans la mesure où le concept plus général englobe
l'ancien, et que l'on peut faire avec le concept général
tout ce qu'on faisait avec l'ancien.. Mais on perd toujours
en restreingant un concept, le concept restreint
ne pouvant
pas accomplir
tout ce que peut faire avec le général. On ne perd rien avec
une notion plus générale
d'élément, une
notion désormais synonyme de partie.
Avec U par exemple, A, B, C, a, b, c, d, e, f, g, h, i, j,
{A, B}, {A, C}, {a,
b, c},
U, etc., sont ses parties,
donc ses élements dans
le sens général du terme. On peut toujours, quand on veut
ou au besoin, restreindre cette notion générale pour retrouver
une notion restreinte d'éléments, qui ne considère comme
tels par exemple que A, B, C.
On peut donc faire avec cette nouvelle conception tout ce
qu'on faisait avec la conception traditionnelle. Mais la
nouvelle conception offre d'immenses nouvelles possibilités
(celles des ensembles physiques), que l'ancienne
n'offrait pas, et même interdisait, pour cause de paradoxes.
Mais justement les paradoxes venaient de cette conception
restreinte d'ensemble, qui n'est pas fidèle à l'Univers (au
sens le plus TOTAL du
terme), à sa nature, à sa logique et à son fonctionnement.
Les
ensembles physiques sont TRANSITIFS !
Une
propriété remarquable des ensembles
physiques d'une extrême importance est
qu'ils sont transitifs. Cela signifie
tout simplement que la notion d'élément et
de partie (ou sous-ensemble)
sont la même chose pour ces ensembles.
Nous avons posé les bases de cela dans le sous-titre
précédent.
Par
exemple, on peut tout aussi bien dire que le bras d'un humain est
un élément de son corps
comme dire que c'est une partie (ou sous-ensemble)
de son corps. Une branche d'un arbre est
tout aussi bien un élément de
l'arbre qu'une partie de
l'arbre. C'est nous qui
décidons donc de ce que nous allons appeler un élément d'un ensemble
physique ou une partie de
cet ensemble.
Cela offre une très grande liberté, souplesse
et confort dans le traitement des ensembles physiques,
mais aussi travailler avec eux est extrêmement
simple, naturel et très
intuitif. En effet, ils correspondent à notre
manière très naturelle de raisonner. La preuve
est que dans le langage courant on utilise très intuitivement
et très naturellement les mots élément et partie comme
des synonymes.
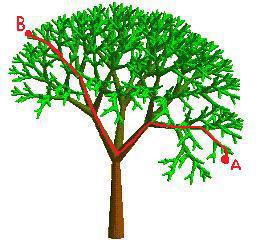
L'arbre,
un exemple simple mais très important d'enemble
physique,
qui illustre une propriété très importante
des ensembles physiques : la transitivité.
Cela signifie que les notions d'élément et de partie (ou sous-ensemble)
sont parfaitement synonymes.
Une branche de l'arbre par exemple est tout
aussi bien un élément de l'arbre qu'une partie de
l'arbre.
Cette propriété entre autres est celle de la notion d'ensemble
de la Science Nouvelle,
dont le langage est le langage universel des ensembles,
le langage des ensembles le plus naturel, aussi naturel qu'un arbre.
Tous les secrets
de l'Univers sont dans cette structure de l'arbre (voir L'Univers
fractal, l'Univers-Dieu).
|
|







