La
notion d'ensemble est
l'une des notions les plus intuitives, naturelles et universelles
qui soient, et pour cause : le langage
des ensembles est le langage même
de l'Univers !
Tout le monde raisonne très naturellement en utilisant
le langage
des ensembles.
Par
exemple, dire que "Théophile est un humain" c'est
dire que Théophile est un élément de
l'ensemble des humains. Dans cette simple
phrase est donc cachée la notion d'ensemble et
d'élément. Et dire que "Les
français sont des humains" c'est dire que
l'ensemble des français est un sous-ensemble de
l'ensemble des humains. Et dire que "Le
bras de Théophile est une partie de son corps",
c'est dire ce bras est un sous-ensemble de
l'ensemble qu'est le corps de Théophile.
Bref,
on ne peut pas s'exprimer et dire la moindre petite chose
que ce soit (et à plus forte raison faire la science
!) sans utiliser le langage
des ensembles. Ce langage est tout simplement UNIVERSEL !
On ne peut pas prétendre faire la science, étudier
et comprendre l'Univers,
si le langage cette science n'est pas le langage
universel des ensembles. Il
s'agit du langage même de l'Univers,
l'Univers TOTAL, l'Ensemble
de toutes les choses.
L'Univers
et la question de l'Ensemble Plein
C'est
en 1882 que Georg
Cantor a introduit la très importante théorie
des ensembles (w). Par "ensemble" il
entendait "un
groupement en un tout d'objets bien distincts de notre intuition
ou de notre pensée". On ne tarda pas à découvrir
des paradoxes (ou contradictions) dans cette théorie.
On affirma alors que les paradoxes sont dus au fait que Cantor
utilisait une notion d'ensemble dite "naïve", "trop
générale", "pas rigoureuse",
etc., ce qui signifie qu'elle n'est soumise à aucune "axiomatique".
On a mis au point diverses théorie axiomatiques des ensembles, la référence
en la matière étant la théorie des ensembles de Zermelo-Fraenkel
ou ZF (voir techiquement ce que c'est dans le document la Théorie
des univers).
Les
théories axiomatiques des ensembles actuelles ont ceci en commun
: elles travaillent en général avec un ensemble nommé l'ensemble
vide (l'ensemble n'ayant aucun élément) mais déclarent impossible l'existence
de son contraire, l'ensemble plein, l'ensemble
ayant TOUS les ensembles comme éléments, c'est-à-dire donc
l'ensemble de tous les ensembles. La raison
du rejet de l'ensemble plein est qu'il provoquerait des paradoxes.
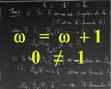

Vidéos
: 1) La
science exacte qui ment 2) Toute
la lumière sur les Paradoxes 2) L'Algèbre
du Cycle
Mais
en réalité, le problème vient de ce
que l'on fonctionne actuellement avec la Négation,
et de ce fait on
aborde très mal l'Univers,
les choses et les ensembles, la
science actuelle ne repose pas sur l'Univers TOTAL,
l'Ensemble de toutes les choses (voir
aussi La question d'Existence). C'est
l'ensemble
plein manquant lui-même, l'ensemble de toutes les ensembles !