L'Arbre de la Science

"Imaginez une science dans laquelle toutes les connaissances se rejoignent; imaginez une science dans laquelle toutes choses a sa place; imaginez une science avec laquelle toutes choses deviennent possibles."

La science qui englobe TOUT
La Logique de l'Arbre

Voir aussi :
Puzzle de l'Univers et visage de Dieu
L'Univers fractal, l'Univers-Dieu
Le secret pour faire la Science du Tout
Chose, Existence, Ensemble
Le Verba : la Langue du Verbe Etre

La science qui englobe TOUT...

Le sens éthymologique du mot "science" (du latin "scientia") est "connaissance". Selon le dictionnaire Succès (1987), une science est un "corps de connaissances constituées, articulées par déduction logique, et susceptibles d'être vérifiées par l'expérience". Quand au dictionnaire Robert (1995), il propose de comprendre par science "l'ensemble de connaissances, d'études d'une valeur universelle, caractérisées par un objet (domaine) et une méthode déterminés, et fondées sur des relations objectives vérifiables".

Le mot clef commun à toutes les définitions est le mot "connaissance". Et ce qui ressort de toutes les définitions est qu'une science est une connaissance ou un ensemble de connaissances, mais qu'un ensemble de connaissances n'est pas nécessairement une science. Donc par exemple la philosophie ou la religion n'est pas une science.

Et la question qui se pose maintenant est de savoir pourquoi l'ensemble de toutes les connaissances ne peut être unifié en une seule Science (en majuscule), répondant au cahier des charges définis ci-dessus ? Une Science dont l'objet (ou domaine) serait bien spécifié, dont le paradigme (le fondement philosophique) serait clairement identifié, et dont la méthodologie serait bien définie. Une telle entreprise est-elle si impossible que cela ?

Posons le problème autrement, en utilisant une image simple qui parle à tous : Pourquoi la science (et à plus forte raison la connaissance en général) est-elle obligée d'être une foret nommée sciences au pluriel, au lieu d'être simplement un Arbre nommé Science au singulier , dont les différentes sciences ne seraient que des branches ?

Vous êtes invités ici à comprendre pourquoi une telle entreprise a été impossible jusqu'à maintenant, quels étaient les obstacles, quel est le fond du problème, comment il se résout. Le principal obstacle se résume à une seule chose : le principe de non-contradiction. Cet obstacle levé , il en résulte une nouvelle science coginitive, une science très fondamentale, qui est la Science Nouvelle.

Son domaine et objet d'étude ? La notion d'EXISTENCE. Ou plus précisément, son domaine d'étude est la notion fondamentale de chose, et son but premier est de démontrer que "Toute chose existe" (Théorème de l'Existence), donc que les notions de chose et d'existence sont parfaitement synonymes. Sa philosophie (ou logique ou paradigme) ? Justement le contraire du principe de non-contradiction, qui est un élément clef tout le raisonnement actuel (voir La fin de la science aristotélienne et le Théorème pour public initié). Sa méthodologie ? La théorématique, par opposition à l'actuelle axiomatique, et aussi à l'empirisme traditionnel, c'est-à-dire la doctrine habituelle selon laquelle une théorie contredite par l'expérience est obligatoirement fausse. Ceci est une forme d'expression du seul et même principe de non-contradiction.

La théorématique ne pose pas en règle la contradiction avec la réalité ou la vérité, mais fait simplement prendre conscience du fait qu'une théorie peut très bien être parfaitement conforme à la réalité, et pourtant être déclarée contradictoire avec cette réalité. Tout dépend simplement de la logique avec laquelle on évalue la conformité à la réalité. On peut conclure à la contradiction ou à la non conformité à avec la réalité, alors qu'en réalité c'est la logique elle-même qui est contradictoire. C'est donc elle-même qui produit la contradiction qu'elle mesure. C'est exactement comme mesurer une longueur avec une règle faussée. On trouve alors la longueur fausse ou non conforme à ce qui était attendu, alors qu'en réalité la longueur est juste mais la fausseté vient au contraire de l'instrument de mesure ! C'est exactement aussi comme un daltonien qui déclarerait qu'un objet n'est pas de la bonne couleur, alors que c'est sa vision qui est en cause.

Cela signifie d'une part que la science actuelle est entièrement refondée sur de nouvelles bases, mais aussi que la nouvelle science permet désormais d'accéder à toute la vérité, à toute la réalité. Bref, tout ce qui était impossible avec les sciences actuelles devient maintenant possible dans la Science Nouvelle. Tout y a maintenant sa place, et en particulier Dieu. C'est pourquoi donc cette nouvelle science sera souvent qualifiée de Science de Dieu.

La Logique de l'Arbre

On utilise bien le langage de l'arbre pour parler d'une science particulière, les mathématiques ou les maths par exemple... La géométrie, l'algèbre, l'analyse, etc., sont des branches des mathématiques, ce qui laisse penser que les mathématiques sont un arbre unifié... Et les branches ont elles-mêmes leurs sous-branches, qui ont à leur tour leurs sous-branches, etc.

Si les "branches" des mathématiques constituent des domaines plus unifiés (donc qui peuvent être vraiment appelés des arbres), les mathématiques dans leur ennsemble ont beaucoup de mal à perdre ce "maudit" pluriel pour s'appeler simple LA Mathématique ! Pour qu'un domaine puisse être tout entier comparé à un arbre (et non pas à une forêt d'arbres séparés ou même carrément à une jungle épaisse où l'on s'y perd, comme justement dans les mathématiques !), il faut qu'il puisse être unifié en un tronc unique, c'est-à-dire caractérisé par un domaine unique (défini par un ensmble précis de mots clefs fondamentaux, voire un seul !), un paradigme unique (sa philosophie, et plus précisément sa logique fondamentale), et sa méthodologie (qui est la manière dont tout cela s'articule pour engendrer les connaissances de tout le domaine).

Pour prendre l'exemple des mathématiques, la théorie des ensembles de Georg Cantor (1845-1918) a été grand espoir d'unifier tout ce qu'on peut dire en mathématiques en une seule théorie. Le domaine ou objet unificateur dans ce cas est la notion d'ensemble. Et à vrai dire, il est difficile de trouver plus unificateur qu'un mot comme la notion d'ensemble, qui de part son sens même signifie réunion, union ou unification ! Et le paradigme de la théorie des ensembles est simplement aussi le paradigme de toute la science actuelle. Il s'agit simplement de la logique aristotélienne (voir La fin de la science aristotélienne), et plus précisément encore d'un de ses principes fondamentaux, le principe de non-contradiction, qui est la base même de tout le raisonnement scientifique, d'Aristote à nos jours. Et enfin, la méthodologie actuelle de la théorie des ensembles et des mathématiques est l'axiomatique. Cette méthodologie est étroitement liée au principe de non-contradiction, puisque le but d'un système d'axiomes et la condition primordiale qui est exigée de ce système est d'être non-contradictoire. Qu'on enlève le principe de non-contradiction et qu'on le remplace par son contraire, et l'axiomatique dans sa forme actuelle se trouve profondement modifiée. Et cela change complètement les mathématiques et les sciences.

Les mathématiques actuelles gardent leur pluriel parce que la tentative de les unifier dans une seule théorie axiomatique des ensembles n'a pas abouti. Toutefois, la théorie de référence actuelle (celle de Zermelo-Fraenkel), constitue une avancée considérable dans cette voie d'unification, en ce que la quasi-totalité des concepts mathématiques actuels peuvent être définis dans cette théorie, et obéissent aux mêmes axiomes fondamentaux, qui sont ceux de cette théorie. Grâce à cela, on voit beaucoup plus clair dans la forêt des mathématiques, et de nombreux domaines jadis séparés et ayant leur propres langages, outils et méthodes, se sont unifiés pour devenir de vrais arbres. Mais dans le même temps ces arbres se sont condérablement ramifiés pour engendrer d'innombrables sous-domaines, ce qui rend l'ensemble de nouveau très touffu.

S'il y a ou presque une unification des mathématiques grâce à la notion d'ensemble, c'est très loin d'être le cas le cas pour l'ensemble des sciences, et à plus forte raison pour l'ensemble des connaissances, la philosophie, la théologie, la religion et Dieu compris ! L'Arbre nommé LA Science dont toute science ou toute connaissance serait une simple branche est-il un condamné à n'être qu'un Saint-Graal, une entreprise irréalisable ? La clef d'une telle science existe-t-elle ?

La réponse à cette question est fort simple : une telle science était impossible tant que le moteur du raisonnement était le principe de non-contradiction. Une fois cet obstacle levé, alors apparaît une remarquable propriété de la nouvelle science apparaît, comme celle d'un arbre.

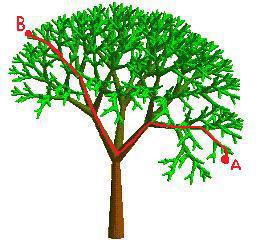
Observez attentivement un arbre et vous découvrirez une de ses propriétés, aussi simple que remarquable : en l'abordant par nimporte laquelle de ses branches et même par n'importe quelle feuille, vous pouvez, en naviguant dans l'arbre, atteindre n'importe quelle autre branche ou feuille, sans avoir besoin de sauter de branche en branche ou de feuille en feuille. L'arbre a sa racine d'où part son tronc, qui se divise en plusieurs branches qui se divisent à leur tour, etc. Chaque branche a sa propre racine, qui est le point où elle rejoint une branche plus grosse. Une propriété importante de l'arbre est que toute branche de l'arbre est à son tour un arbre (un sous-arbre) dans l'arbre, qui reproduit à son niveau le même modèle que l'arbre tout entier.

C'est ici la clef de l'affaire, qui permet d'un point A de l'arbre d'atteindre tout autre de ses points B, en toute continuité, en naviguant de branche en branche. Il suffit de suivre l'algorithme suivant : De A, on suit la branche jusqu'à sa racine. Puis on suit le parcours vers le tronc commun avec le point de destination B. Ce tronc commun est par définition la toute première grosse branche qui porte à la fois A et B. Il en existe, et à défaut ce tronc commun est tout simplement le tronc de l'arbre entier. Celui-ci est la solution par défaut pour le parcours, au cas où l'on ne trouve pas de parcours plus économique. Puis du tronc commun, on se dirige vers la racine de la plus grosse branche qui porte le point de destination B. Les racines sont de plus en plus petites en allant vers B. A chaque jonction, il existe toujours une branche qui est le bon itinéraire parmi deux ou plusieurs possibles. Si on s'égare et l'on prend une mauvaise branche, il suffit de revenir en arrière, en recherchant de nouveau un tronc commun. Et on finit toujours par atteindre B.

L'abandon du principe de non-contradiction signifie l'adoption de son contraire, qui peut se formuler en ces termes : "Le contraire de toute vérité est toujours une autre vérité". C'est ce que j'appelle le principe d'alternation (voir La fin de la science aristotélienne et Le Théorème pour public initié). Le principe d'alternation instaure un nouveau paradigme scientifique où tout devient maintenant possible, parce que justement "Le contraire de toute vérité est toujours une autre vérité". Cela rend désuette du même coup la méthodologie axiomatique, car l'un des points clefs de cette méthode est la recherche de l'ensemble des théorèmes que l'on peut déduire à partir d'un système d'axiomes, et leur séparation des non-théorèmes. C'est du souci de la séparation entre théorèmes et non-théorèmes que l'abadon du principe de non-contradiction (donc le principe d'alternation) libère maintenant. Comme le montre l'arbre, d'un point A on peut atteindre n'importe quel autre point B. Il y correspond le fait que du point de départ d'un raisonnement, on peut maintenant atteindre n'importe quelle conclusion. Ceci était une horreur pour le logicien, à savoir de se trouver dans une situation où il peut démontrer tout et n'importe quoi, et surtout tout et son contraire ! Le principe de non-contradiction est donc une règle interdisant d'aboutir comme conclusion à tout et à son contraire. C'est ce que l'on conçoit comme étant une catastrophe logique !

Mais en quoi c'est une catastrophe de dire ceci : "D'un point A, je peux me rendre à tout autre point B que je souhaite" ? En quoi c'est un malheur pour un français par exemple de dire : "De tout coin A de France, il existe toujours une route me permettant d'aller à tout autre point B de France" ? Ceci place simplement dans une toute autre logique où la notion de démonstration et le but de la démonstration change complètement. Puisqu'on peut désormais tout démontrer à partir de tout, le but de la démonstration n'est donc plus de savoir où on peut aboutir (théorème), où on ne peut pas aboutir (non-théorème), et où on ne peut ni l'un ni l'autre (énoncé indécidable). Mais le but d'une démonstration est simplement (comme dans l'arbre) de trouver un intinéraire sans tromper pour aller où l'on souhaite. Et si on se trompe à un croisement, la situation n 'est pas aussi dramatique qu'avec le principe de non-contradiction. On peut toujours revenir sur ses pas et chercher le bon intinéraire. Et cet itinéraire rallongé qu'on a emprunté suite à l'erreur (notion qui est désormais faible et relative) est dans l'absolu simplement un autre itinéraire pour atteindre la même destination. Si je pars par exemple de Clermont-Ferrand pour aller à Paris au nord, je peux y aller par voie directe, ou faire un détour par Marseille au sud ! Ce n'est pas le bon itinéraire en ce sens simplement que ce n'est pas le plus court. Mais si cet intinéraire correspond à une volonté (car après tout je peux avoir une raison de passer exprès par Marseille...), alors c'est aussi un bon itinéraire.

Contrairement donc à ce qu'on a toujours cru et redouté, l'abandon du principe de non-contradiction ne signifie pas un chaos logique. Si chaos il y a, il ressemble exactement à l'arbre et au dédale de ses branches. Il s'agit plutôt d'un chaos bien organisé, ayant de splendides propriétés, une logique splendide que j'appelle la Logique de l'Arbre, mais aussi Logique de Cycle, ou encore Logique d'Alter ou Logique alternative (par analogique au courant alternatif). Cette dernière appellation est par opposition à Logique continue (par analogique au courant continu), qui elle correspond au paradigme du principe de non-contradiction. La hantise d'un mathématicien est d'avoir à écrire que 0 = 1 est une vérité mathématique, car cette égalité est une des manières de définir le paradoxe ou contradiction, ce qu'interdit le principe de non-contradiction. Mais cette égalité est la définition du Cycle 1 dans la nouvelle logique, et plus généralement le Cycle X est défini par l'égalité : 0 = X (voir la vidéo L'algèbre du Cycle).

Puisqu'avec l'abandon du principe de non-contradiction on peut désormais démontrer toute chose B à partir de toute chose A, tout devient donc un théorème. Pour cela, la nouvelle méthodologie est appelée théorématique, par opposition donc à axiomatique. L'activité théorématique consiste à organiser les notions selon la Logique de l'Arbre ou Logique de Cycle.

C'est tout l'enjeu et de toute la raison d'être de la Science Nouvelle et de son paradigme. Ce paradigme permet enfin de faire la lumière sur tout, d'aller loin, très loin dans la connaissance de la vérité.

Le nouveau paradigme n'exclut pas l'actuel mais l'inclut, exactement comme si on passe de la science de la "pomme" à la science des "fruits" en général. Le paradigme qui limite aux pommes ne permet pas de parler des poires, des abricots, les cérises, et des fruits exotiques comme la banane, la mangue, la goyave ou le kiwi. Actuellement, c'est comme si tout ce qui traite d'autre chose que des pommes n'est pas de la science. C'est ainsi par exemple que, actuellement, tout ce qui concerne Dieu n'est pas de la science, jusqu'à preuve du contraire.

Mais désormais, toute question, toute chose, a sa place dans la Science Nouvelle. Toute notion, quelle qu'elle soit, peut servir de notion d'entrée (ou objet) de la nouvelle science. Par exemple, la science des pommes (appellons la par exemple la "pommologie"), pourvu qu'elle soit poussée suffisamment loin, peut amener à traiter des ensembles (objet des mathématiques), de la matière (objet de la psysique), du vivant (objet de la biologie), de l'information (objet de l'informatique), etc. Et de la même façon, tout autre objet conduira tôt ou tard à la pommologie. On a donc la seule et même science avec le nouveau paradigme, le reste est une simple question de l'angle sous lequel cette seule et même science est abordée. C'est cet angle qui donne son nom à la science.

La seule différence est que selon la notion d'entreé, la chemin peut être plus ou moins long pour atteindre un autre sujet. En abordant par exemple la science par la notion de pomme, le chemin sera court pour en arriver à la poire ou au kiwi, mais long pour aboutir au théorème de Pythogore, aux trous noirs ou aux quasars. Et inversement, en commençant par ceux-ci, la route sera longue pour en arriver à la science des pommes et aux recettes pour faire de bonnes compotes. Mais désormais cette passerelle existe; en partant de tout sujet, on aboutit toujours à tout autre sujet.

Ainsi, la forêt des sciences et des connaissances devient un seul Arbre de la Science. Le reste est une simple question de savoir par quelle branche (ou notion d'entrée ou objet) on aborde ce seul Arbre. Et selon la notion d'entreé, la chemin peut être plus ou moins long pour atteindre un autre sujet (une autre branche). Mais on peut simplement aborder l'Arbre par les racines. Cela signifie alors que la notion d'entrée est une notion fondamentale. C'est ce que sont les notions comme celle de nombre, d'ensemble, de chose ou d'existence (voir Chose, Existence, Ensemble).

Voir aussi :
L'Univers fractal, l'Univers-Dieu
Le secret pour faire la Science du Tout