Le problème de l'Egalité
ou Le problème de l'Ontologie

Si les rélations de la forme X = Y sont appelée "Egalité",
alors il faut réserver par exemple le terme "Identité" pour désigner les cas particuliers de la forme "X = X".
Mais si on appelle "Egalité" le cas particulier "X = X",
alors il faut appaler par exemple "Equivalence"le cas général de la forme "X = Y".
Mais quelle que soit la terminologie adoptée,
c'est ce cas général qui soit être la relation scientifique notée par le signe "=" et qui sert à exprimer les équations.

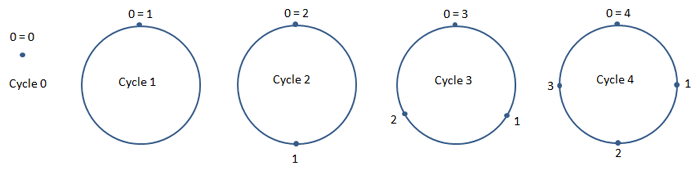
Les égalités de la forme 0 = 0, 1 = 1, 2 = 2, X = X, etc., sont celles du Cycle 0;
la science actuelle fonctionne seulement avec ce type d'égalité,
mais elle n'est seulement qu'un cas très particulier dans l'infinité de types d'égalité qui existent dans l'Univers TOTAL.
Les égalités de type : 0 = 1 ou 1 = 0, 1 = 2 ou 2 = 1, 72 = 73 ou 73 = 72, X = X + 1 ou X + 1 = X, etc.,
sont celles du Cycle 1, et avec ce type d'égalité de la forme générale X = Y commence
la "Terra Incognita" ("Terre Inconnue") ou "Universum Incognita" ("Univers Inconnu") pour la science actuelle,
toute l'immensité actuellement inconnue de l'Univers TOTAL, que le Fils de l'homme révèle aujourd'hui...
Le paradigme du Cycle, c'est le paradigme de l'Equivalence.

L'Equivalence, la notion d'Egalité de la Science Nouvelle
--> Que faut-il entendre par "MEME chose" ?
--> Le problème de l'Egalité, c'est le problème de la Négation
--> L'Equivalence est la bonne conceptionn de l'Egalité

Langage universel des ensembles et Equivalence universelle
--> L'Equivalence et la physique
--> Ensembles et classes d'Equivalence

Documents associés :
Problème de l'Infini
Loi de l'Alpha et de l'Oméga
Algèbre universelle des ensembles
Théorie de l'Universalité

L'Equivalence, la notion d'Egalité de la Science Nouvelle

Que faut-il entendre par "MEME chose" ?

Le problème de l'Egalité, c'est le problème des énoncés suivants : "A est B","A est un B" (problème de l'appartenance), "A et B sont la MEME chose"(problème de l'identité ou problème du mot MEME), etc. C'est le problème du verbe ETRE (problème ontologique).

Par exemple, ce principe formulé par Aristote pose un problème d'ontologie : « Il est impossible qu’un même attribut appartienne et n’appartienne pasen même temps et sous le même rapport à une même chose» (Aristote, Métaphysique, 1005 b 19-20).

Tout d'abord problème est caché dans le mot "attribut" ("posséder un attribut ou ne pas le posséder", c'est "être ou ne pas être"). Et ensuite le problème est caché dans le mot "MEME" qui joue un rôle crucial dans cet énoncé : "même attribut", "même temps", "même rapport", "même chose".

A ce propos, est-ce que "4 + 6" et "2 x 5" sont la "même chose" ? On répondra évidemment que oui, parce que les deux sont deux manières différentes de dire 10. C'est ce 10 qui leur est commune qui fait dire que c'est la même chose, et on écrit l'égalité : 4 + 6 = 2 x 5.

Mais il n'empêche qu'il s'agit bel et bien de deux manières différentes, de deux opérations différentes, d'une part une addition et d'autre part une multiplication. Par "c'est la même chose" on veut dire que ces deux opérations différentes donnent le même résultat. C'est comme le fait de dire que Théophile et Angélique ont le même âge, à savoir 10 ans par exemple. Mais Théophile et Angélique ne sont pas la même chose à proprement parler, car l'un est garçon par exemple et l'autre est une fille, exactement comme 4 + 6 est une addition et 2 x 5 est une multiplication. Les deux donnent comme résultat 10, qui est ici un attribut commun, une propriété commune à ces deux opérations différentes. Si on écrit l'égalité 4 + 6 = 2 x 5 à cause de l'attribut qu'elles ont en commun, à savoir le résultat, alors on doit aussi écrire Théophile = Angélique à cause de l'attribut qu'ils ont eux aussi en commun, à savoir l'âge !

C'est la même question qui se pose au sujet de deux feuilles identiques A et B sorties d'une même rame. Elles sont deux objets physiques différents, mais elles ont un certain nombre d'attributs communs : même forme rectangulaire, mêmes dimensions (par exemple le format A4), même densité (donc même masse), etc. C'est pourquoi très naturellement on dira que A et B sont la "même chose". Et pourtant A et B ne sont pas la même chose. Et pourtant aussi c'est la "même chose"... C'est toute la subtilité du problème de l'égalité, du problème des attributs, du problème de l'ontologie, le problème de l'ETRE ou du verbe ETRE.

Le problème de l'Egalité, c'est le problème de la Négation

Le problème de l'égalité (ou de l'ontologie) est étroitement lié au problème de la Négation. Car les phrases par exemple : "Dieu n'est pas une chose qui existe", "Jésus n'est pas le Fils de Dieu", "Jésus n'est pas Dieu", "Hubertelie n'est pas Jésus", etc., sont des problèmes de négation, mais aussi des problèmes d'ontologie (des problèmes de l'ETRE) justement pour cette raison-là ! C'est la négation qui introduit le problème, car là où on ne nie pas, on ne dit pas non plus "A n'est pas B" ou "A n'est pas un B".

La science qui ne fonctionne plus avec la négation, c'est la science aussi où le problème de l'égalité (ou de l'ontologie) est résolu, car son égalité (ou son ontologie) est celle de l'équivalence, un point c'est tout. Et une science qui repose sur l'Univers TOTAL (l'Ensemble de toutes les choses) ne fonctionne plus avec la négation mais avec l'alternation. Son ontologie est celle de l'Univers TOTAL, à savoir l'équivalence donc. Deux chose A et B, si différentes soient-elles, sont toujours égales d'un certain point de vue, car elles ont toujours un certain attribut commun (à défaut l'attribut commun d'être une chose), elles appartiennent toutes les deux à l'Univers TOTAL, qui est leur trait d'union. Elles appartiennent au même Univers TOTAL, elles ont le même Univers TOTAL, qui est le même attribut suprême qu'elles possèdent. Du point de vue cet Univers, elles sont donc égales.

L'Equivalence est la bonne conception de l'Egalité

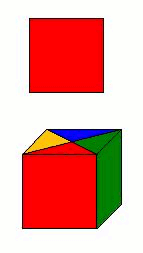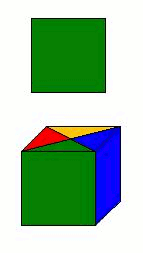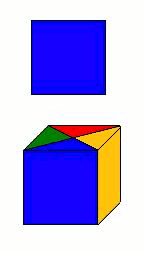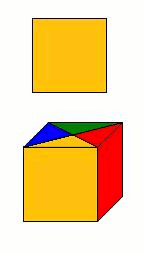
Voici ci-dessus quatre choses (quatre cubes) que l'on peut appeler A, B, C, D. Ces choses sont différentes d'abord tout simplement parce qu'elles sont PHYSIQUEMENT différentes, c'est-à-dire qu'elles sont quatre objets physiques bien distincts. Et ensuite elles sont différentes parce qu'elles ne sont pas physiquement orientées de la même façon, elles ne nous présentent pas la même face, mais quatre faces de couleurs différentes. Vus sous cet angle, ces quatre cubes sont quatre carrés différents, de couleur différents. Ces quatre cubes peuvent représenter par exemple quatre électrons dans quatre états quantiques différents, qui n'ont donc pas les mêmes nombres quantiques, donc qui ne vont pas réagir physiquement de la même manière, quand ils sont soumis à une certaine même action. Et pourtant ces choses sont la seule et même chose, qui tourne.

Les quatres choses ne sont donc pas égales au sens strict de l'identité, elles ne sont pas la "même chose" de ce point de vue. Mais elles sont égales au sens de l'équivalence (ce qui est de loin le plus important), elles sont la "même chose" de ce point de vue.

L'égalité stricte, celle avec laquelle la science fonctionne actuelle, consiste à dire seulement A = A. Cette égalité se réduit donc à l'identité. Une science qui ne fonctionne qu'avec cette égalité est normalement stérile, c'est ce que j'appelle la science du cycle 0 (voir la Loi de l'Alpha et de l'Oméga). La notion de cycle est très étroitement associée à la relation d'équivalence. D'une manière très générale, un cycle s'écrit : A = B, où A et B sont deux nombres quelconques (dans la Théorie universelle des ensembles, toute chose est un ensemble et tout ensemble est un nombre). A = B est très précisément l'expression du cycle (B - A), qui s'écrit aussi : 0 = B - A. En particulier donc, si A et B sont le même nombre (au sens de l'identité, c'est-à-dire A = A), alors il s'agit du cycle (A - A), donc du cycle 0, qui est donc l'égalité de la forme : 0 = 0. Par contre l'égalité 3 = 7 par exemple définit le cycle (7 - 3) ou cycle 4, dont l'expression canonique est : 0 = 4.

La science qui fonctionne donc avec la seule égalité A = A est aussi pauvre que de faire la science avec comme seul nombre 0 ! Si la science actuelle n'est pas complètement stérile (ce qu'elle aurait dû être), c'est heureusement parce qu'elle ne fonctionne pas vraiement avec cette égalité, mais implicitement et clandestinement avec une certaine dose d'équivalence, donc de cycle autre que 0, qu'elle n'avoue pas comme tel. C'est ce qui fait qu'elle peut écrire des choses comme 4 + 6 = 2 x 5, ce qu'elle n'a normalement pas le doit d'écrire, si elle s'en tenait vraiment à cette égalité de la forme A = A.

En effet, avec cette égalité, on n'a le droit que de dire : 4 + 6 = 4 + 6, 2 x 5 = 2 x 5, 10 = 10, etc., bref A = A. On doit donc rigoureusement avoir la MEME chose de part et d'autre du signe "=", pour que ce soit cette égalité stricte de type A = A (ou cycle 0) et non pas l'équivalence. Ainsi, Einstein par exemple n'avait pas le doit d'écrire E = mc², car on n'a pas rigoureusement la MEME chose de part et d'autre du signe de l'égalité. Einstein aurait dû seulement dire : E = E, mc² = mc², c'est tout ! Aucune opération n'est possible avec cette égalité, ni en mathématique, ni en physique, ni partout ailleurs. Avec cette égalité donc, il n'y a tout simplement plus de science, la science avec cette égalité tautologique est plus que stérile, elle est carrément morte !

C'est donc parce que l'on fonctionne avec une certaine dose d'équivalence ou de cycle non nul (sans le dire) que la science a été possible, et que l'on a pu commencer à dire des choses du genre : 1 + 1 = 2. Le signe "=" qui apparaît dans cette écriture est en fait une équivalence. Une équivalence entre deux choses différentes. La première est une opération, celle qui consiste à ajouter 1 à 1. Et la seconde est tout simplement le nombre 2. Cette égalité signifie que ces deux choses, bien que différentes, sont la même chose.

La puissance de l'équivalence est bridée quand la science ne repose pas sur l'Univers TOTAL. Mais c'est avec l'Univers TOTAL que l'équivalence acquiert sa puissance maximale, elle est alors l'équivalence universelle, que j'appelle l'Universalité, un concept infiniment plus fort que la Relativité. L'Universalité dit que deux choses quelconques X et Y, si défférentes soient-elles, sont équivalentes : X = Y (voir la Théorie de l'Universalité).

Langage universel des ensembles et Equivalence universelle

L'Equivalence et la physique

La notion de relation (ou de lien) est fondamentale en science, tant et si bien qu'on peut définir l'activité scientifique comme étant l'activité qui consiste à exprimer les relations entre les choses, à établir les liens entre elles. Par exemple, l'écriture E = mc² (la très célèbre formule de la relativité d'Einstein) établit une relation entre l'energie (ici E), la masse (ici m), et la vitesse de la lumière (ici c). Elle est fondamentalement une égalité entre deux énergies, E et mc².

La même vérité scientifique peut être exprimée en termes d'équivalence entre l'énergie E et la masse m. Cela signifie qu'on parle alors d'une égalité entre E et m, au carré de la vitesse de la lumière près, c'est-à-dire à la constante c² près. Autrement dit, cette égalité entre E et m est nuancée ou modérée par c². On dira aussi que "E et m sont égaux modulo c² ".

La même vérité scientifique peut être exprimée en terme d'appartenance à une certaine classe de choses c'est-à-dire simplement à un certain ensemble de choses, ici la classe de l'énergie ou la classe de la masse. Deux éléments A et B de cette classe sont soit égaux (c'est le cas s'ils sont deux énergies ou deux masses), soit l'un des deux est obtenu en multipliant ou en divisant l'autre par c² ou par une quantité qui est le carré d'une vitesse.

Cet exemple bien connu montre qu'une même vérité scientifique, E = mc², peut s'exprimer aussi bien comme une égalité, comme une équivalence, ou comme une appartenance à une certaine classe de choses ou ensemble. Toutes les relations se ramènent fondamentalement à trois relations : l'égalité, l'équivalence et l'appartenance, qui sont en fait comme les trois mots chose, existence et ensemble; c'est-à-dire simplement trois façons différentes de parler d'une seule et même chose, à savoir le verbe ETRE.

Ensembles et classes d'Equivalence

Le verbe ETRE est fondamental dans la Science Nouvelle, tout simplement parce que c'est le verbe de l'égalité ou de l'identité, relation très fondamentale en science. Comme par exemple dans la célèbre formule de la Relativité d'Einstein : E = mc². On ne voit pas comment on pourrait faire la science si on ne peut pas dire des choses du genre : A = B.

Une science qui conçoit bien la notion d'ETRE (donc une science dont l'ontologie est bonne) ne sépare pas les mots ou les notions qui sont des formes différentes de la seule relation d'égalité ou d'identité, c'est-à-dire simplement des manières différentes d'employer le seul et même verbe ETRE, ou la seule et même notion d'ETRE en tant que nom, comme par exemple quand on dit "être humain". Une très importante autre manière de parler de la seule et même égalité ou identité, est la relation d'équivalence, très importante en mathématiques, mais aussi en physique (bien que les physiciens ne donnent pas à ce mot tout à fait le même sens qu'en mathématique), comme par exemple quand on parle d'équivalence masse-énergie, qui exprimée par fameuse égalité : E = mc². Il s'agit ici de l'égalité entre deux énergies (E d'une part et mc² d'autre part), mais qui est aussi quelque part une égalité entre l'énergie (E donc) et la masse (ici m), à une constante près, qui est ici la vitesse de la lumière c (et plus exactement ici son carré). C'est cette égalité indirecte (ou au sens très large) que les physiciens appellent une équivalence.

Mais au sens le plus général (donc applicable en mathématique, en physique ou dans tout autre autre domaine), on parle d'équivalence entre deux choses A et B, quand ces deux choses sont égales d'un certain point de vue donné P. On dit alors dans le jargon que "A et B sont égaux modulo P". En règle très générale, P traduit une certaine propriété commune à A et B, une appartenance commune à un certain ensemble C décrit par la propriété P, c'est-à-dire dont les éléments sont les choses qui vérifient cette propriété P. Cet ensemble C est alors appelé la "classe d'équivalence" commune à A et B. Cela veut dire simplement que vues dans cet ensemble C (donc au regard de la propriété P commune aux éléments de cet ensemble C), A et B sont une même chose, ils sont identiques, l'un peut parfaitement remplacer l'autre et vice-versa, si on ne s'intéresse qu'à la propriété commune P que ces choses ont. Sinon, si donc on s'intéresse à une autre propriété Q qu'une des choses posséderait et pas l'autre, alors elles se différencient par cette propriété Q, elles ne sont plus équivalentes (ou égales) du point de vue de cette autre propriété.

Par exemple, si je demande un fruit sans autre précision, on peut me donner indifféremment une pomme, une banane, un abricot ou un kiwi. Au regard de la propriété P exigée, celle de fruit, ces choses sont équivalentes (elles sont donc "égales modulo fruit" comme on dirait dans le jargon); elles appartiennent à la classe des fruits, qui est leur classe d'équivalence, leur ensemble commun tout simplement. Mais si je demande une pomme, on ne peut plus me donner une banane par exemple, car les deux choses n'appartiennent plus à la même classe (ou ensemble), ici la classe des pommes, qui est dans cet exemple une sous-classe de la classe des fruits. Mais on peut indiféremment me donner une pomme golden, une pomme red-chief, une pomme canada, une pomme fuji, une pomme royal gala, etc. Au regard de la nouvelle propriété Q exigée, celle de pomme, ces choses sont équivalentes (ou égales), mais au regard de cette propriété, une pomme golden par exemple n'est plus équivalente à une banane.

Ce que je viens d'expliquer est tout simplement la conception la plus naturelle et universelle de la notion d'ensemble, celle de la Théorie universelle des ensembles. Un ensemble est simplement la donnée d'une propriété donnée, qui caractérise ses éléments. Et en règle très générale, cette propriété est désignée tout simplement un mot ou un nom (comme par exemple fruit ou pomme) qui est alors le nom commun des éléments de l'ensemble. C'est ainsi que cette très importante notion est utilisée dans le langage courant et dans le raisonnement naturel.

Le nom commun (ou mot commun) le plus important dans la Science Nouvelle est le mot chose (voir Chose, Existence, Ensemble). C'est la propriété la plus commune, celle que possède, eh ben, toutes les choses ! Elle définit une classe d'équivalence ou un ensemble, qui est le plus vaste qui soit, ensemble dans lequel se déroule toute la Science Nouvelle. Cet ensemble est tout simplement l'Univers TOTAL, par définition l'Ensemble de toutes les choses. Au regard de la propriété commune de chose, deux choses A et B sont équivalentes, et on écrit : A = B modulo chose ou modulo Univers. Cette équivalence (ou égalité) fondamentale entre les choses, est tout simplement la relation appelé dans le langage courant le verbe ETRE. Au regard du mot chose ou de la classe d'équivalence ou ensemble Univers, pour deux choses absoluments quelconques A et B, on a A = B, c'est-à-dire la phrase "A EST B" est vraie.