De l'axiomatique à la théorématique
Les axiomes de
ZFC
Rappelons la liste
des axiomes de ZF :
A0- Axiome de l'ensemble vide :
" Il existe un ensemble n'ayant aucun ensemble comme élément"

A1- Axiome
de l'extensionnalité :
"
Deux ensembles ayant les mêmes éléments
sont égaux"
A2- Axiome de la paire :
"
Pour deux ensembles a et b, il existe un ensemble c dont
les éléments
sont a et b"
En fait, cet axiome est un théorème, il se déduit
de l'axiome de l'ensemble vide et de l'axiome de l'ensemble
des parties d'un ensemble.
A3- Axiome de l'ensemble des parties d'un ensemble :
"
Pour tout ensemble a, il existe un ensemble b dont les éléments
sont les parties de a"
(Un
ensemble a est une partie d'un ensemble b, ou est inclus
dans b, si tous
les éléments de a sont aussi des éléments
de b.)
A4- Axiome
de la réunion :
"
Pour tout ensemble a, il existe un ensemble b dont les éléments
sont les éléments des éléments
de a".
A5- Schéma
de remplacement :
"
Pour tout ensemble a et pour toute relation fonctionnelle
f, il existe un ensemble b dont les éléments sont
les images des éléments de a par f ".
(Une relation,
notée
R (x, y), est un énoncé portant sur deux variable
x et y. Par exemple les énoncés "x appartient à y", "x
= y", "Il
existe un ensemble ayant x et y pour élément",
etc., sont des relations. Cette relation R(x, y) est fonctionnelle
si
pour tous x, y et y', R(x, y) ET R(x, y') => y = y'. Autrement
dit, une telle relation est une correspondance; à un
x donné,
il lui correspond aucun y ou un seul y, mais pas plus d'un.
Dans les trois exemples précédents, seule la deuxième relation
est fonctionnelle, car : x = y ET x = y' => y = y'. Une
relation fonctionnelle est le plus souvent
notée : y = F(x), et
y est appelé l'image
de x par cette relation fonctionnelle.
Bref une relation fonctionnelle est ce qu'on appelle communément
une "fonction", mais dans son sens le plus général,
pas seulement dans le cadre de nombres.)
A6- Axiome de l'infini :
" Il existe un ensemble inductif"
(Un ensemble a est
inductif si l'ensemble vide est un de ses éléments, et si
pour tout élément x lui appartenant, l'ensemble:
x U {x} est aussi un de ses éléments.)
Ce sont les axiomes de base de ZF, auxquels on ajoute souvent
l'axiome A7 suivant :
A7- Axiome de fondation :
"
Pour tout ensemble non vide a, il existe un élément
b de a tel que a et b soient disjoints"
(Deux ensembles
sont disjoints s'ils n'ont aucun élément commun)
ZFC est la théorie avec l'axiome du choix, qui est
l'énoncé suivant :
A8-Axiome du choix :
" Pour tout ensemble a non vide dont les éléments
sont deux à deux disjoints, il existe un ensemble b
ayant un élément et un seul dans chaque élément
de a".
Voilà pour
la théorie axiomatique standard, et c'est ici que
commencent les problèmes que je soulève, et
qui nécessitent une autre approche de la théorie des ensembles,
donc qui donnent sa raison d'être à la Théorie
des univers.
Le
problème de l'ensemble plein

Vidéos : 1) La
science exacte qui ment 2) Toute la lumière sur
les Paradoxes
L'ensemble
vide sans l'ensemble plein
Avec ce système
d'axiomes, il existe au moins un ensemble vide (axiome
A0), et même on démontre avec A1 que cet ensemble vide est unique,
et on le note 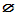 .
C'est "L'ensemble n'ayant aucun ensemble
comme élément", y compris donc aussi lui-même, qui n'est pas
son propre élément.
.
C'est "L'ensemble n'ayant aucun ensemble
comme élément", y compris donc aussi lui-même, qui n'est pas
son propre élément.
Toutes
les faiblesses (ou même simplement toutes les graves lacunes)
de ZF et de toutes
les théories axiomatiques classiques des ensembles se résument
à une seule : elles parlent de l'ensemble vide sans
l'ensemble
plein ou ensemble
de tous les ensembles.
Voici ce que
devrait être l'énoncé de l'axiome de l'ensemble plein :
A'
6 : Axiome de l'ensemble plein :
" Il existe un ensemble ayant tout ensemble comme élément"
ou :
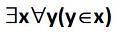
Non seulement
cet axiome manque, mais on ne peut le déduire comme
théorème
du système d'axiomes choisi. Et
ce système d'axiomes est justement élaboré de
telle sorte qu'il rende impossible l'existence
de l'ensemble plein et d'autres, qualifiés de "pathologiques",
parce qu'ils causent des paradoxes au sens le plus négatif
du terme, c'est-à-dire des contradictions.
C'est le principe
de non-contradiction, très fondamental dans la pensée
scientifique actuelle, qui interdit l'existence d'ensembles possédant
les propriétés de l'ensemble plein et d'autres,
propriétés qualifiées
de contradictoires.
Le
Paradoxe de Russell
Parmi
les plus représentatifs du problème des ensembles,
il y a deux paradoxes : la Paradoxe
de Russell* et le Paradoxe
de Burali-Forti*. Avoir résolu
ces deux paradoxes (voir aussi la vidéo Toute
la lumière sur le Paradoxes) et même un seul des
deux, c'est avoir résolu du même coup tous les
paradoxes, car tous ont en fait la seule et même cause. Ce
ne sont pas toutes celles
qu'on a imaginées (entre autres le "pauvre et innocent" ensemble
plein chéri...), mais une qu'on ne soupçonne jamais,
le vrai Diable de l'affaire
: Le
problème
de la Négation !
En
effet, effet, sans la négation,
le connecteur NON, on ne pourrait faire
la négation d'une chose donnée,
et donc se trouver devant une chose vraie en même temps
que sa négation, c'est-à-dire
devant des situations du genre : "V ET non-V"
ou encore "V
<=> non-V" (ou V est
un énoncé quelconque), ce
qu'on appelle un "paradoxe",
à comprendre "contradiction"
:

Le schéma de paradoxe de type Russell ou Burali-Forti;
et même simplement de type "Paradoxe du Menteur'
:
Vrai <=> Faux.
Le
paradoxe de Russell concerne l'ensemble A dont
les éléments sont exactement les ensembles
(appelons-les les ensembles
alpha ou 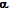 )
qui n'appartiennent pas à eux-mêmes : NON
(
)
qui n'appartiennent pas à eux-mêmes : NON
(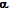

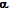 ) ou
:
) ou
: 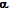

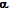 .
La question est de savoir si A appartient
à lui-même. Autrement dit, est-il oui ou non un ensemble alpha (
.
La question est de savoir si A appartient
à lui-même. Autrement dit, est-il oui ou non un ensemble alpha (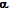 ).
Si oui, alors il n'appartient pas à lui-même, puisque c'est
la propriété caractéristique des alpha.
Mais s'il n'appartient pas à lui-même, alors il possède justement
la propriété des alpha, donc
il appartient à lui-même, puisque justement il est par définition
l'ensemble des alpha; d'où
le "paradoxe" de Russell. Ce paradoxe implique immédiatement
que l'ensemble plein (ou ensemble
de tous les ensembles) ne peut pas exister. En effet,
l'axiome A5 (et plus particulièrement une de ses conséquences
nommée le schéma de compréhension) dit que si on a un ensemble E donné,
ses éléments x vérifiant
une certaine propriété P(x) donnée
constituent un ensemble E', qui est donc
un sous-ensemble (ou partie) de E. Par conséquent,
si l'ensemble plein existe (appelons-le
Oméga ou
).
Si oui, alors il n'appartient pas à lui-même, puisque c'est
la propriété caractéristique des alpha.
Mais s'il n'appartient pas à lui-même, alors il possède justement
la propriété des alpha, donc
il appartient à lui-même, puisque justement il est par définition
l'ensemble des alpha; d'où
le "paradoxe" de Russell. Ce paradoxe implique immédiatement
que l'ensemble plein (ou ensemble
de tous les ensembles) ne peut pas exister. En effet,
l'axiome A5 (et plus particulièrement une de ses conséquences
nommée le schéma de compréhension) dit que si on a un ensemble E donné,
ses éléments x vérifiant
une certaine propriété P(x) donnée
constituent un ensemble E', qui est donc
un sous-ensemble (ou partie) de E. Par conséquent,
si l'ensemble plein existe (appelons-le
Oméga ou 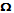 ), alors ses éléments alpha (
), alors ses éléments alpha (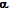 )
qui vérifient la propriété de ne
pas appartenir à eux-mêmes (la non-auto-appartenance) P(
)
qui vérifient la propriété de ne
pas appartenir à eux-mêmes (la non-auto-appartenance) P(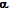 ) :
) : 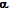

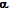 ,
forment un ensemble A; chose qu'interdit
le "paradoxe" de Russell.
,
forment un ensemble A; chose qu'interdit
le "paradoxe" de Russell.
Le
paradoxe de Russell est commun comme un paradoxe de la théorie
des ensembles. On le qualifie souvent de paradoxe d'"auto-référence",
parce qu'une certaine notion fait référence à elle-même, comme
la notion d'ensemble (pour
l'ensemble de tous les ensembles), ou comme
le fait d'être un ensemble qui "n'appartient
pas à lui-même". Mais il s'agit d'un
mauvais diagnostic, car l'auto-référence n'est pas un problème
en soi. Les notions de récurrence ou
de récursivité par exemple,
sont des situations d'auto-référence qui ne posent aucun problème.
Mais c'est quand la négation se mêle de cette auto-réfence
que l'affaire se complique
Le
Paradoxe de Russell est simplement un
paradoxe de logique pure, qui porte sur les notions comme la
"relation
binaire",
le quantificateur universel "TOUT",
et surtout sur le connecteur
de négation NON. Et à ce titre, il est simplement
comme le
Paradoxe du Menteur, de la forme : Vrai <=> Faux ou
: Vrai
<=> NON Vrai. Tout est là.
Russell
a d'ailleurs popularisé ce problème sous le nom
du "paradoxe
du barbier" : "Le barbier d'un village rase tous les
hommes du village qui ne
se rase pas eux-mêmes. Le barbier
se rase-t-il
lui-même ?" Et d'une manière générale, posons-nous le problème suivant
concernant une relation binaire R et une chose
A : "Une chose A entretient
la relation
R avec toute chose
n'entretenant pas cette relation avec elle-même. Est-ce
que la chose A entretient cette relation R avec
elle-même ?"
Le
problème s'écrit simplement ainsi : "Pour tout x, x
R A <=> NON (x R x); A R A ? " Et alors pour
A la réponse est : A R A <=> NON
(A R A).
Et
c'est principalement un problème de négation;
la dite auto-référence n'y est pour rien, ni le quantificateur
TOUT ou la relation R. On
se moque même de savoir si on est dans les ensembles, dans
les collections, dans les classes,
ou dans un village avec un barbier. On se moque aussi de savoir
s'il s'agit de la relation d'appartenance ou le fait de se
raser. Tans
qu'il n'y a pas la moindre goutte de négation dans
l'affaire, le problème ne se pose pas. La
preuve : posons le problème sans la négation : "Une
chose A entretient
la relation R avec toute chose
entretenant cette relation avec elle-même.
Est-ce que la chose A entretient
cette relation R avec
elle-même ?" Le problème est entièrement posé
affirmativement, et il s'écrit :
"Pour tout x, x
R A <=> x R x; A R A ? " Et alors
pour A la réponse est : A R
A <=> A R A.
On
a donc beau tourner la chose comme on veut, il n'y a aucun
problème ! Et pourtant il y a tous les autres ingrédiens :
le même contexte, le mot TOUT,
la même relation, l'auto-réfence,
etc. Il manque un seul ingrédient pour que le problème survienne
: la négation !
C'est pareil pour le Paradoxe du Menteur. La phrase "Je
dis la vérité" ne pose aucun problème, car
il n'y a aucune négation, de mot "NON"
caché quelque part. Mais ce n'est pas pareil avec la phrase
"Je mens" ! Car dans le mot "mentir" il y a le mot "NON",
ici la négation de la vérité ou
du vrai. C'est sur la négation que toute l'attention
doit porter. (voir les documents L'anatomie
de la Contradiction,
La logique
des Shadoks, Le problème
de la Négation, Le
principe d'Alternation). Quel genre de négation fait-on
en science ? D'elle dépend entre autres la nature de la notion
d'ensemble.
L'artifice
du porc et cochon
Ce
qui est intuitivement et philosophiquement désagréable, c'est
que la notion d'ensemble serve à rassembler
les objets vérifiant une propriété ou un attribut donné, mais
pas l'attribut que la notion est elle-même ! Pourquoi pas l'ensemble
de tous les ensembles, exactement comme on parlerait
de l'ensemble de tous les nombres entiers naturels, de l'ensemble
de tous les humains ou de l'ensemble de toutes les étoiles
? Si la notion d'ensemble ne rassemble pas elle-même, elle
a un problème d'existence, car par exemple si l'ensemble de
tous les humains n'existe pas, alors c'est que les humains
n'existent pas. Et au pire, si aucun humain n'existe, l'ensemble
de tous les humains est alors simplement l'ensemble
vide, qui
lui existe. Et plus généralement, si aucun objet ne vérifie
un attribut ou une propriété donnée, alors l'ensemble de tels
objets est simplement vide, et c'est le pire cas d'ensemble
qu'on puisse avoir. Mais dire que des objets vérifiant une
propriété donnée existent tandis que leur ensemble n'existe
pas, est quelque chose de psychologiquement insupportable,
il faut l'avouer. Ou alors la vraie "pathologie" n'est pas
où l'on pense, si on trouve cela normal, et que l'on bâtit
un système d'axiomes légiférant cette situation.
Les
axiomes de ZF par exemple permettent d'introduire une notion
périphérique
celle de collection. Une collection est
la simple donnée d'une relation à un argument ou propriété
P(x). Tous les ensembles vérifiant cette
propriété forment une collection,
qui n'est pas nécessairement un ensemble. Par exemple, la
propriété P(x) : "x
= x",
ou P(x) : "IL EXISTE un ensemble qui a x pour
élément", est vérifiée par tout ensemble. Elle définit donc
la "collection de tous les ensembles",
notion qui doit remplacer celle d'"ensemble
de tous les ensembles". On voit donc qu'il
y a bel et bien une nécessité de pouvoir regrouper en un
tout tous les objets vérifiant une même propriété donnée.
C'est cette notion que l'on désigne intuitivement par le
mot "ensemble". Mais que l'on soit
obligé d'introduire un autre mot qui dit fondamentalement
la même chose, que l'on doit séparer du premier, juste pour
éviter des paradoxes, fait de ce système d'axiomes un simple
art de séparer porc et cochon !
Et non seulement cela, ce système ne résout pas vraiment
le fond problème (c'eût été un moindre mal si ce "jeu de
mots" avait vraiment suffit), car rien n'empêche la pensée
de pousser la question en avant pour poser cette fois-ci
avec la même pertinence le problème de la "collection
de toutes les collections" ! Quel mot faudrat-t-il
cette fois-ci introduire avec le même genre d'artifices pour
"éviter" ce paradoxe ? Le mot classe pour parler de "classe
de toutes les collections" ?
Il
y a actuellement en théorie axiomatique des ensembles
certaines notions orphélines de leur ensemble, à commencer
par la notion d'ensemble elle-même, qui ne possède
pas d'ensemble pour rassembler les objets répondant à cet
attribut. Beaucoup de propriétés P(x) sont
ainsi privées du droit d'avoir un ensemble pour rassembler
les objets qui les satisfont. Etre un "ensemble qui
n'appartient pas à lui-même", un ordinal,
un cardinal, etc. font partie des propriétés
ainsi orphéline. On peut croire que le problème
est résolu dès lors qu'on leur a trouvé un
père ou une mère adoptive appelée "collection",
pour les rassembler, comme une poule rassemble ses poussins
sous elle. Mais il n'en est rien, car cette poule est elle-même
orphéline de la même façon, à un
autre niveau. Or il est très important que la notion
d'ensemble s'applique à elle-même, car c'est ainsi
qu'elle livre ses plus grands secrets, et même tous simplement
les plus grand secrets de l'Univers ! Car
c'est en fait l'Univers, le TOUT,
qui se cache derrière l'ensemble
plein, l'ensemble de tous les ensembles.
La logique actuelle, à cause des bases sur lesquelles
elle repose (et en particulier le fameux principe
de non-contradiction),
est trop
faible pour appréhender, les propriétés
très spéciales
très importantes de l'Univers. Résoudre
ce problème et restaurer l'ensemble plein (l'Univers donc...)
à la place de droit, telle est la raison d'être
de la Théorie
des univers. Poursuivons le diagnostic avec d'autres
très importantes notions de la théorie des ensmbles,
comme par exemple la notion d'ordinal.
Le
Paradoxe de Burali-Forti
Dans
l'exposé du Paradoxe de Russell, c'est à dessein que j'ai
choisi d'appeler alpha (ou
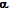 )
ces ensembles qui "n'appartiennent pas à eux-mêmes".
Car la tradition actuelle est de désigner par une lettre grecque
un ordinal.
Le Paradoxe
de Burali-Forti* est
le paradoxe du plus grand ordinal ou du dernier ordinal.
Il concerne
donc les ordinaux,
et plus précisément l'ensemble (appelons-le encore une fois
A) de tous les ordinaux.
)
ces ensembles qui "n'appartiennent pas à eux-mêmes".
Car la tradition actuelle est de désigner par une lettre grecque
un ordinal.
Le Paradoxe
de Burali-Forti* est
le paradoxe du plus grand ordinal ou du dernier ordinal.
Il concerne
donc les ordinaux,
et plus précisément l'ensemble (appelons-le encore une fois
A) de tous les ordinaux.
Un ordinal 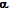 est
un ensemble spécial possédant un certain nombre de propriétés
très importantes, dont celles-ci, qui sont au coeur du
Paradoxe de Burali-Forti :
est
un ensemble spécial possédant un certain nombre de propriétés
très importantes, dont celles-ci, qui sont au coeur du
Paradoxe de Burali-Forti :
Alpha 1 : La
relation d'appartenance est une relation de bon ordre strict
dans un ordinal; grosso modo cela veut dire que ses éléments
sont ordonnés avec la relation d'appartenance ( )
très exactement comme les nombres entiers naturels le
sont avec la relation d'infériorité stricte (<),
et que quand on puise n'importe quelle quantité des éléments
d'un ordinal, il y a
toujours
parmi eux un qui est plus petit que tous les autres. D'ailleurs,
dans une théorie axiomatique classique comme celle de
ZF, les nombres entiers naturels sont les tout premiers de
la famille des ordinaiux; mais il ne faut surtout pas confondre
ces deux notions en général, car si un entier
naturel est un ordinal particulier, un ordinal n'est pas forcément
un entier naturel. Mais il suffit d'abandonner le principe
de non-contradiction qui est à l'origine de tout
cela, de
changer donc de logique (et plus précisément
de négation)
pour que la notion d'ordinal et celle de nombre
entier naturel deviennent simplement la même chose.
Et même, tout ensemble devient un ordinal !
En fait, c'est une
négation anormale qui fait qu'on sépare ce
qui ne devait jamais être séparé.
Et c'est la résolution de cette
anomalie qui commence ici et avec la Théorie des
univers. Mais pour l'instant, parlons des choses telles
qu'elles
sont dans
les théories des ensembles faites avec la logique
classique, comme ZF...
)
très exactement comme les nombres entiers naturels le
sont avec la relation d'infériorité stricte (<),
et que quand on puise n'importe quelle quantité des éléments
d'un ordinal, il y a
toujours
parmi eux un qui est plus petit que tous les autres. D'ailleurs,
dans une théorie axiomatique classique comme celle de
ZF, les nombres entiers naturels sont les tout premiers de
la famille des ordinaiux; mais il ne faut surtout pas confondre
ces deux notions en général, car si un entier
naturel est un ordinal particulier, un ordinal n'est pas forcément
un entier naturel. Mais il suffit d'abandonner le principe
de non-contradiction qui est à l'origine de tout
cela, de
changer donc de logique (et plus précisément
de négation)
pour que la notion d'ordinal et celle de nombre
entier naturel deviennent simplement la même chose.
Et même, tout ensemble devient un ordinal !
En fait, c'est une
négation anormale qui fait qu'on sépare ce
qui ne devait jamais être séparé.
Et c'est la résolution de cette
anomalie qui commence ici et avec la Théorie des
univers. Mais pour l'instant, parlons des choses telles
qu'elles
sont dans
les théories des ensembles faites avec la logique
classique, comme ZF...
Alpha 2 : Un ordinal ne
peut pas appartenir à lui-même; une
conséquence de Alpha 1, et
précisément la caractère strict de
l'ordre, qui implique fortement la négation;
elle brise la réflexivité d'une
relation d'ordre normale, c'est-à-dire le fait que l'ordre
s'applique à soi-même, le fait d'être plus grand ou plus petit
que soi-même ! En fait, les ordinaux sont les ensembles
cachés derrière les ensembles alpha du
Paradoxe de Russell : 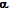

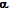 .
La propriété clef qui est la cause du paradoxe est justement de le fait de NE PAS appartenir à soi-même (et
non pas d'apparternir à soi-même, qui ne pose
aucun problème) car justement c'est
la négation qui pose problème.
.
La propriété clef qui est la cause du paradoxe est justement de le fait de NE PAS appartenir à soi-même (et
non pas d'apparternir à soi-même, qui ne pose
aucun problème) car justement c'est
la négation qui pose problème.
Alpha 3 : Tout ordinal est
transitif;
ce qui signifie que les éléments de ses éléments sont
aussi ses éléments; une conséquence de
Alpha1, mais précisément de la transitivité de
la relation d'ordre, mais pas nécessairement de son obligation
d'être strict,
qui, elle, est lié au problème
de la négation.
Alpha
4 : Tout ensemble transitif d'ordinaux est un ordinal;
une sorte de réciproque de Alpha 3; si donc un ensemble dont
tous les éléments sont des ordinaux, et tel que les éléments
de ses éléments
sont aussi ses éléments, alors cet ensemble est
un ordinal.
Alpha
5 : Les éléments d'un ordinal sont tous des ordinaux ;
une conséquence de toutes les propriétés précédentes.
De
toutes ces propriétés il découle tout simplement que l'ensemble
A de tous les ordinaux doit
être un ordinal, et il est le dernier
d'entre eux, puisque tous lui appartiennent (ce qui chez
les ordinaux signifie que tous lui sont inférieurs). Mais
si A est un ordinal,
il appartient à lui-même, puisqu'il est par définition l'ensemble
de tous les ordinaux. Cela contredit alors Alpha
2, qui interdit à un ordinal d'appartenir à lui-même; d'où
le
Paradoxe de Burali-Forti.
Mais
comme expliqué dans les commentaires accompagnant Alpha 1 et
Alpha 2, il ne s'agit que d'une autre forme du Paradoxe de
Russell. Car les ordinaux sont les cas fondamentaux de ces
ensembles alpha qui (à cause de la négation actuelle) ne doivent
pas appartenir à eux-mêmes : 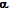

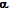 .
.
La
philosophie de la Théorie des univers
Avant de comprendre
que le vrai problème des paradoxes est le problème de la négation,
la Théorie des univers (élaborée entre 1998 et 2003 avant de
de devenir la Théorie
universelle des ensembles puis la Science
de l'Existence depuis 2003) a tenté de résoudre ces problèmes
de manière axiomatique, mais toutefois
en s'éfforçant
d'en
avoir
recours le moins possible. Je me suis efforcé d'exhiber le
plus possible des modèles naturels (voir Le
modèle universel ci-dessous) satisfaisant
les axiomes de ZFC, ne posant en axiome que ce
que je ne pouvais pas démontrer à l'époque.
L'objectif de la Théorie
des univers était avant tout de trouver le moyen de restaurer
l'ensemble plein en théorie des ensembles,
tout en évitant les paradoxes ou en essayant de bien comprendre
leur nature et leur mécanisme, afin d'y apporter la meilleure
réponse. Dans le meilleure des cas (pensais-je), on pouvait
les résoudre (ce que j'espérais faire) et dans le pire, ils
n'étaient
pas
si dangereux qu'on le pensait. L'axiome de l'ensemble plein
pouvait cohabiter d'une certaine manière avec les autres axiomes.
J'avais cette conviction, et il fallait trouver le moyen de
la concrétiser.
Pour cela, à la manière
du vaccin qui consiste à introduire volontairement le virus
affaibli dans l'organisme pour lui apprendre à lutter contre
le mal, il fallait utiliser les paradoxes eux-mêmes et leurs
enseignements au sein même de la nouvelle théorie, pour la
rendre plus forte contre eux. L'idée était simple : créer dans
la théorie des ensembles des ensembles très spéciaux U appelés
univers, qui à leur niveau sont ce que la
collection  (ou
Oméga
(ou
Oméga 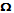 )
tout entière des ensembles est. Autrement dit, il fallait définir
des ensembles U qui, munis de la relation
d'appartenance
)
tout entière des ensembles est. Autrement dit, il fallait définir
des ensembles U qui, munis de la relation
d'appartenance  dans
dans  ,
vérifient les mêmes axiomes que
,
vérifient les mêmes axiomes que  ,
ou des axiomes suffisamment essentiels pour qu'on puisse appeler
l'ensemble U une "théorie des
ensembles" ou UN "ensemble de tous
les ensembles". Les éléments de U sont
appelés les ensembles au sens de U,
à différencier des ensembles au sens général, à savoir au sens
de l'Univers général
,
ou des axiomes suffisamment essentiels pour qu'on puisse appeler
l'ensemble U une "théorie des
ensembles" ou UN "ensemble de tous
les ensembles". Les éléments de U sont
appelés les ensembles au sens de U,
à différencier des ensembles au sens général, à savoir au sens
de l'Univers général  dans
lequel U est plongé. Ainsi, donc, à défaut
que
dans
lequel U est plongé. Ainsi, donc, à défaut
que  soit
un ensemble (donc L'ensemble de tous
les ensembles), il
a en lui des espéces de clones de
lui-même ou des versions de lui-même qui eux le sont, qui sont
DES ensembles de tous les ensembles, le premier
mot "ensemble" qui apparaît dans cette
expression étant au sens général du terme dans
soit
un ensemble (donc L'ensemble de tous
les ensembles), il
a en lui des espéces de clones de
lui-même ou des versions de lui-même qui eux le sont, qui sont
DES ensembles de tous les ensembles, le premier
mot "ensemble" qui apparaît dans cette
expression étant au sens général du terme dans  ,
et le second mot "ensemble" signifiant
"ensemble
au sens de U" ou simplement "élément
de U". Cela permet ainsi de n'utiliser qu'un seul
mot "ensemble", qu'une seule relation
d'appartenance, qu'un seul langage, etc., et pourtant
d'obéir à la différenciation entre "porc et cochon",
nécessaire pour ne pas tomber dans les paradoxes.
,
et le second mot "ensemble" signifiant
"ensemble
au sens de U" ou simplement "élément
de U". Cela permet ainsi de n'utiliser qu'un seul
mot "ensemble", qu'une seule relation
d'appartenance, qu'un seul langage, etc., et pourtant
d'obéir à la différenciation entre "porc et cochon",
nécessaire pour ne pas tomber dans les paradoxes.
Si un ensemble U appartient
à un autre ensemble V,
on a tout à fait le droit de faire la différence entre les
notions d'élément de U et
celle d'élément
de V. Cela n'est pas intuitivement choquant comme
l'affaire de la séparation des mots "collection"
et "ensemble", puisqu'ici, que l'on
parle de U, de V, des éléments
de U ou des éléments de V (dont U),
on parle toujours des ensembles. Il suffit maintenant de
s'arranger
très astucieusement pour ce que U et V aient
des propriétés spéciales communes (celle d'univers justement),
qui les rendent semblables à l'Univers général  .
Et de cette façon, on peut dire d'une certaine façon, que
.
Et de cette façon, on peut dire d'une certaine façon, que  est
un ensemble (via U ou V),
qu'il appartient à lui-même, propriété que doit posséder
l'ensemble
de tous les ensembles. Les propriétés de
est
un ensemble (via U ou V),
qu'il appartient à lui-même, propriété que doit posséder
l'ensemble
de tous les ensembles. Les propriétés de  en
tant qu'ensemble qu'on ne pouvait pas étudier ou connaître,
on peut maintenant les étudier et les connaître à travers
ses clones que sont les univers, les ensembles
du genre U et V. Je n'en
avais pas conscience à l'époque, mais ce que j'étais en train
d'élaborer ainsi était simplement une structure
fractale de l'Univers
en
tant qu'ensemble qu'on ne pouvait pas étudier ou connaître,
on peut maintenant les étudier et les connaître à travers
ses clones que sont les univers, les ensembles
du genre U et V. Je n'en
avais pas conscience à l'époque, mais ce que j'étais en train
d'élaborer ainsi était simplement une structure
fractale de l'Univers  .
L'Univers
.
L'Univers
 tout
entier qui re répète infiniment en lui-même
et à toutes les échelles. C'était
la simple solution aux problèmes des paradoxes.
tout
entier qui re répète infiniment en lui-même
et à toutes les échelles. C'était
la simple solution aux problèmes des paradoxes.


Un simple exemple de construction d'une Fractale :
1) Au départ, Carré Rouge ou Vert;
2) Diviser le Carré en 9 plus petits Carrés; inverser
la couleur du Carré du milieu : s'il est noir il devient
blanc et vice-versa;
3) Répéter l'opération
précédente pour chacun des 9 nouveaux petits Carrés;
et ainsi de suite.
L'auto-référence;
être différent d'un autre tout en étant
pourtant l'autre; appartenir à soi-même
tout en n'appartenant pas à soi-même;
ne pas être le dernier ordinal tout en l'étant
pourtant; ne pas être l'ensemble de tous
les ensembles tout
en l'étant pourtant, etc.; autant
de phrases "contradictoires",
qui ne le sont pas en fait. Le secret se trouve dans
la structure fractale ! Il ne faut plus que la notion
de fractale et d'autres (comme par
exemple aussi la relation d'équivalence)
soient objets d'une d'une logique ou d'une science
fondée sur un principe étriqué (le principe
de non-contradiction)
où toute leur puissance et leur toute-puissance
est
étouffée, et où leurs caractéristiques
profondes et sublimes sont appelées des "paradoxes" ou "contradictoires".
Mais il faut que toute la logique ainsi
que toute la science repose désormais
sur le paradigme de la structure fractale.
Le principe qui fonde une telle logique est le principe
d'alternation, et la logique associée est
la Logique
Alternative.
Le
modèle universel
Je le nomme A' 6
parce que comme on va le voir plus loin, il ne s'agit que
de la forme ultime de l'axiome de l'infini. Toute la question
est de trouver la voie d'intégration de cet axiome
dans le système d'axiomes de ZFC. C'est un axiome
de
nature "incompatible" avec les autres, certes,
mais il s'agit de comprendre vraiment pourquoi. Il faut trouver
la cause exacte du problème afin de trouver enfin
la voie de la compatibilité. Cette voie était
en fait inscrite dans une très agréable découverte
faite en 1987, et qui m'a fait nourrir l'espoir que tous
les axiomes de ZFC pouvaient être démontrés
d'une manière très naturelle. Autrement dit,
le théorie des ensembles ne devait pas être
un système
d'axiomes (d'où le mot axiomatique)
mais un système
de théorèmes (d'où mot théorématique).
La démonstration fut faite en effet pour tous les
axiomes, sauf un, qui résistait à cette méthode
de démonstration et
pour cause : c'est une méthode finitiste, une méthode
reposant sur une construction finie, celle que je vais brièvement
exposer ci-après.
Nous
allons construire un modèle de théorie
des ensembles, appelé le modèle
universel (et pour cause !), satisfaisant naturellement
tous les axiomes (donc qui les transforme
en théorèmes)
sauf celui de l'infini. Et à partir de ce modèle
universel, nous allons dans un second temps voir
comment bâtir un grand modèle (l'Univers tout
simplement) satisfaisant cette fois-ci tous les axiomes
de ZFC (plus
l'axiome de
fondation
A7),
et
au-delà ! En effet, l'Univers doit satisfaire A'6,
le super-axiome de l'infini ! En effet,
ce super-axiome devenu un théorème (par
les vertus de la méthode théorématique que
l'on voit ainsi progressivement à l'oeuvre), les
paradoxes comme ceux de Russell (paradoxe de l'ensemble
des ensembles non-éléments d'eux-mêmes),
de Burali-Forti (paradoxe de l'ensemble de tous les
ordinaux ou
du dernier
ordinal), bref l'ensemble de tous les paradoxes, disparaissent
purement et simplement ! Autrement dit, ces paradoxes ne
seront plus des contradictions au
sens actuel du terme, c'est-à-dire au sens de la
logique fondée sur le principe
de non-contradiction. Mais ces paradoxes
seront
de
simples inoffensifs
théorèmes au sens d'une nouvelle
logique, obéissant à un
principe supérieur, le principe
d'alternation. On sera alors passé de l'axiomatique à
la théorématique. Le mode
d'emploi commence par le modèle universel qu'on
va découvrir maintenant.
La
structure physique des ensembles
On se donne
deux symboles quelconques, par exemple 0 et 1 ou
a et b, ou encore les symboles "{" et "}".
Le premier est appelé "parenthèse ouvante" et
le second "parenthèse
fermante". Le but est de réaliser avec ces parenthèses
tous les assemblages d'un type très spécial, appelés
les "parenthésages" ou les "assemblages
ensemblistes" ou simplement "ensembles",
qui sont ni plus ni moins les structures possibles de parenthèses.
Si on considère par exemple l'expression : (x + 2)((x - 7)² +
4(x - 5)) et qu'aux
parenrhèses dans cette expression, elle a la structure suivante
: ( )(( )( )), qui est aussi en écritrure
binaire le
nombre de huit bits suivant : 01001011;
ou encore, si on adopte un alphabet de seulement deux lettres a et b,
cette même structure s'écrit comme le mot de huit lettres suivant
: abaababb. C'est à ce type de structure de
très grande importance qu'on va s'intéresser maintenant, car
elle cache de très grands secrets de la notion d'ensemble,
de ce qu'il faut appelée un "ensemble".
Ici commence une construction physique de cette
notion, ici commence la compréhension de la nature de l'Univers au
sens physique du terme, la découverte de ses
profonds secrets. Ici on va construire un modèle élémentaire
de l'Univers, un modèle universel,
ou simplement un univers.
Tous les "ensembles" en ce sens-là sont
obtenus par récurrence avec les règles suivantes
:
E1) L'assemblabe {
} ou 01 ou ab formé de
la parenthèse
ouvrante et fermante est un ensemble,
appelé par définition l'ensemble vide,
noté 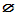 .
.
E2) Si A est un ensemble,
alors l'assemblage {A} obtenu en prenant
en sandwitch l'assemblage a entre les parenthèses,
est un nouvel ensemble, appelé un
singleton. A est appelé l'élément de
ce singleton {A}.
E3) Si A et B sont deux ensembles,
alors l'assemblage AB obtenu en concaténant
simplement A et B, est
un nouvel ensemble appelé la réunion de A
et B.
Tous les éléments de A et B
sont aussi appelés les éléments de AB.
E4) Tous les ensembles sont obtenus par
application répétée
des règles précédentes.
L'ensemble (au
sens intuitif du terme) de ces parenthésages (ou
"ensembles"au
sens nouveau du terme) est appelé le modèle
universel ou l'univers de base
ou encore l'univers de référence.
On l'appelle l'Oméga et on le note 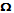 .
Avec l'ensemble vide
.
Avec l'ensemble vide 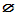 ,
ils constituent les deux exemples fondamentaux d'une notion
générale, la notion d'univers,
qui sera très précisément définis à partir d'eux. Un univers sera
noté de façon générale U,
ou par les lettres U, V, W,
etc. On connaît donc déjà deux exemples importants de cette
notion, qui serviront à créer tous les autres, selon une
structure spéciale et très importante, la structure fractale (on
y reviendra).
,
ils constituent les deux exemples fondamentaux d'une notion
générale, la notion d'univers,
qui sera très précisément définis à partir d'eux. Un univers sera
noté de façon générale U,
ou par les lettres U, V, W,
etc. On connaît donc déjà deux exemples importants de cette
notion, qui serviront à créer tous les autres, selon une
structure spéciale et très importante, la structure fractale (on
y reviendra).
Il est
très facile de démontrer que tout ensemble
A est de la forme : A1 A2 A3 ...
An, où Ai est
soit un singleton, soit l'ensemble
vide. Et l'assemblage
} { , qui n'est pas un ensemble, est appelé une virgule ou un séparateur,
et est noté "," . Cela
fait qu'un ensemble de la forme {A1}
{A2} {A3} ... {An} peut être noté : {A1,
A2, A3, ... , An}; on définit ainsi très
rigoureusement la notion habituelle des ensembles
finis, ainsi que leur notation, qui n'est plus une
simple convention, mais traduit la structure physique de
l'ensemble en question.
L'égalité
et l'équivalence
Dans l'absolu,
deux ensembles A et B sont
égaux s'ils sont exactement le même
assemblage de parenthèses, donc le même nombre
binaire écrit
avec les deux bits 0 et 1,
ou encore le même mot dans l'alphabet dont les seules
deux lettres sont a et b.
Cette
égalité est la conception
classique de cette notion, qui dit que toute chose X n'est
égale qu'à elle-même
: X
= X. Cette égalité basique est très
importante, mais il faut la mettre à sa juste place,
sinon on fait une science très pauvre et aveugle. Le
fameux principe
de non-contradiction formulé par Aristote et
très fondamental dans le paradigme scientifique actuel,
interdit par exemple que l'on dise que deux choses différentes puissent
être égales en même temps.
Ainsi par exemple, à partir du moment où j'ai
posé que 0 et 1 ou a et b qui
me servent à faire la présente étude
sont des objets différents,
je n'ai plus le droit avec ce principe de dire que ces deux
objets sont égaux. Et pourquoi donc
? C'est moi qui ai décidé de
les distinguer quand je juge
nécessaire de les distinguer, et
donc c'est moi aussi qui décide de ne
plus les distinguer,
quand je juge nécessaire de ne plus les distinguer.
Je peux par exemple dire que moi à 50 ans je suis différent du bébé que
j'étais à ma naissance, que lui et moi nous ne sommes pas
le même être, j'ai raisons bien justifiées
de faire cette distinction. Mais je peux tout aussi bien
dire en montrant mon album de photos d'enfance à des
amis que ce bébé et moi nous sommes le même être;
et j'ai aussi de bonnes raisons de ne pas faire de distinction
entre lui
et moi. Ainsi donc, selon le contexte où la nécessité,
nous sommes le même être ou nous ne le sommes
pas. En d'autres termes, selon le contexte je suis égal à moi-même
ou différent
de moi-même. Et d'une manière générale,
selon le contexte ou ce que je veux exprimer, a est
a ou a
est différent de a. Autrement dit encore,
selon le contexte, je distingue a et b ou
je peux décider de mettre fin à cette distinction
et de les voir comme le
même être. C'est bien ce que
l'on fait avec la variable X par exemple.
On écrit tantôt X = 0, tantôt X
= 1, etc. (voir le document La
Théorie axiomatique des ensembles : la fausse solution
!).
Ce faisant, je décide simplement quand X est
égal à 0,
donc
différent de 1,
et quand au contraire X est égal à 1.
L'égalité stricte (de
type 0 = 0, 1 = 1, bref a
= a), est étroitement liée
au principe
de non-contradiction.
Elle n'est qu'un cas particulier d'une conception plus large
et universelle de l'égalité,
qui est la relation d'équivalence.
L'égalité stricte a = a (et
le principe
de non-contradiction qui
lui est équivalent) donne une science pauvre et très
handicapée
si on se limite à elle. Mais en revanche l'équivalence est
une conception de l'égalité infiniment
plus large, plus puissante et plus féconde. Elle commence
là où l'on se donne des critères pour
dire de deux choses différentes a et b qu'elles
sont la même
chose, et on a des raisons de le dire. En effet,
deux choses a et b ont
toujours quelque chose en commun qu'on appellera
c, une certaine propriété
commune c ou un certain attribut commun
c;
et à défaut, il s'agit de l'attribut
commun c que toutes les choses ont, à savoir
justement la qualité de chose (voir Chose,
Existence, Ensemble). Et au regard de cette chose c qu'elles
ont en commun, a et b sont égales;
on dira qu'elles sont égales modolo c. Par exemple, deux
humains a et b sont égaux au
regard de leur qualité
commune d'humain, mais vont se différencier
sur d'autres
critères, les critères propres (la couleur, la
taille,
le sexe, etc.). Et deux humains de même couleur sont aussi
parfaitement égaux au vu des critères humain et couleur,
et vont se différencier sur d'autres, etc. Et selon que
l'on considère ce qui est commun à a et b ou
au contraire ce qui les différencie, on décide que a et b sont
la même
chose ou deux choses différents. C'est ainsi
par exemple que deux électrions ou deux protons
a et b, sans aucune autre précision ou critère
de
différenciation, sont jusqu'à nouvelle ordre le même
électron ou le même
proton. Et si on dit que a et b sont distincts sans
dire pourquoi, cela sous-entend un certain critère de différenciation.
Et à tout
moment on peut décider de ne plus tenir compte de ce critère mais
de ne regarder
que ce qui fait l'unité ou l'unification de a et b.
C'est
ainsi que l'on fait la science avec l'équivalence,
notion d'égalité infiniment plus puissante que
la stricte égalité a
= a. L'équivalence signifie forcément
qu'on ne fonctionne plus avec le principe
de non-contradiction,
qui limite à la seule stricte égalité 0 = 0, 1
= 1, a = a, b = b, et qui appelle
une "contradiction" le fait
de dire : 0 = 1 ou a
= b. L'équivalence est très liée à la
notion d'ensemble dont justement
nous sommes en train d'étudier l'anatomie la plus profonde, car parler
de "propriété
commune c", d'"attribut commun c",
etc., que a et b possèdent, c'est
simplement parler d'un certain ensemble c auquel a et b appartiennent.
En effet, un ensemble est défini par une certaine propriété
caractéristique que partagent tous ses éléments.
On dira donc de deux éléments a et b d'un
certain ensemble
c, qu'ils sont égaux modulo c. Et l'ensemble
c est appelé une classe d'équivalence ou
une classe
d'égalité. La notion d'ensemble est
tout simplement la notion générale de classe d'équivalence ou classe
d'égalité. C'est une des nombreuses manières
de définir
la notion d'ensemble. Et la classe d'égalité la
plus grande qui soit est la classe Univers, et la propriété
caractéristique de ses éléments est la notion
de chose .
Deux choses a et b partagent
cette propriété commune miminale, cet attribut
commun fondamental, qui est la qualité de chose !
C'est elle qui soude toutes les choses, les rassemble ou
les assemble pour faire la chose spéciale appelée l'Univers,
qui est par définition l'Ensemble de toutes les choses (voir Chose,
Existence, Ensemble).
L'Univers est
le problématique Ensemble plein que
nous sommes
justement en train d'étudier ici, nous sommes en train de comprendre
pourquoi on ne doit pas parler de l'axiome de l'ensemble plein A'6
: " Il
existe un ensemble ayant tout ensemble comme élément".
Mais en fait, nous avons déjà un début de réponse à la
question (pour ne pas dire toute la réponse), car cela tient au principe
de non-contradiction et
à la conception de l'égalité qui lui est liée, à savoir
seulement l'égalité
stricte, du type : 0 = 0, 1 = 1, a
= a, b = b. Par conséquent, avec la notion
d'égalité qui
commence maintenant, avec la relation d'équivalence que
nous allons définir à présent (et qui généralise
l'égalité
stricte), commence aussi l'abandon du principe
de non-contradiction !
Nous commençons ainsi à entrer dans un principe plus fort, l'alternation,
qui lui est très lié à l'équivalence.
Nous commençons à abandonner l'axiomatique pour
la théorématique, car à la clef tout
sera démontré
et on n'aura plus besoin de faire la science avec des axiomes ou
des hypothèses.
L'équivalence
entre deux ensembles
Aussi étonnant
que cela puisse paraître, avec le modèle
universel que
nous venons de définir, c'est-à-dire avec l'ensemble 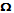 (au
sens pour l'instant intuitif du terme) que nous venons de
construire par récurrence, nous avons aussi défini
tout ce qu'il faut appeler un ensemble ! Tous
les ensembles possibles et imaginables ont été construits
! Nous avons donc l'Ensemble de tous les ensembles (ou
Ensemble plein), et même bien plus
que cela : nous avons construit toutes les choses de
l'Univers, nous savons comment elles sont
faites physiquement ! Il a suffi pour cela d'avoir fait cette
simple récurrence. Le reste est maintenant
une simple affaire d'équivalence,
et elle aussi sera définie par récurrence !
L'équivalence aura
d'abord pour but de nous donner des critères pour
dire quand on peut dire que deux ensembles A et B (ainsi
construits) sont égaux. Et dans un second temps, la
même
équivalence va nous dire comment obteinir à partir
d'un ensembleA donné
que nous avons construit, un ensemble plus
grand, infiniment plus grand ! Bref elle permettra de construire
par récurrence tous les ensembles, toutes les choses
de l'Univers !
Elles le sont en fait déjà. Mais nous allons
comprendre pourquoi avec l'équivalence...
(au
sens pour l'instant intuitif du terme) que nous venons de
construire par récurrence, nous avons aussi défini
tout ce qu'il faut appeler un ensemble ! Tous
les ensembles possibles et imaginables ont été construits
! Nous avons donc l'Ensemble de tous les ensembles (ou
Ensemble plein), et même bien plus
que cela : nous avons construit toutes les choses de
l'Univers, nous savons comment elles sont
faites physiquement ! Il a suffi pour cela d'avoir fait cette
simple récurrence. Le reste est maintenant
une simple affaire d'équivalence,
et elle aussi sera définie par récurrence !
L'équivalence aura
d'abord pour but de nous donner des critères pour
dire quand on peut dire que deux ensembles A et B (ainsi
construits) sont égaux. Et dans un second temps, la
même
équivalence va nous dire comment obteinir à partir
d'un ensembleA donné
que nous avons construit, un ensemble plus
grand, infiniment plus grand ! Bref elle permettra de construire
par récurrence tous les ensembles, toutes les choses
de l'Univers !
Elles le sont en fait déjà. Mais nous allons
comprendre pourquoi avec l'équivalence...
Il existe
une infinité d'équivalences sur
les parenthésages (les ensembles)
que nous avons définis, l'égalité pure
et simple et au sens strict, étant un cas très particulier.
Avec cette équivalence canonique, l'opération de réunion
que nous avons définie avec la règle E2 n'est pas commutative.
En effet, pour deux ensembles A et B,
les assemblages AB et BA ne
sont pas égaux au sens canonique
du terme. Par
exemple prenons A l'ensemble {{
}} ou 0011 ou aabb et
pour B l'ensemble {{
}{ }}{ } ou 00101101 ou
aababbab. On a : AB = {{
}}{{ }{ }}{ } ou
001100101101 ou aabbaababbab;
et BA = {{ }{ }}{ }{{ }}ou 001011010011ou aababbabaabb,
ce qui n'est pas la même séquence de bits. Donc AB et BA ne
sont pas égaux au sens canonique
du terme, l'opération définie dans E2 n'est donc pas commutative.
Mais on peut vérifier aisément qu'elle est par contre associative,
car (AB)C = A(BC) = ABC, puisqu'on ne touche
pas à l'ordre des ensembles A, B et C dans
cette concaténation.
Là où une
certaine équivalence ou égalité (ici
l'égalité canonique)
interdit la commutativité, on peut
définir une autre qui l'autorise. Il suffit que pour cette
équivalence la permutation de l'ordre dans
une chose donne
une chose aui lui est équivalente.
Et le but est simplement de définir maintenant une équivalence
qui vérifie les propriétés standard de la réunion de deux
ensembles :
R1) A 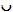
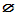 =
A ; l'ensemble vide est l'élément neutre pour la réunion.
=
A ; l'ensemble vide est l'élément neutre pour la réunion.
R2) A 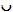 A
= A ; l'idempotence de tout ensemble pour la réunion.
A
= A ; l'idempotence de tout ensemble pour la réunion.
R3) A 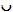 B
= B
B
= B 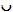 A;
commutativité de la réunion.
A;
commutativité de la réunion.
R4) (A 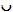 B)
B) 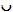 C
= A
C
= A 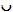 (B
(B 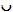 C) ;
associativité de la réunion.
C) ;
associativité de la réunion.
Pour définir
très rigoureusement une équivalence satisfaisant ces règles,
il faut définir un certain nombre de très importantes notions,
qui concernent la structures des ensembles. La première est
la notion de subélément, qui
généralise la notion d'élément d'un
ensemble A. Elle est définie par récurrence
de la manière suivante : A est
appelé le subélément d'ordre
0 de A. Les éléments
de A sont appelés les subéléments
d'ordre 1 de A. Pour un entier
n donné, un subélément d'ordre n
+ 1 de A est un élément d'un subélément d'ordre n de A.
Intuitivement, la notion de subélément traduit le niveau
où se situe une paire de parenthèses ouvrante-fermante dans
les imbrications de parethèses. L'ordre d'un subélément B de
A est aussi appelé la profondeur à
laquelle il se situe dans les imbrications des parenthèses
qui forment A. A lui-même est à la profondeur
0 dans lui-même. Dans le singleton C
= {A},
sa profondeur passe à 1, car il est
un élément de C. Du coup,
la profondeur du subélément B de A augmente
d'une unité dans
C, de deux unités par exemple dans D
= {
}{{A}{
}}, de trois unité dans E = {{
}{{A}{ }}}, etc. Et A est un subélément d'ordre 3 de D,
car il se situe à une profondeur de 3 niveaux
dans D. Il faut ajouter 3 à
la profondeur de tous les subéléments de A,
pour obtenir leur profondeur dans E. Et
quand on navigue dans les profondeurs d'un ensemble A donné,
à un moment donné on tombe forcément sur l'ensemble vide
{ }, puisque la construction des ensembles
a commencé par ce très important ensemble
(règle E1). ceci à lui seul signifie que les ensembles ainsi
construits satisfont l'axiome de fondation A7.
D'autres
définitions assez faciles, dont celle d'une relation
d'équivalence sur ces ensembles,
ainsi qu'une définition d'un ordre spécial
sur
ces ensembles ainsi définis, permet d'introduire la
notion d'égalité entre deux
ensembles. Par exemple, les assemblages { }A et A{
} sont équivalents, ce qui traduit l'idée que la
ré
{
}{ }{ } sont la réunion de trois ensembles
vides. Cet assemblage va équivaloir à {
}.
Ces deux ensembles sont donc "égaux",
modulo cette relation d'équivalence. Et aussi les
assemblages comme A, AA , AAA,
etc., sont équivalents à A.
Et AB et BA sont
équivalents; l'ordre d'assembla
Ces ensembles ainsi
définis avec cette relation
d'équivalence qui permet
de parler de l'égalité entre
deux ensembles, il est très facile de prouver
que ces ensembles satisfont tous les axiomes précédents,
sauf évidemment l'axiome de l'infini A6, puisqu'ils sont
par nature des ensembles finis. Ces ensembles, du fait de
leur caractère fini, satisfont aussi l'axiome de fondation
A7 et l'axiome du choix A8. Il est donc démontré que le
système d'axiomes de ZFC (+ A7) moins l'axiome
de l'infini est un système de théorèmes.
Ceci est un premier pas vers la théorématique,
à savoir une théorie des ensembles dont les énoncés fondateurs
sont tous des théorèmes.
Le seul
véritable axiome sur lequel tous les efforts de démonstration
vont maintenant porter, et surtout qui va livrer les ultimes
secrets des ensembles et de leur structure (déjà bien éclaicie
par la structure des parenthèses), est donc l'axiome de l'infini.
A6. C'est qui, au fur et à mesure de la découvertes des secrets
sur la nature des ensembles, va évoluer vers un axiome nommé
l'axiome des univers, l'unique vrai axiome
et fondateur de la Théorie des univers.
Puis il évoluera pour devenir l'Axiome universel
des ensembles : "Toute chose est un ensemble",
quand un second mot clef le mot chose, sera
adjoint au mot
ensemble. Son corollaire immédiat est A'
6 , l'axiome de l'ensemble plein : " Il existe un ensemble
ayant tout ensemble comme élément". En
effet, on peut définir une chose spéciale,
qui est simplement l'ensemble de toutes les choses.
C'est la définition naturelle et intuitive de l'Univers,
au sens physique du terme. Mais cet axiome a pour conséquence
que l'Univers n'est autre que l'ensemble
de tous les ensembles (ou ensemble plein),
puisque toute chose est un ensemble.
Il pose donc d'office l'existence de l'ensemble plein,
car l'Univers existe ! Il y a
donc un conflit logique entre A'6 et les autres axiomes (maintenant
des théorèmes démontrés par les parenthésages), mais l'existence de l'Univers indique qu'une solution a ce conflit existe !
Et avec
un troisème mot clef, le mot existence emprunté
au quantificateur
existentiel ("IL
EXISTE"), l'Axiome universel des ensembles va
se transformer en Théorème de l'Existence : "Toute
chose existe". Alors cela signifie simplement l'abandon
de l'axiomatique et aussi du principe de non contradiction,
car en fait c'est lui qui posait problème !
Mais revenons
dans la chronologie de la Théorie des univers, pour
découvrir ce que nous apprend son axiome clef, l'axiome
des univers. Il nous montre simplement le secret
de la structure des ensembles, mais aussi de la structure
de l'Univers, qui est simplement une structure fractale :
l'Univers se répète infiniment en lui-même, à la
fois en lui-même et hors de lui-même, à la
fois appartenant à lui-même et n'appartenant
pas à lui-même ! Contradictoire , et pourtant
ce n'est qu'une contradiction apparente; cela s'appelle simplement
une structure fractale ! La solution aux
paradoxes et à tous les problèmes logiques
se trouvent dans cette structure. Et c'est l'axiome
des univers qui va la révéler.
(Ce document n'est pas complet. Je suis sur plusieurs chantiers
de rédaction en même temps. Il est proposé en l'état pour que
le lecteur pressé de savoir de quoi il retourne avec la Théorie
de l'univers, prenne connaissance de l'essentiel
sans attendre
que je l'achève. La version complète
sera proposée dès que possible...)