Définitions des notions clefs de la Science Nouvelle
ou Le nouveau sens des mots de la Science

A

• Absolu et Relatif

La très importante notion d'absolu et de relatif est tout simplement une autre façon de parler de la notion d'ensemble et d'élément. Etant donné un ensemble A, une propriété P est dite absolue dans A et aussi que A est absolu pour P, que si elle est commune à tous les éléments de A. On dit aussi qu'elle est universelle dans A. Dans le cas contraire, on dit qu'elle est relative ou particulière dans A.

Par exemple, le fait d'appartenir à A est une propriété commune à tous les éléments de A. C'est la propriété absolue basique dans A. Pour cette raison, l'ensemble A est absolu pour ses éléments, qui sont alors relatifs à A.

Pour prendre un exemple plus concret, la loi française est une chose absolue pour tous les français, car elle est pour tous les français, qui ont ceci en commun qu'ils doivent y obéir. Mais cette loi n'est pas absolue à l'échelle du monde, et à cette échelle, on dira qu'elle est seulement relative à l'ensemble France. Et à l'échelle de la France, aimer la choucroute n'a rien d'absolu. Mais si on vote une loi obligeant tous les français à aimer la choucroute pour être digne d'être appelé français, d'appartenir à l'ensemble France, on fait de cette chose relative une chose absolue en France, une chose universelle.

L'ensemble le plus absolu qui soit est l'Univers TOTAL (l'Ensemble de toutes les choses), l'Absolu lui-même. Toute chose est relative à cet Ensemble. Les lois communes à toutes les choses, les lois de l'Univers TOTAL, sont les lois absolues, les lois universelles.

• Affirmation et Négation

Dans le langage de la Science Nouvelle, affirmer signifie au sens le plus général : "choisir entre deux choses contraires A et B." Celle choisie est celle affirmée; et l'autre est dite alternée, c'est-à-dire celle à laquelle on a préféré l'autre, l'alter. Les deux choses contraires A et B sont comme le Oui et le Non. C'est pourquoi celle choisie est appelée le Oui, elle celle alternée est appelée le Non. Si par exemple c'est A qui est choisie, alors A est affirmée, elle est le Oui, et B est alternée, elle est le Non; on dira aussi que B est niée. C'est en ce sens uniquement que l'alternation est appelée une négation. Il est très important de distinguer cette négation au sens de l'alternation, qui signifie simplement "opter pour le contraire d'une chose" ou "affirmer le contraire d'une chose", de la Négation au sens négationniste du terme (voir sa définition), qui elle signifie "affirmer le contraire d'une vérité, d'une réalité, refuser à une chose une qualité ou un attribut qu'elle possède, dire par exemple qu'elle n'existe pas alors qu'elle existe, qu'elle n'est pas vraie alors qu'elle est vraie, qu'elle n'est pas possible alors qu'elle est possible, etc."

Considérons par exemple les phrases : A = "Il pleut" et B = "Il ne pleut pas". Dans l'absolu, elles sont deux affirmations, mais des affirmations contraires tout simplement. Si l'on opte pour l'une des deux, celle choisie est celle affirmée et l'autre est celle niée (au sens de l'alternation). A ce stade il est simplement question de dire une chose ou son contraire, il n'est pas question de savoir laquelle des deux phrases est vraie ou fausse, de savoir qui dit la vérité ou qui ment, celui qui dit "Il pleut" ou celui qui dit le contraire, "Il ne pleut pas". Telle que les deux phrases se présentent, la seconde "Il ne pleut pas" est couramment appelée la négation de la première, et on dit qu'elle est la phrase négative tandis que l'autre, "Il pleut", est affirmative. Mais dans l'absolu, les deux sont deux affirmations, et la première, "Il pleut", est aussi la négation de la seconde. Le mot "négation" employé ici signifie simplement que ces deux phrases sont contraires l'une de l'autre, et non pas que l'une ou l'autre nie la vérité, ou que les deux ne peuvent pas être vraies en même temps, etc. Dans le contexte de l'Univers TOTAL (dans l'absolu donc), les deux sont vraies, et si mensonge il y a, c'est le fait de nier cette réalité, ce qui constitue la vraie Négation dans cette affaire, au sens négationniste du terme Négation. Ce n'est pas de cela qu'il est question dans la question d'affirmation et de négation dont il est question avec l'alternation, et qui est une simple affaire de choses contraires.

La notion de négation telle que contenue dans une expression comme "nombre négatif" (par exemple -5) s'inscrit dans ce registre de l'alternation. On a deux versions contraires du même 5, l'un est appelé le positif (comme Oui) est noté +5, et l'autre (l'alterné ou le contraire) est appelé le négatif (comme Non) et est noté -5. Et alterner signifie ici "changer de signe", c'est-à-dire "multiplier par -1". Il s'agit donc ici du postif et du négatif au sens de l'Alternation (voir Positif (1) et le Négatif (1)), à ne pas confondre avec postif et du négatif au sens de la Négation négationniste (voir Positif (2) et le Négatif (2)), qui eux signifent respectivement Bon et Mauvais. Dans ce cas-là, la Science Nouvelle préfère parler de Contraire, d'Antipode ou utliser le préfixe Anti (voir les définitions correspondantes).

Alpha

Terme général qui regroupe tous les mots synonymes de "Anti-Univers": Vide, Rien, Zéro, Point, Particule, etc.

En un sens plus particulier, comme nombre (ou ordinal), il désigne le Zéro, le premier ordinal (le premier nombre), et plus exactement l'Ensemble Vide (ou simplement Vide), habituellement noté 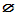. Le contraire de Alpha est Oméga.

• Alter, Alternative, Différence

Le mot "Autre" (en latin "Alter") a une nature particulière dont on n'a sans doute pas mesuré l'importance jusqu'ici. Quelle que la langue considérée, le mot qui signifie "Autre" a un double sens, c'est un mot qui à fois signifie "semblable" et "différent".

Par exemple, dans une conversation, quelqu'un peut dire : "Un homme habillé en blanc est entré dans la pièce où se trouvait une femme; il est suivi plus tard d'un autre homme, habillé lui en noir. L'un d'eux s'est adressé à la femme." Et l'interlocteur demande à celui qui narre les faits : "Lequel des deux s'est adressé à la femme, celui habillé en noir ?" Et le narrateur de répondre : "Non, pas lui, mais l'autre homme."

Dans cette conversation, le narrateur dit que la chose qui est entrée la première dans la pièce où se trouvait la femme est un homme; et en disant qu'il est suivi plus tard par un "autre homme", il dit que la seconde chose entrée après la première est elle aussi un homme, elle est semblable à la première au regard de la qualité ou l'attribut d'homme. C'est donc le mot "autre" dans son sens de "semblable". Puis quand on lui demande si c'est l'homme habillé en noir qui s'est adressé à la femme, en répondant : "Non, pas lui, mais l'autre homme", il emploie le même mot "autre" pour souligner cette fois-ci la "différence" entre les deux hommes, par exemple l'un identifiable par son habit blanc et l'autre son habit noir.

Donc le mot "Autre" (ou "Alter") a la particularité de souligner à la fois ce qui est commun à deux choses A et B et les rend semblables, et aussi ce qui les différencie. C'est ainsi par exemple que le narrateur aurait pu utiliser le même mot "Autre" pour dire qu'un des trois humains est une femme tandis que les autres humains sont des hommes. Cette fois-ci le facteur de similitude est la qualité d'humain et le facteur de différence est le sexe. C'est un mot qui sert à faire une négation d'un type particulier, qu'il faut qualifier de négation relative (voir Négation (1)) et non pas absolue (voir Négation (2)) . Par exemple, en disant : "Non, pas lui, mais l'autre homme", l'un des hommes est nié, mais pas sa qualité d'homme, mais seulement rapport à ce qui le différencie. De même, la qualité d'humain n'est pas niée chez la femme ou chez les hommes de la scène, mais la négation est seulement relative au sexe. La différence entre deux choses A et B est donc cause de négation, mais avec le mot "Autre", cette négation est donc modérée par une qualité commune aux deux choses, qui gomme la différence et fait d'elles la même chose.

Ce type de négation relative qu'est celle du mot "Autre" (ou "Alter") est appelée Alternation. Le mot "Alter" joue un grand rôle dans la Science Nouvelle. Il est appelé le connecteur d'Alternation ou connecteur Différence. Pour toute chose A donnée, on dit qu'une chose B est différente de A si B est une autre chose. Le connecteur Alter et la notion de Différence est la base de la très importante notion de contraire.

Dans une situation où l'on oppose A et B, etc., les deux choses sont appelées des alternatives, B est appelé l'alternative de A (ou l'alter de A), et A l'alternative de B (ou l'alter de B). On note : B = alter A et A = alter B. C'est la définition la plus générale de la notion de contraire (pour plus détails voir la définition de Contraire).

• Alternation, Alternatif

Du verbe alterner, qui au sens le plus général signifie : "raisonner avec le mot autre, le connecteur alter; nier les choses avec le mot alter, avec la notion de contraire." Et au sens plus particulier, alterner signifie : "choisir le contraire d'une chose", "opter pour le contraire d'une chose", "affirmer le contraire d'une chose". L'adjectif "alternatif" signifie "Qui fonctionne selon le paradigme de l'Alternation", comme dans "logique alternative".

Avec l'Alternation, on ne parle que que de chose et de chose contraire, de d'existence et d'existence contraire, de vérité et de vérité contraire, de réalité et de réalité contraire, de possibilité et de possibilité contraire, etc., sans refuser dans l'absolu à la chose contraire la qualité que possède la chose.

Par exemple, (+5) et (-5) sont deux nombres contraires, mais ce sont deux nombres. Le fait pour (-5) d'être contraire à (+5) ne lui fait pas perdre sa qualité de nombre. Et le fait pour (-5) de ne pas être positif (au sens Positif (1)) ne lui fait pas non plus perdre dans l'absolu sa qualité de positif. En effet, il suffit d'inverser (ou justement d'alterner) la convention ou l'orientation pour que ce qui était positif devienne négatif et vice-versa. La symétrie des rôles fait que l'un est potentiellement ce qu'est l'autre, et vice-versa. Ainsi, être négatif c'est simplement être le positif contraire, et être positif c'est être le négatif contraire.

La négation en ce sens de l'Alternation doit maintenant être très soigneusement distinguée de la Négation (au sens 2), la négation au sens de Négationnisme : "Refuser à une chose une qualité ou un attribut qu'elle possède, en particulier la qualité de chose, d'existence, de vérité, de réalité, de possibilité, etc." Pour cela, l'Alternation et la Négation sont deux conceptions très différentes de la négation, elles sont opposées, contraires... L'une est bonne, car elle ne détruit pas dans l'absolu la qualité de la chose niée; et l'autre est mauvaise, car elle détruit dans l'absolu la qualité de la chose (pour plus de détails, voir Négation (2)).

• Anti-chose

Pour une chose A, au sens très général du terme, une anti-chose de A désigne toute chose contraire de A. Mais au sens strict et absolu du terme, ce terme désigne le reste de l'Univers TOTAL, sauf A. Si U désigne l'Univers, l'anti-chose de A est donc U - A; on le note anti A ou -A (pour plus de détails, voir Contraire).

• Anti-Univers, Néant, Vide, Rien, Zéro, Point, Particule, Alpha

Tous ces termes, notés O, sont tous synonymes, ils sont respectivement contraires de : Univers, Existence, Plein, Tout, Infini, Espace, Cosmos, Oméga.

L'Anti-Univers désigne l'Univers TOTAL, U, en tant qu'Elément de lui-même (voir définition Auto-appartenance). En tant que tel, il est a. On a : Anti-Univers = anti U = U - U = O. Mais U - U est aussi ce qui est noté -U (voir définitions Anti-Chose et Contraire).

• Auto, Auto-appartenance, Auto-référence, Réfexivité, Cycle

Désigne la propriété que possède l'Univers TOTAL d'appartenir à lui-même, d'être son propre Elémént. En effet, l'Univers TOTAL, U, est l'Ensemble de toutes les choses; mais U est lui-même une chose, donc est un élément de l'Ensemble qu'il est.

Loi de l'Auto-appartenance de l'Univers TOTAL.

En tant qu'Ensemble (celui qui contient toutes choses et entre autres U lui-même), U est le Plein. Et en tant qu'Elément (celui qui avec toutes les autres choses est contenu dans U), U est le Vide, noté alors aussi O (voir Anti-Univers).

B-C

• Chose

"De la même façon que la notion de 'grain de sable' est l'unité ou quatum du sable, la plus petite quantité de sable, de même la notion de chose est le quatum de l'Univers, l'unité absolue, la plus petite unité. Le rôle du mot chose est d'être le PREMIER de tous les mots, l'Elément absolu; et le rôle du mot Univers est d'être le DERNIER de tous les mots, l'Ensemble absolu. Dans le sable, on compte en grains, et on dit : 0 grain, 1 grain, 2 grains, 3 grains, etc. Mais dans l'Univers, on compte en choses, on dit : 0 chose, 1 chose, 2 choses, 3 choses, etc. "

Le mot chose est le terme le plus général de la Science Nouvelle. "Une chose est tout ce dont on parle"; mais pour dire cela, le mot "ce" cache lui-même tout simplement le mot "chose", de sorte que cette définition dit : "Une chose est toute chose dont on parle".

Le mot chose est donc le mot qui se définit lui-même, la notion la plus fondamentale qui soit, la plus sous-entendue de toutes. C'est le mot clef par défaut, le mot en l'absence de toute autre mot, le mot avant toute autre mot, avant que l'on dise toute autre chose sur la chose considérée. Dans la Science Nouvelle, c'est le nom ou substantif associé au verbe "être", il est un parfait synonyme de "être" en tant que nom, comme par exemple dans "être humain". Et réciproquement, le verbe ETRE est le verbe associé au mot chose.

Dans la Science Nouvelle, le symbole ou mot d'une seule lettre pour dire "chose" est "x"; en majuscule, "Chose" ou " "X". La lettre "Y" quant à elle signifiera : "Autre Chose". Et le symbole pour dire le verve "ETRE" est "=". L'écriture : "X = Y" signifie donc : "X EST Y" ou "Chose EST Autre Chose".

• Constante, Variable

"Au sens le plus universel du terme, une constante est tout simplement n'importe qu'elle chose ! Une constante est un élément, tandis qu'une variable est un ensemble. On utilise le terme constante juste pour dire que l'on considère une chose en particulier, en tant qu'élément, en tant qu'individu. Par opposition donc au fait que l'on considère la chose en général, en tant qu'ensemble."

Considérons par exemple l'ensemble de choses : A = {Pomme, Poire, Mangue, Kiwi, Orange}. Du simple fait d'avoir ainsi défini cet ensemble et de l'avoir nommé A, cela fait de A une variable, dont les éléments sont : Pomme, Poire, Mangue, Kiwi, Orange. Ces éléments sont appelés les valeurs de la variable A, ou ses constantes. On dit que l'ensemble A représente chacun de ses éléments. Ecrire par exemple : A = Mangue, c'est-à-dire une égalité entre l'ensemble et un de ses éléments, s'appelle donner une valeur à la variable, ou la particulariser, ou encore la rendre constante. Car alors elle cesse (provisoirement) d'être une variable pour s'identifier à l'une de ses constantes.

Tout comme on peut selon le besoin appeler un même pays la France ou l'Hexagone, On peut tout à fait donner un autre nom au même ensemble, et dire : B = {Pomme, Poire, Mangue, Kiwi, Orange}. On dit que A et B sont synonymes.

Un ensemble peut tout à fait être aussi l'un de ses propres éléments, donc une variable peut aussi être l'une de ses constantes. Elle est alors dite fractale. l'Univers TOTAL est la plus grande des variables, et toutes les choses sont ses constantes (voir Variable et Infini).

• Contexte, Echelle

Au sens le plus général du terme, un contexte est une chose donnée C, vue comme un ensemble (il faut rappeler que la notion d'ensemble de la Science Nouvelle est une notion physique), comme un espace ou domaine, sur lequel porte un propos ou dans lequel se déroule un propos. On examine les choses telles qu'elles se présentent dans C, on énonce des vérités par rapport à C, on voit la réalité du point de vue de C, telle qu'elle apparaît immédiatement dans C, etc. Cette même réalité peut être très différente, contraire même !, vue d'un autre contexte C'.

Les éléments de cet ensemble C sont appelés les points ou les particules de C. Tout sous-ensemble de C (donc toute partie des points ou éléments de C) est appelé un sous-contexte. L'Univers TOTAL (l'Ensemble de toutes les choses) est le plus grand contexte qui soit, dont toute chose est un sous-contexte. Mais c'est aussi le plus petit contexte qui soit, du fait de sa propriété d'Auto-appartenance et sa structure fractale.

Comme pour tout ensemble physique, c'est nous qui décidons quelles parties d'un contexte C sont des sous-ensembles et lesquelles sont suffisamment petites pour être appelées les éléments de C. Les éléments de C sont à leur tour des contextes, appelés les contextes d'échelle -1, plus petits donc que C. Ces contextes d'échelle -1 ont à leur tour leurs propres éléments, appelés les contextes d'échelle -2, encore plus petits donc que C, etc. On a ainsi les échelles -3, -4, -5, ainsi de suite. On dit que l'on va vers l'infiniment petit de C, à chaque fois que l'on descend d'un niveau dans la structure ensemble-élément.

Dans l'autre sens, en partant de C, on peut considérer un ensemble dont C est un élément, donc qui est plus grand que C. Cet ensemble est un contexte d'échelle +1 par rapport à C. A son tour, il est un élément d'un ensemble encore plus grand, qui est un contexte d'échelle +2, et ainsi de suite. On dit que l'on va vers l'infiniment grand de C, à chaque fois que l'on monte d'un niveau dans la structure ensemble-élément.

• Contraire, Contre, Anti-Chose, Antipode, Anti, Opposé, Symétrique, Alternative

On oppose deux choses sur la base de leur différence. Une chose A peut être opposée à toute autre chose B, ce qui détermine une notion de contraire correspondante.

Par exemple, la notion de Rien peut être opposée à la notion de Quelque Chose, ce qui donne une notion de contraire. Mais la même notion de Rien peut être opposée à la notion de Tout, ce qui est une autre notion de contraire. De même 0 peut-être opposé à 1, tout comme 0 peut être opposé à l'infini. Et 1 peut être opposé non plus à 0 mais à -1. Et de même aussi, on peut opposer 10 à -10, ou plutôt opposer 10 à 1/10 (ou 0,1).

Dans une situation où l'on n'a le choix qu'entre deux choses différentes A et B, où l'on ne se donne comme possibilités que A et B, où l'on oppose A et B, etc., les deux choses sont appelées des alternatives, B est appelé l'alternative de A (ou l'alter de A), et A l'alternative de B (ou l'alter de B). On note : B = alter A et A = alter B (voir plus haut le terme Alter). C'est la définition la plus générale de la notion de contraire.

Pour une chose A donnée, on peut l'opposer à l'Univers TOTAL, U, la chose A étant elle-même incluse dans ce TOTAL. Il s'agit alors d'une opposition de l'élément à l'ensemble, du particulier au général, qui est donc un type de contraire. Mais il existe aussi un autre type de contraire, lui aussi de grande importance, qui consiste à apposer A au reste de l'Univers TOTAL, U. Cela signifie que l'on oppose A à tout l'Univers mais cette fois-ci A lui-même étant exclus de ce TOTAL. On oppose alors A à U - A, et U - A est appelé le contraire de A. On l'appelle l'anti-chose de A, ou l'antipode de A ou anti A, et on le note aussi -A. C'est la définition de la notion de contraire, au sens le plus absolu du terme. Ce terme signifie alors que deux choses sont complètement différentes (comme par exemple le Zéro et l'Infini, ou le Noir et le Blanc), ou par nature opposées, comme (-5) et (+5).

Au lieu d'appeler "nombres négatifs" les nombres comme -1, -2, -3, -4, -5, etc., on aurait pu les appeler de manière plus appropriée "nombres alternes", "nombres contraires", "nombres opposés", "nombres symétriques", "anti-nombres", etc.

D-L

• Dieu, Diable

Dans la Science Nouvelle, le mot "Dieu" désigne tout simplement l'Univers TOTAL, l'Ensemble de toutes les choses, la Chose Suprême. Il suffit d'étudier les propriétés de cette Chose Suprême (Auto-appartenance, structure fractale, Loi de l'Alpha et de l'Oméga, etc.), pour s'apercevoir que ce sont en langage scientifique les attributs fondamentaux que la religion attribue généralement à l'Etre Suprême, Dieu. Autrement dit, Ensemble de toutes les choses et Créateur de toutes choses, sont la seule et même Chose, le seul et même Etre. Il n'y a que le langage qui diffère pour en parler, langage universel des ensembles d'un côté, et langage biblique par exemple d'un côté.

Et la définition scientifique du mot "Diable" est tout simplement tout le contraire de Dieu, le contraire de l'Univers TOTAL, c'est-à-dire l'Anti-Univers, l'Anti-Chose elle-même, l'Anti-Etre. On a : Diable = Anti-Dieu = U - Dieu = -Dieu; et Dieu = Anti-Diable = U - Diable = -Diable.

Derrière l'opposition entre Alternation et Négation, ou entre Logique Alternative et Logique Négative, se cache tout simplement l'opposition entre Dieu et Diable (voir Négation (2)).

• Ensemble et Elémént

"Un ensemble est tout simplement une chose constituée d'aucune, d'une, de deux ou de plusieurs choses, appelées ses éléments." D'une manière très générale, dans cette conception des ensembles (une conception physique), les notions d'élément et de partie (sous-ensemble) sont parfaitement synonymes.

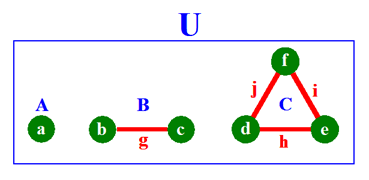
Un ensemble est un une chose U, faite de plusieurs autres choses, appelées ses éléments.
C'est nous qui décidons de voir U comme un ensemble dont les éléments sont : a, b, c, d, e, f, g, h, i, j,
un ensemble dont les éléments sont A, B, C,
un ensemble dont l'unique élément est U,
ou un ensemble n'ayant aucun élément !

En un sens plus restreint, la notion d'élément désignera les parties jugées les plus petites ou les plus basiques de l'ensemble. C'est par exemple nous qui décidons si les cellules d'un humain sont des parties (terme général) ou des éléments (pour signifier "les plus petites parties" de l'humain), si la notion d'élément va commencer avec les molécules (encore plus petites que les cellules), si elle va commencer avec les atomes (encore plus petits que les molécules), si elle va commencer avec les particules (encore plus petites que les atomes), etc.

--> "Un ensemble est dit fractal, s'il est aussi un de ses éléments. On dit aussi qu'il s'auto-appartient."

L'Univers TOTAL est l'Ensemble de toutes les choses. C'est le plus grand des ensembles, il s'auto-appartient, il a une structure fractale (voir Auto-appartenance).

--> "Un ensemble est dit divis ou discret ou quantifié, s'il est subdivisé en parties privilégiées considérées comme ses unités ou quanta. Dans ce cas, ces unités seront de manière privilégiée appelées les "éléments" de l'ensemble, et leur quantité est un nombre entier, fini ou infini. Dans le cas contraire, l'ensemble est dit indivis ou continu ou qualifié."

• Exister, Existence

L'Univers TOTAL, le Tout, l'Absolu, c'est par définition l'Ensemble de toutes les choses. Il découle immédiatement de cette définition que "Toute chose existe dans l'Ensemble de toutes les choses", évidemment, puisque c'est sa définition même ! Ce théorème trivial peut s'exprimer aussi ainsi : "Toute chose existe dans l'Univers TOTAL", "Toute chose existe dans le Tout", "Toute chose existe dans l'Absolu". Sans cette définition précise de l'Univers TOTAL, du TOUT, de l'Absolu, ces déclarations ne seraient qu'une opinion philosophique, un principe posé, un axiome ou une hypothèse. Mais avec la définition de l'Univers TOTAL telle que la nouvelle science le fait, ces énoncés deviennent un théorème trivial, une très banale conséquence de cette définition.

Pour la même raison, on peut maintenant définir avec grande exactitude la notion d'existence, sur la base de cet Univers ou sur la base du mot clef chose. Exister, c'est par définition "être un élément de l'Univers TOTAL", c'est-à-dire "être un élément de l'Ensemble de toutes les choses"; donc exister, c'est tout simplement "être une chose".

• Fractale, Structure fractale

On dit qu'une chose A est fractale (adjectif masculin "fractal"), une fractale (nom féminin), ou a une structure fractale, s'il existe au moins un élément (ou une partie) B de A qui est une reproduction parfaite de A, un petit modèle de A. Comme B est un petit modèle de A, il en résulte B a à son tour une structure fractale comme A, B possède de la même manière une partie C qui est son petit modèle, et qui possède de la même manière un petit modèle D, etc.

Une structure fractale se reproduit donc identiquement à elle-même à toutes les échelles :

Triangle de Sierpinski, un exemple de structure fractale.
On peut très facilement identifier des triangles intérieurs, plus ou moins petits,
qui reproduisent exactement le même modèle que le triangle total.

L'Univers TOTAL est la plus grande de toutes les structures fractales, du fait de sa propriété d'Auto-appartenance.

• Infini, Zéro

"D'une manière très générale, une chose X est dite infinie, si X est égal à au moins une autre chose Y, qui est différent de X. Et en particulier, un ensemble X est dit infini s'il reste lui-même, qu'on lui ajoute ou qu'on lui retranche un élément."

Voilà une définition pour le moins très inhabituelle de la notion d'Infini, et pourtant, c'est la plus simple, la plus générale, la plus universelle, la plus puissante ! Derrière cette description se cache tout simplement l'Univers TOTAL, l'Infini lui-même ! Intuitivement, ajouter 1 ou retrancher 1 à l'Infini, il reste toujours l'Infini. Si on l'appelle X, il est donc lui-même et lui-même plus 1, donc on a : X = X + 1; et il est lui-même et lui-même moins 1, donc on a : X = X - 1.

Si un ensemble ou une chose est au GRAND COMPLET, vous ne l'augmentez pas d'un iota en ajoutant une chose supplémentaire, sinon l'ensemble n'était pas vraiment COMPLET. Cela signifie que tout ce que vous pouvez lui ajouter était déjà dans l'ensemble, même s'il a un air de Vide (voir Anti-Univers) !

De même, vous ne diminuez pas cet ensemble ou cette chose en lui retranchant un élément, car l'élément enlevé se trouve toujours quelque part au fin fond de ce qui reste. Vous n'augmentez donc et ne diminuez cette chose infinie que relativement parlant, et pas dans l'absolu, sinon elle n'est pas infinie, elle n'est pas complète, elle n'est pas TOTALE. Cette définition de l'Infini n'esr qu'une autre façon d'exprimer la Loi d'Auto-appartenance de l'Univers TOTAL (voir Auto-appartenance). Mais c'est aussi une autre manière d'exprimer sa structure fractale : "Le tout est identique à n'importe laquelle de ses parties".

Les notions de Zéro et d'Infini (ou Fini et Infini) sont parmi les notions les plus mal conçues actuellement, de même que la notion de Variable (ou le couple Constante, Variable), alors que les deux ne sont que deux formes d'une seule et même notion. Le mot "infini" est actuellement utilisé pour désigner des notions très différentes. Par exemple, en mathématiques, le mot "infini" n'a pas du tout le même sens dans les deux phrases suivantes : "Le rapport 1/X tend vers l'infini quand X tend vers 0" et : "L'ensemble des entiers naturels N = {0, 1, 2, 3, 4, 5, 6, 7, ...} est un ensemble infini".

Dans ces phrases, on parle, en principe, de deux notions d'infini complètement différentes. La première est très associée à l'idée qu'il existe toujours un nombre X plus petit que tout nombre strictement positif que l'on peut se fixer à l'avance. C'est ce qu'on entend par "X tend vers 0". Et l'inverse, c'est qu'il existe toujours un nombre X plus grand que tout nombre strictement positif que l'on peut se donner à l'avance. C'est ce qu'on entend par "X tend vers l'infini". Cela revient à dire simplement que, tout en restant strictement positif, le nombre représenté par la variable X est toujours plus petit ou plus grand que toute valeur qu'il avait auparavant. Autrement dit encore, X est aussi petit que l'on veut, et aussi grand que l'on veut, tout en restant toujours strictement positif. Cette notion d'Infini est étroitement liée à la notion de Variable.

Mais la seconde idée, celle qui dit que l'ensemble des entiers naturels N est infini, veut simplement dire qu'il existe une partie de N, qui n'est pas N tout entier, mais qui pourtant a le même nombre d'éléments que N. Autrement dit, plus simplement, N est un genre d'ensemble dont le nombre d'élements de change pas, qu'on lui ajoute un élément ou qu'on lui enlève un élément ! Si nous appelons par exemple X le nombre des éléments de N, on a : X = X + 1, et X = X - 1. Si on calcule normalement avec un tel nombre, on aboutit à l'étrange conclusion : 0 = 1, dont la science actuelle a une horreur, et qui pourtant est la définition même de l'Infini, mais aussi de la notion de Variable !

Et aussi, il y a autant de nombres pairs (qui sont donc au nombre X/2) que de nombres entiers au total (qui sont au nombre total de X) ! On a donc : X = X/2 ou X = 2X. Une telle égalité, si on calcule normalement avec elle, aboutit à l'étrange conclusion que : X = 0 ! C'est totalement inacceptable dans la logique actuelle (la Logique Négative), car cette logique interprète ce résultat comme signifiant : "Le nombre total des élements de l'ensemble N entiers naturels est 0", ou "Il n'existe aucun entier naturel" !

Mais il s'agit d'une très mauvaise interprétation due au fait que l'on fait pas la science avec l'Univers TOTAL, et donc on ne peut pas comprendre ce que de telles égalités 0 = 1 ou 0 = X veulent dire. Elles signifient simplement simplement que le premier nombre ou premier ordinal (l'Alpha) est aussi le dernier nombre ou dernier ordinal (l'Oméga). Autrement dit, quand on a atteint le plus grand de tous les infinis, l'Infini (avec I majuscule), alors on aura bouclé le grand Cycle des nombres, et on revient à la case départ, au premier des nombres, à savoir 0. C'est simplement comme le fait de partir d'un point O ou 0 d'une piste circulaire pour faire un tour de piste, ou de partir d'un point de l'Equateur et de vouloir faire un tour du globe. Tant qu'on n'a pas bouclé le grand tour, on est un point différent du départ, de O, de 0, et on a à chaque instant l'impression que la trajectoire est droite, ou que la terre est plate, d'autant plus si le Cycle est grand, très grand ! Mais si on le boucle, alors on se retrouve au point O ou 0.

C'est tout simplement une loi de l'Univers TOTAL, l'Infini lui-même. C'est avec lui que l'on découvre les secrets les plus cachés du Zéro et de l'Infini, de l'Alpha et de l'Oméga, qui sont donc deux faces contraires d'une seule et même chose. Et aussi, on découvre avec étonnement que la notion d'Infini et de Variable sont dans l'absolu la seule et même notion, appartenant à la Famille ENSEMBLE, et donc aussi que leurs contraires respectifs Zéro et Constante sont la même notion, appartenant à la Famille ELEMENT.

La notion d'Infini X, tout comme celle de Variable X, peut se définit par cette égalité : 0 = 1, la manière la plus simple de dire : X = X + 1. Une autre manière de définir l'Infini X ou la Variable X est l'égalité : X = 0 ou 0 = X, une simple manière de dire : X = X + X, c'est-à-dire de parler du nombre qui ajouté à lui-même donne lui-même, ou du nombre qui est son propre double. 0 est le premier nombre qui vérifie cette loi : 0 = 0 + 0, mais l'Infini aussi la vérifie : Infini = Infini + Infini, et pour cause : les deux sont deux faces de la même chose.

M-Z

• Négatif (1)

Adjectif de Négation (1); comme dans "phrase négative" ("Il ne pleut pas") ou dans "nombre négatif" ("-5"). C'est la notion de négatif dans toute sa généralité, donc la notion normale. Dans ce cas-là, la Science Nouvelle préfère parler de Contraire, d'Antipode ou utliser le préfixe Anti, pour bien distinguer de Négatif (2) et et de la Négation (2), qui sont des cas extrêmes de négation.

• Négatif (2)

Adjectif de Négation (2); synonyme de Mauvais ou Mal; opposé à Alternatif ou Positif (2) ou Bon ou Bien. Il s'agit d'un cas particulier et extrême de Négatif (1), le cas absolu.

• Négation (1)

Nier au bon sens du terme (le sens alternatif), signifie alterner, c'est-à-dire "faire le choix du contraire d'une chose" ou "affirmer le contraire d'une chose" (voir Affirmation et Négation). C'est la negation au sens très général du terme, la négation relative, puisque, contrairement à la négation absolue (la Négation (2)), elle ne signifie pas par exemple le fait d'affirmer le contraire d'une réalité ou d'une vérité, mais simplement le fait d'affirmer le contraire d'une chose. Celui qui affirme simplement le contraire d'une chose peut être celui qui dit la vérité, si la chose en question se trouve ne pas être vraie (pour plus de détails, voir Négation (2)).

• Négation (2)

Nier au mauvais sens du terme, "c'est refuser à une chose une qualité ou un attribut qu'elle possède, en particulier la qualité de chose, d'existence, de vérité, de réalité, de possibilité, etc.; c'est dire par exemple qu'elle n'existe pas alors qu'elle existe, qu'elle n'est pas vraie alors qu'elle est vraie, qu'elle n'est pas réelle, alors qu'elle est réelle, qu'elle n'est pas possible alors qu'elle est possible, etc." C'est le sens négationniste de la Négation.

Nier au mauvais sens du terme, "c'est attribuer à une chose une qualité qu'elle ne possède pas." C'est le sens mensonger ou de tromperie de la Négation.

Et nier au mauvais sens du terme, "supprimer chez une chose une qualité ou un attribut qu'elle doit posséder." En ce sens, un meurtre (ôter la vie à une personne qui ne mérite pas la mort) est un acte de Négation.

Cette négation est absolue, c'est le cas extrême de Négation (1), mauvaise pour celle raison-là. Celle-ci ne signifie pas par exemple le fait d'affirmer le contraire d'une réalité ou d'une vérité, mais simplement le fait d'affirmer le contraire d'une chose. Celui qui affirme le contraire d'une chose peut être celui qui dit la vérité, si la chose en question n'est pas la vérité.

Si par exemple l'un dit : "Il pleut" et que l'autre dise : "Il ne pleut pas", il dit le contraire de la première chose, il la nie donc, et peut être celui qui dit la vérité, si effectivement il ne pleut pas. Ici, la discusion porte sur la phrase "Il pleut" dans un contexte donné et non pas dans l'Absolu, car dans les deux phrases sont vraies, et les deux ont donc raison dans l'Absolu. Par conséquent, celui qui nie cette vérité uniquement dans ce contexte est coupable seulement d'un petit mensonge, un mensonge limité à un contexte, et l'Absolu le rachète, si toutefois par "Il pleut" il avait à l'esprit cette vérité dans l'Absolu.

Mais la question est autre si les phrases contraires étaient : "Les deux phrases 'Il pleut' et 'Il ne pleut pas' ne peuvent jamais être vraies toutes les deux à la fois" et "Les deux phrases 'Il pleut' et 'Il ne pleut pas' peuvent être vraies toutes les deux à la fois". Là, la discussion porte sur une vérité absolue, qui est la seconde déclaration. Par conséquent, c'est le premier qui affirme le contraire de cette vérité, qui la nie, et sa négation est tout simplement absolue, sans autre forme de procès.

De même, si l'un dit : "L'égalité '0 = 1' n'est pas une vérité scientifique" et que l'autre le contredise (c'est-à-dire affirme le contraire) en disant "L'égalité '0 = 1' est une vérité scientifique", c'est lui qui dit la vérité (même si elle a l'air d'une fausseté), car effecivement "L'égalité '0 = 1' est une vérité scientifique" au même titre que de dire "L'énoncé '0 est différent de 1' est une vérité scientifique." Autrement dit, "la diffférence entre 0 et 1" ainsi que "l'égalité entre 0 et 1" sont tous les deux des réalités dans l'Univers TOTAL, ce sont deux vérités dans l'Absolu.

C'est la différence entre la négation relative (Négation (1)) et la négation absolue. Toute négation absolue revient toujours à nier l'Univers TOTAL, la plus grande de toutes les réalités. L'existence de cet Univers est remise en question dès lors que l'on refuse une vérité absolue. Quand nous employerons le mot Négation sans autre précision, cela signifiera le plus souvent cette négation absolue, cette négation extrême, qui est synonyme de Mauvais pour toutes les raisons présentées. Elle et l'Alternation sont tout le contraire l'une de l'autre. On a : Négation = Anti-Alternation = U - Alternation = -Alternation; et donc : Alternation = Anti-Négation = U - Négation = -Négation, où U désigne l'Univers TOTAL (pour la signification de ces opérations, voir à Contraire).

Nom (ou Mot ou Symbole) et Sens (ou Signification)

On appelle Nom ou Mot, une chose quelconque A dont la fonction est de désigner ou de représenter une autre chose quelconque B. La chose A est appelée un "Nom propre" si B doit être vu comme une seule chose, comme un seul élément de l'Univers; dans ce cas, A est aussi appelé une Constante. Et A est appelé un "Nom commun" si B doit être considéré comme un ensemble; A est alors appelé une Variable, un Nom commun à tous les éléments de B. Dans tous les cas, on dit que A est un Nom, un Mot, un Symbole, qui désigne, représente ou symbolise B. Et B est appelé le Sens ou la Signification de A. Et on note simplement : A = B.

Par exemple, je peux avoir dans la main gauche un caillou et dans la main droite une fleur, et décider que le caillou n'est pas à considérer en lui-même, mais comme désigant ou représentant ou symbolisant la fleur. Quand je dis alors "caillou", il faut comprendre "fleur", donc que je parle de la fleur. Et on écrira : caillou = fleur. Et je peux au contraire décider que caillou représente l'ensemble des villes : {Sydney, Paris, Rome, Lomé, Ouagadougou}. Et alors caillou est un nom commun pour ces villes, et on écrira aussi : caillou = {Sydney, Paris, Rome, Lomé, Ouagadougou}.

Dans une science qui ne repose pas sur l'Univers TOTAL, un Nom, un Mot ou un Symbole n'est qu'une simple étiquette que l'on "colle" sur une chose donnée, pour la distinguer des autres choses. C'est ainsi par : caillou = fleur, on comprendra seulement que je me sers du caillou comme une simple étiquette pour la fleur, et qu'il ne faut pas du tout comprendre par là qu'un caillou est la même chose qu'une fleur !

Mais dans une science qui repose sur l'Univers TOTAL, un Nom, un Mot ou un Symbole n'est pas qu'une simple étiquette, et qu'une égalité comme : caillou = fleur, veut dire aussi, eh bien ce qu'elle veut dire ! L'Univers TOTAL en effet obéit à des lois extraordinaires comme la loi d'Auto-appartenance, et il possède une structure fractale : "La partie (ou l'élément) est la même chose que le tout !" Autrement dit, l'Univers TOTAL est chacun de ses éléments, et donc en particulier le caillou et la fleur ! De ce fait, deux éléments quelconque A et B ou X et Y, comme par exemple caillou et fleur, malgré toutes les différences apparentes, ne sont finalement que deux manières différentes de parler du seul et même l'Univers TOTAL, un Univers Fractal. Sachant cela donc, l'égalité caillou = fleur prend toute une autre importance !

Oméga

Terme général qui regroupe tous les mots synonymes de "Univers": Plein, Tout, Infini, Espace, Cosmos, etc.

En un sens plus particulier, comme nombre (ou ordinal), il désigne l'Infini, le dernier ordinal (le nombre nombre), et plus exactement l'Ensemble Plein (ou simplement Plein), à savoir l'Ensemble de tous les ensembles, c'est-à-dire donc une simple autre façon de parler de l'Ensemble de toutes les choses, l'Univers TOTAL. Il est inconnu dans les sciences actuelles, il est même simplement banni, car accusé de paradoxe, en l'occurrence le Paradoxe de Burali-Forti (voir le Paradoxe Universel).

Parce qu'elle repose sur l'Univers TOTAL, la Science Noucelle réhabilite tout simplement l'Ensemble de tous les ensembles, l'Ensemble Plein, Oméga donc. Il est noté : 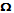, et son contraire est Alpha.

• Particule

Dans la physique actuelle (plus précisément en physique des particules), on emploie le mot "particule" pour désigner des objets matériels dits "infiniment petits", et concrètement qui sont à des échelles inférieures à celle de l'atome. Par exemple, l'atome d'Hydrogène (H), est un constitué seulement de deux particules, un proton et un électron. Mais, en général, cet ensemble n'est pas lui-même appelé une particule, car avec lui commence le monde des atomes, puis des molécules, puis des choses de plus en plus grandes comme les cellules, les organes, etc. Par contre, le noyau de l'atome d'Helium (He²⁺), qui lui est constitué de 2 protons et de 2 neutrons, qui est donc environ 4 fois plus "gros" qu'un atome d'Hydrogène (puisque la taille d'un électron est très petite par rapport à celle d'un proton, qui, lui, est du même ordre de grandeur que le neutron), est appelé une particule, en l'occurrence la "particule alpha".

Ces conceptions (comme beaucoup actuellement) manquent donc cruellement de précision. Cela reste très arbitraire, comme d'ailleurs aussi est arbitraire la prétendue séparation entre l'infiniment petit et l'infiniment grand. Tout est en fait comparé à notre échelle, l'échelle ordinaire, l'échelle 0 (voir Contexte, Echelle). On raisonne comme si ces notions d'infiniment petit et d'infiniment grand sont absolues, alors qu'elles sont très relatives ! Tout simplement comme en général les notions de "petit" et de "grand". Tout dépend à quoi une certaine chose est comparée. Un proton comparé à un photon, à un neutrino (et même à un électron), est "infiniment grand"; mais le même proton est "infiniment petit" comparé à un caillou ou à une bille avec laquelle un gamin joue.

C'est donc actuellement une très grossière erreur qui consiste à séparer la physique en deux : la physique de l'infiniment grand (comme par exemple la théorie de la relativité) et la physique de l'infiniment petit (par exemple la physique des particules ou la mécanique quantique), les deux physiques obéissant à des paradigmes et à des lois de natures très différentes, réputées difficiles à concilier. Mais l'erreur vient de ce que la science n'est pas fondée sur l'Univers TOTAL, et donc on ignore actuellement ses lois comme l'Auto-appartenance, qui dit par exemple que cet Univers tout entier est un élément d'une autre version de lui-même, par rapport à qui il est une particule (voir Anti-Univers) !

En conséquence, les choses sont beaucoup plus simples et précises dans la Science Nouvelle. Au sens le plus large du terme, une particule, c'est tout simplement... n'importe quelle chose ! Une chose donnée est toujours infiniment petite (donc une particule) comparée à une autre, qui est donc infiniment grande comparée à elle. L'Anti-Univers, noté O et appelé aussi le Zéro ou l'Alpha, est la plus petite de toutes les particules, la "Particule Alpha" ou simplement "Particule", à ne pas confondre avec la "particule alpha", le noyau de l'atome d'Helium (He²⁺).

La nouvelle conception de la notion de particule permet de faire la physique des particules (ou la physique quantique) la plus générale et la plus universelle qui soit, qui englobe l'infiniment petit et l'infiniment grand dans une seule Physique (la Physique de toutes les choses), dans une seule Science.

• Positif (1)

Comme dans "nombre positif" comme +5. Synonyme de Affirmatif; opposé à Négatif (1).

• Positif (2)

Synonyme de Bon, de Bien; opposé à Négatif (2).

• Quantum, Quanta, Quantique

"Un quantum (au pluriel quanta) la plus petite unité d'un ensemble donné, ou ce que l'on décide de considérer comme la plus petite unité, qui sert à compter les éléments de l'ensemble, à indiquer leur quantité, leur nombre, sous forme d'un nombre entier naturel : 0, 1, 2, 3, 4, 5, .... On dit alors dans ce cas que cet ensemble est divis, discret, quantifié. Dans le cas contraire, il est dit indivis, continu, qualifié."

Par exemple, le sable d'une plage est un ensemble, et le grain de sable est le quantum du sable, et les grains de sable sont les quanta du sable. On peut donc compter le sable sur la base de son unité (ou quantum) qu'est le grain, en disant : 0 grain, 1 grain, 2 grains, 3 grains, etc.

De même, l'eau d'un lac est un ensemble, et une molécule d'eau (de formule H₂O) est la plus petite unité de l'eau, son quantum, et les molécules d'eau sont les quanta de l'eau. On peut sur la base des molécules compter l'eau en disant : 0 molécule, 1 molécule, 2 molécules, 3 molécules, etc.

"Au sens le plus large du terme, un quantum est tout simplement un nom commun, comme par exemple : électron, proton, fruit, humain, etc. Ce nom commun exprime une qualité, une proriété commune à plusieurs choses, un attribut qui leur est commun, et sur la base duquel ces choses sont parfaitement égales, et comptées comme des unités égales, par exemple : 0 électron, 1 électron, 2 électrons, 3 électrons, etc., ou : 0 humain, 1 humain, 2 humains, 3 humains, etc."

Sur la base du mot électron donc, deux électrons sont égaux, quelles que soient les différences qu'ils peuvent avoir par ailleurs. De même, sur la base du mot humain, deux humains sont égaux et valent la même unité, même si l'un est grand et l'autre un bébé, et même si l'un est blanc et l'autre est noir. Si on veut les différencier, alors il faut former un autre quantum, comme par exemple "humain grand", "humain petit", "humain blanc", "humain noir". Sur la base de chacun de ces nouveau quanta, les choses comptées sont égales, chacune constitue une unité, égale à toute autre chose ayant cette qualité. Et si on veut différencier les deux unités, on affine encore une fois le quantum, etc.

Le quantum absolu est défini par le mot chose, c'est l'unité absolue, celle de l'Univers TOTAL. Sur la base de cette qualité, deux choses quelconques X et Y, quelles que soient leur différence par ailleurs, sont égales ! Sur la base de ce quantum, on compte l'Univers en disant : 0 chose, 1 chose, 2 choses, 3 choses, etc. Et on peut parler de la quantité ou du nombre de choses qu'il y a dans l'Univers TOTAL. Sur la base de ce quantum, on peut faire la physique quantique la plus générale et universelle qui soit, la Physique de toutes les choses.

• Univers (TOTAL), Existence, Plein, Tout, Infini, Espace, Cosmos, Oméga

Tous ces termes sont synonyme. Ils désignent l'Univers TOTAL, l'Ensemble de toutes les choses, le Tout, l'Absolu. Ils sont respectivement contraires de : Anti-Univers, Néant, Vide, Rien, Zéro, Point, Particule, Alpha (voir Anti-Univers).

D'une manière très générale, tout ensemble (quel qu'il soit) est appelé un univers, un tout, un plein, un espace, etc., car c'est ce qu'il est. Toutes les choses qui le constituent (ses éléments donc) sont les choses de cet univers.

Normalement, quand on dit "L'Univers" avec l'article "LE" et avec un "U majuscule", on ne devrait pas avoir à préciser qu'il est TOTAL, puisque le mot "Univers" à lui seul signifie déja "LE Tout" ou "Tout". Mais il se fait que l'Univers tel qu'on le conçoit pas actuellement n'est pas le Tout au sens le plus Absolu du terme, c'est-à-dire on ne parle pas de l'Ensemble de toutes les choses, d'où la nécessité de cette précision.

• Variable, Constante

"Une variable X, c'est par définition tout simplement une chose qui change, qui est tour à tour différentes choses, mais tout en restant elle-même, à savoir X. Et en un sens plus particulier, on dit qu'un nombre X est une variable s'il vérifie cette égalité : X = X + 1."

Cette "étrange" et puissante propriété, est tout simplement celle de l'Univers TOTAL, c'est lui qui se cache derrière cette description.

La notion de Variable est actuellement l'une des notions scientifiques les plus nébulleuses, tout comme exactement aussi la notion d'Infini, parce que mal conçues. C'est avec l'Univers TOTAL que ces deux notions livrent tout leur sens, tous leurs secrets et toute leur puissance. Car justement, cet Univers est l'Infini lui-même, la Variable elle-même. Et le contraire de cet Univers, l'Anti-Univers, le O, est le Zéro lui-même, la Constante elle-même.

Actuellement, la notion de "variable", très utilisée et très vitale en mathématiques, est en fait une notion métamathématique, c'est-à-dire une notion en dehors des mathématiques proprement dites, mais très utiles pour faire les activités mathématiques. Cela consiste à prendre par exemple les lettres de l'alphabet, pour représenter plus ou moins provisoirement des objets mathématiques proprement dits (des nombres par exemple), pour formuler des proriétés générales, etc. Les objets représentés sont les constantes ou les valeurs de la variable. Quand on représente une variable par une de ses valeurs, on se retrouve avec une expression qui ne concerne que des constantes.

La star des variables est la lettre X, utilisée pour écrire par exemple : F(X) = X + 1, ou : G(X) = X² + 3X -5. On fera par exemple : X = 0, ce qui donne : F(0) = 0 + 1 = 1, et : G(0) = 0² + 3x0 -5 = -5. Puis le coup d'après, on peut faire : X = 1, ce qui donne : F(1) = 1 + 1 = 2, et : G(1) = 1² + 3x1 -5 = -1. Etc.

La notion de variable X ainsi utilisée n'aura été qu'une notion abstraite pratique pour faire des calculs de ce genre, pour résoudre des équations qui peuvent être très complexes et très difficiles, comme par exemple les équantions de la rélativité ou de la mécanique quantique.

Mais dans ces manipulations, quelque chose de fondamental et de très élémentaire aura échappé à tous : la nature profonde de l'objet que l'on manipule ainsi que l'on appelle "variable". Quand on fait ce genre de manipulations, cela signifie que l'on doit accepter la chose fondamentale qui donne le droit de faire cela, l'Univers TOTAL. Sinon, toutes les activités avec les variables reposent sur de très subtiles paradoxes qui échappent à tous, d'autant plus si l'on nie par ailleurs cet l'Univers TOTAL (voir Oméga) ! Voici quelques exemples de choses qui échappent :

Par exemple, X est une variable, donc par définition une non-constante. Et 0 est une constante, et par définition une non-variable. Ce sont deux choses différentes donc, contraires même ! C'est la raison pour laquelle, actuellement, on a le droit d'écrire une chose comme : X = Y, car il s'agit d'une égalité entre deux variables différentes. Mais dans ces conceptions, sous-peine de contradiction, on n'a pas le droit d'écrire une choses comme : 0 = 1, qui est une égalité entre deux constantes différentes. C'est donc la preuve que variable et constante, ce n'est pas du tout la même chose.

Dans les conceptions actuelles, sous-peine de contradiction, on n'a pas le droit d'écrire une égalité entre deux choses différentes (et à plus forte raison contraires !) puisque l'égalité entre deux choses signifie qu'on parle finalement de la même chose. On n'a normalement donc pas le droit d'écrire des choses comme : X = 0 et X = 1, qui sont des égalités entre une variable et une constante, ce qui signifie que finalement X est aussi une constante et 0 et 1 sont aussi des variables !

Et de plus, la transitivité de l'égalité oblige que deux choses A et B égales à une troisième C, sont égales entre elles. Autrement dit, si on a : C = A et B = A, alors A = B. C'est dans cette situation que met obligatoirement l'usage de la chose étrange nommée variable, puisqu'une variable consiste simplement à utiliser une certaine même chose X pour écrire une série d'égalités avec des choses différentes, qui sont les valeurs que la variable peut prendre, par exemple : X = 0, X = 1. C'est l'intérêt même de la notion de variable, c'est ce qui fait en réalité toute la puissance de cette chose, et le secret de cette puissance est tout simplement l'égalité : 0 = 1 ! Qui dit : X = 0, X = 1, dit obligatoirement : 0 = 1, puisque 0 et 1 sont égaux à une troisième chose, qui est la variable X. C'est dans cette égalité que se trouve la définition même de la notion de Variable, mais aussi de l'Infini.

En effet, c'est parce que cette étrange chose X nommée Variable est aussi l'étrange chose X nommée l'Infini, que l'on a le droit d'écrire : X = 0, une étrange égalité entre un variable et une constante. Si on restait vraiment fidèle à la Logique Négative actuelle, on n'aurait pas le droit d'écrire : X = 0, mais aussi de dire : X = 0 et X = 1, sans dire 0 = 1 ! Officiellement donc, la science actuelle rejette une telle égalité qualifiée d'absurde. Mais officieusement, elle utilise bel et bien cette dite "absurdité", car sans elle la science ne peut pas aller bien loin.