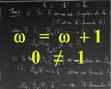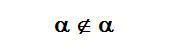Thèse pour l'université

Le nouveau paradigme Syn-Thèse pour l'université Voir aussi : Le Principe d'Alternation Logique mathématique de Jussieu et IHES Théorie universelle des ensembles Théorie des univers Hubertelie au Maître de Conférence La Faculté de la Science Vite dit en vidéos 12 1) Toute la Lumière sur les Paradoxes 2) L'Algèbre du Cycle Le nouveau paradigme Deux logiques, deux sciences « Il est impossible qu’un même attribut appartienne et n’appartienne pas en même temps et sous le même rapport à une même chose » (Aristote, Métaphysique, 1005 b 19-20). C'est ainsi qu'Aristote (384 - 322 av. JC) a formulé le principe de non-contradiction (article Wikipedia), fondamental dans le raisonnement scientifique actuel. La question du Théorème de l'Existence est avant tout et après tout une question de paradigme. Il y a d'une part la science qui ne repose QUE sur le principe de non-contradiction, sur une manière de raisonner et sur une conception de la vérité qu'on peut qualifier d'aristotélicienne (je dis plus simplement aristotélienne...); et il y a la science qui repose le principe d'alternation, un principe universel, dont le principe de non-contradiction n'est qu'un cas particulier, un cas limite ou canonique. Le principe d'alternation fonde une logique absolue, qui est la manière absolue raisonner et de concevoir la vérité. Il peut s'énoncer ainsi : "Le contraire de toute vérité est toujours une autre vérité", ou simplement : "Tout est vrai". A comprendre par là qu'il existe toujours un contexte où ce qui était impossible (ou faux) dans un certain contexte devient possible (ou vrai). Et dans un même contexte donné, ce qui était impossible en absordant les choses d'une certaine façon devient possible en les abordant autrement. Ou ce qui était faux pour une chose dans ce contexte devient possible pour une autre version de la même chose dans ce contexte. Bref, ce qui est faux d'un certain point de vue est toujours possible d'un autre point de vue. Le mot "autre" (ou "alter" en latin) est vital dans ce concept d'alternation, et c'est aussi le mot dans "altener", "alternance" ou "alternatif", comme dans "courant alternatif". La notion de symétrie ou d'égalité par permutation des rôles est cruciale, pour qu'on puisse dire par exemple qu'on a une "autre version de la même chose", concept fondamental dans la notion d'alternation. De ce point de vue, les nombres (+3) et (-3) sont deux versions différentes de la même chose, ils sont égaux au signe près, et il suffit de changer (ou d'alterner) le sens choisi comme positif, pour que (+3) devienne (-3) et vice-versa. Et dans le schéma ci-dessus montrant une courbe alternative, le sommet (ou "sommet de la vague") et le creux (ou "creux de la vague") sont deux versions différentes de la même chose, au sens de l'alternation, car ils jouent un rôle parfaitement symétrique. Et de ce point de vue aussi, les côtés "recto" et "verso" d'une feuille sont, par alternation, deux versions de la même chose, car n'importe lequel peut être appelé "recto", et alors l'autre s'appelle le "recto"; mais en inversant (ou en alternant) les appellations, ça marche aussi ! Comme le montrent les schémas ci-dessus, le courant continu est un cas particulier de courant alternatif, le cas de fréquence 0 et de période infinie; c'est donc un cas extrême, un cas limite, le cas stationnaire, le cas canonique, qui permet de qualifier les autres de variables. La notion de courant alternatif (et plus généralement de courant variable) est donc plus riche et plus féconde que celle de courant continu. Exactement de la même façon, le repos est un cas particulier et limite de mouvement, le cas de référence qui permet justement de qualifier les autres de "mouvement" à proprement parler. C'est exactement ce que la logique aristotélienne est pour la logique hubertélienne, un simple cas limite (mais important), à partir duquel la logique commence dans toute sa puissance ! Un exemple historique vérifiant le principe d'alternation La logique aristotélienne est aussi pour la logique hubertélienne, ce que la géométrie euclidienne est pour la géométrie dans son ensemble. Pour sa géométrie, Euclide a posé ses postulats, dont le fameux cinquième postulat (ou axiome) qui dit que "Par un point extérieur à une droite il passe une droite et une seule parallèle à la première". Et on sait qu'on peut tout à fait avoir une géométrie dans laquelle par exemple c'est le contraire de ce postulat (ou axiome) qui est vrai. Cet exemple historique de la géométrie euclidienne est de grande importance dans la philosophie des sciences; c'est aussi un cas important illustrant le concept d'alternation : "Le contraire de toute vérité est toujours une autre vérité" ou "Tout est vrai". Ce programme n'est que partiellement rempli par la méthode axiomatique, car le fameux principe de non-contradiction le limite et lui interdit d'être tout simplement la vérité universelle, la vérité absolue, pour une science vraiment universelle et absolue. Ce postulat et son contraire sont simplement deux versions de la même chose, au sens de l'alternation; ils sont deux faces différentes de la même vérité, exactement comme (+3) et (-3), comme le sommet et le creux d'un courbe alternative, ou comme les côtés recto et verso d'une même feuille. Dans l'absolu, l'un n'est pas plus vrai ou plus faux que l'autre. C'est ainsi que l'on devrait considérer en général tout énoncé A quel qu'il soit !, et son contraire (ou sa négation), à savoir non-A. Mais bien que constatant la réalité de l'alternation dans des cas particuliers, la pensée actuelle se refuse à en faire une généralité, une vérité universelle, l'énoncé même de la vérité absolue. L'alternation bridée par une conception étriquée de l'égalité Voyons brièvement comment le principe d'alternation s'illustre aussi dans l'histoire des nombres. En arithmétique et en algèbre des corps, les nombres entiers naturels jouent le même rôle que la géométrie euclidienne. Ce qui n'est pas vrai dans un cadre, le devient dans un autre cadre plus large. Par exemple, il est impossible de trouver un nombre entier naturel x tel que : x + 5 = 2. C'est le nombre entier relatif (-3) qui répond à ce signalement; mais on ne connaît pas de nombres négatifs dans les entiers naturels, à moins justement de fonctionner dans la logique alternative, la logique hubertélienne... Alors dans ce cas on sait simplement que (-3) n'est qu'une autre façon de dire (+3). Donc, sous une autre forme et d'un autre point de vue, il existe bel et bien un entier naturel tel que : x + 5 = 2. Non seulement cela, on sait aussi que même (+3) est carrément lui aussi une solution, de même que (+4), (+5), (+6), bref, tout entier naturel ! En effet, dans la logique huberteliénne, on a par exemple : 4 + 5 = 2, c'est-à-dire donc : 9 = 2 ! Erreur ? Etrange ? Oui, si on ignore la réalité qu'est le Cycle. L'égalité 9 = 2 ou 2 = 9 (donc 0 = 7) n'est que l'écriture du cycle 7 dans cette logique, cycle dont la définition est 0 = 7. C'est par exemple le cycle de la semaine. Si la fin d'un mois est mercredi, le 7 du mois suivant est un mercredi, et les dates 14, 21, 28 du mois sont aussi des mercredis. Ce cycle permet de dire que "ces dates sont même jour de la semaine". Et le 2 du mois ainsi que le 9 sont aussi le "même jour de la semaine", de même que le 16, etc. L'équivalence est une notion très puissante qui permet de découvrir les facteurs d'égalité ou de similitude entre les choses différentes, de détecter les choses semblables, les choses obéissant à un certain même modèle, etc. C'est donc une notion d'égalité plus générale donc plus puissante que celle qui consiste à ne dire que 0 = 0, 2 = 2, 7 = 7, 9 = 9, 14 = 14, bref A = A ou N = N, égalité au sens restreint du terme, qui n'est que l'expression du cycle 0, un cas limite donc, exactement comme un courant continu est un cas limite du courant alternatif, le cas de fréquence 0. En fait "cycle 0" ou "fréquence 0", ce sont que des manières différentes d'exprimer la même chose. D'une manière générale, le cycle N (que j'aurais appeler aussi "fréquence N") est défini par l'égalité : 0 = N, et le raisonnement et les calculs avec le cycle s'apparente à ce qu'on appelle actuellement les calculs de congruence. L'écriture 0 = N sera donc actuellement interprétée comme la congruence modulo N. Dans cette congruence, k et k + N sont congruents, c'est-à-dire sont égaux à N près ou égaux modulo N. Dans la logique du cycle (c'est-à-dire donc dans l'alternation), n'importe quel entier naturel est solution de l'équation : x + 5 = 2, là où il était impossible avec la logique aristotélienne de trouver un seul ! Par exemple, 30 est aussi solution, car 30 + 5 = 2, ou 35 = 2, une égalité du cycle 33. Sans la notion de cycle, dire cela c'est dire "nimporte quoi", tout comme dire 0 = 1 ou 7 = 40000. Mais c'est "n'importe quoi" si on ne voit pas la logique qui peut se cacher dans le fait d'écrire une égalité entre deux choses différentes A et B. Mais ce n'est plus "n'importe quoi" quand cette logique est celle du Cycle, et si de plus on connaît actuellement ce mode de raisonnement, comme par exemple la congruence. D'une manière plus générale, le langage du Cycle est simplement un langage de relation d'équivalence, SAUF (et là c'est très important !) que maintenant il s'agit du langage général de la science, et non pas seulement une situation particulière de la logique aristotélienne, comme c'est le cas actuellement. En effet, c'est l'égalité telle qu'elle est conçue actuellement qui est un cas pariculier de relation d'équivalence, et non pas le contraire ! On devrait plutôt parler de l'égalité en général, de la forme A= B (ou 0 = N), et qui a un cas particulier de la forme A = A (ou 0 = 0), est un cas trivial moins riche. Or c'est ce cas trivial qui est la conception générale de l'égalité dans la science actuelle, la notion d'équivalence (qui est très importante en physique aussi, comme par exemple dans l'équivalence masse-énergie) étant traitée comme un cas particulier. Ce faisant on met en fait la charrue devant les boeufs ! et alors la science ne peut que mal fonctionner, même si elle a l'air de bien fonctionner. Traiter l'équivalence dans le cadre restreint actuel de l'égalité, c'est vouloir loger un éléphant dans une boîte d'allumettes. C'est de là que viennent toutes les impossibilités de la science actuelle, car l'équivalence (le Cycle donc) y a du mal à exprimer sa pleine puissance ! L'alternation est donc actuellement bridée, car c'est avec l'équivalence (ou le cycle) qu'elle exprime sa pleine puissance. Les limites de la science actuelle Dans la logique aristotélienne (la logique classique),on peut définir un ensemble de nombre plus vaste (les nombres entiers relatifs) dans lequel l'équation x + 5 = 2 a maintenant une solution, (-3). Il faut préciser que c'est grâce justement au cas particulier d'alternation qu'est le cycle 0. Car, -3 + 5 = 2, donc 2 = 2, donc une égalité du cycle 0. Grâce à ce cycle trivial donc (le seul actuellement connu), ce qui était donc faux dans un contexte devient vrai dans un autre contexte. Le principe d'alternation se trouve alors vérifiée : "Le contraire de toute vérité est toujours une autre vérité". Dans la logique classique, la phrase "Il existe un entier naturel x tel que : x + 5 = 2" est tout bonnement fausse, sans autre forme de procès ! Or pourtant elle est bel et bien vraie, sans être forcément obligé de changer de contexte, mais en utilisant la puissance de l'alternation (ou du cycle). Mais pourquoi mobiliser une bombe atomique pour tuer une fourmi, là où un simple doigt suffit pour l'écraser ? La bombe atomique ou l'arme logique absolue qui fait se désintégrer tous les murs d'impossibilité, c'est ce qu'est le principe d'alternation. Si donc on a pu résoudre cette équation x +5 = 2 autrement, c'est parce que les ressources de la logique aristotélienne (donc du principe de non-contradiction) suffisent pour résoudre le problème, pour peu que l'on place dans le contexte adéquat. Il en est ainsi pour tous les problèmes qui se posent pour les nombres rationnels, réels, complexes, etc. qu'on peut actuellement résoudre. Par exemple l'équation : 3x + 4 = 0, insoluble dans les entiers relatifs, mais soluble dans les nombres rationnels. Ou l'équation x² + 1 = 0, insoluble dans les rationnels mais soluble dans les nombres complexes. A chaque fois, les ressources de la logique aristotélienne permettent de trouver un contexte où ce qui était faux dans un contexte devienne vrai dans un nouveau; et alors le principe d'alternation : "Le contraire de toute vérité est toujours une autre vérité", se trouve vérifié. Mais il est très facile aussi de trouver des problèmes insolubles avec la logique actuellement. Avec eux on a atteint les limites du possible avec la logique aristotélienne. Par exemple, on a vu il ne faut pas insister pour trouver un entier naturel qui vérifie : x + 5 = 2, ou un nombre rationnel qui vérifie : x² = 3, ou un nombre réel qui vérifie : x² = -1. Il faut changer de contexte numérique pour que cela soit possible, parce qu'on ne cherche les solutions que dans le seul cycle 0. Et maintenant, même en élargissant tous les contextes numériques précédents, les équations comme : x = x + 1 ou 0x = 1 sont impossibles. On ne peut leur trouver des solutions qu'au prix de l'abandon de propriétés vitales des nombres, ou alors c'est le principe de non-contradiction qu'il faut abandonner ! Par exemple, en appliquant les règles élémentaires du calcul algébrique, x = x + 1 conduit immédiatement à : 0 = 1, égalité du cycle 1, qui à elle seule signifie qu'on ne fait plus la science avec le principe de non-contradiction ! Et quand à 0x = 1, il demande simplement d'écrire : x = 1/0, donc de diviser par 0, ce que ce principe interdit. Pour les mêmes raisons, en théorie des ensembles, la phrase "Il existe un dernier ordinal" ne peut être vraie actuellement. Et quant aux phrases du genre : "Il existe d'autres univers", "La vie éternelle est possible", "La résurrection des morts est possible", "Les miracles de la Bible sont une réalité", "Le récit de la Genèse est vrai", "Adam et Eve ont existé", "Les anges existent", "Dieu existe", etc., on considère actuellement qu'avec elles on sort du domaine de ce qu'il faut appeler science ! Mais on ne sort pas de la science, mais on sort simplement de la science aristotélienne et des limites étroites fixées par son sacro-saint principe de non-contradiction (voir les documents comme L'anatomie de la Contradiction ou La logique des Shadoks).

Syn-Thèse pour l'université

De l'axiomatique à la théorématique

Le lecteur est invité à découvrir ici une petite synthèse d'un document de près de 250 pages nommé Thèse pour l'université, adressée en juillet 2006 à Monsieur Kokou Tchariè, maître de conférence et professeur de mathématiques à l'Université de Lomé au Togo. En partant des problèmes des fondements de la logique et des mathématiques, cette thèse revoit aussi les fondements de la physique, de la biologie, bref de l'ensemble des sciences. Ici nous nous limiterons essentiellement à la question des fondements de la logique et des mathématiques.

Le but de la Thèse pour l'université est de démontrer les lacunes intrinsèques du paradigme scientifique actuel, de combler ces lacunes, pour que la science puisse vraiment prétendre s'attaquer aux questions existentielles, à commencer par la question de la vie ! Une nouvelle méthodologie et voie d'approche scientifique est proposée, qui est la théorématique, complètement à l'opposé de l'actuelle axiomatique.

Le problème de l'Ensemble plein !

Depuis l'antiquité, on connaissait de nombreux paradoxes en logique et en mathématiques. Il y a par exemple le vieux Paradoxe du menteur. C'est le paradoxe d'une personne qui dit : "Je mens". La question est de savoir si la personne ment ou dit la vérité en prononçant précisement cette phrase. Si la phrase "Je mens" est un mensonge, alors la personne dit vrai. Et si elle dit vrai, alors c'est vrai qu'elle ment, donc elle ment, donc elle ne dit pas vrai. D'où le paradoxe, qui se résume par cette équivalence logique entre les valeurs de vérité VRAI et FAUX :

VRAI <=> FAUX.

La théorie des ensembles introduite par Georg Cantor en 1882 est la théorie fondamentales des mathématiques. Après son introduction, on découvrit divers paradoxes (question développée dans la vidéo 1 : Toute la Lumière sur les Paradoxes), ce qui déclencha ce qu'on appelle la crise des fondements de la logique et des mathématiques. Il y a par exemple le Paradoxe de Russell, qui est la question des ensembles qui n'appartiennent pas à eux-mêmes. Appelons de tels ensembles les alphas :

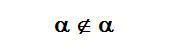
Et la question est de savoir s'il existe un ensemble dont les éléments sont exactement ces alphas. Si oui, alors appelons Alpha (ou A) un tel ensemble. On aurait tout aussi bien pu l'appler Oméga comme dans la vidéo, pour adopter la convention d'appellation uniforme dans tous les problèmes de paradoxe, qui impliquent en fait le seul et même grand ensemble, l'Ensemble plein (ou Ensemble de tous les ensembles). Alors la question est de savoir si A appartient ou non à lui-même. Autrement dit, A est-il ou non un de ces ensembles alphas qui sont précisément ses éléments.

Si on dit que A appartient à lui-même (donc s'il est un alpha), alors il n'appartient pas à lui-même, puisque c'est la propriété des alphas de ne pas appartenir à eux-mêmes. Mais si A n'appartient pas à lui-même, alors il possède exactement la propriété des alphas, donc il appartient à lui-même, puisque par définition ses éléments sont justement les alphas. On a donc un paradoxe dont le schéma est le même que celui du Paradoxe du menteur, à savoir cette équivalence logique :

On aboutit au même schéma de paradoxe quand on affirme l'existence d'un ensemble Oméga ayant TOUS les ensembles comme éléments. C'est le Paradoxe de l'Ensemble plein ou Ensemble de tous les ensembles. C'est le même type de paradoxe quand on parle de l'Ensemble de tous les ordinaux (Paradoxe de Burali-Forti). Car une propriété d'un ordinal est justement de ne pas appartenir à lui-même. C'est en fait les ordinaux qui se cachent derrière les ensembles alphas qui causent le Paradoxe de Russell. Autrement dit, c'est le problème de ce paradoxe qu'on retrouve sous une autre forme sous le Paradoxe de Burali-Forti, et aussi sous le paradoxe de l'Ensemble de tous les cardinaux (Paradoxe de Cantor). Bref, on a affaire au seul et même grand ensemble Oméga (ou Ensemble plein) dans tous ces paradoxes, suivant l'angle sous lequel on voit cet ensemble : Dernier ensemble, Dernier ordinal, Dernier cardinal, etc.

C'est le problème de clôture des ensembles qui se pose ainsi, qui est aussi le problème de clôture des mathématiques et plus généralement des sciences ! C'est cette impossibilité (apparente) de clôture des ensembles que Gödel démontre dans ses célèbres théorème d'incomplétude. On a dit beaucoup de choses sur l'implication philosophique de ces théorèmes, mais en ignorant leur vrai sens : le paradigme actuel est trop faible, trop pauvre, trop restreint, pour pouvoir contenir toute la logique, toute la mathématique et encore moins toute la science ! Avec ce paradigme, des questions ne peuvent que rester à jamais en déhors des sciences, et à plus forte raison des mathématiques ! C'est dont le vrai sens des théorème d'incomplétude de Gödel !

Pour rendre enfin complètes les mathématiques, ou simplement pour résoudre vraiment les le problèmes des paradoxes, on doit changer de paradigme. Sinon, la solution que l'on pense avoir apportée au problème n'est qu'une fausse solution. On n'a fait que réculer le problème, et même pire, on est tombé de Charyde en Scylla !

Le Théorème de l'Existence

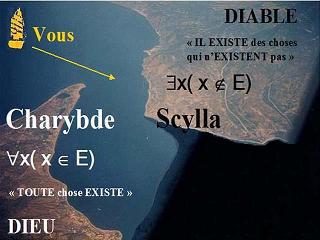
Théorème de Dieu contre Axiome du Diable

Bâtissons une nouvelle science avec comme mot-clef le mot général "CHOSE". Une CHOSE est TOUT ce dont on parle, indépendamment de l'EXISTENCE de la chose en question ! Si c'est une chose qui EXISTE, alors on l'appelle une EXISTENCE. Sinon elle reste simplement une CHOSE dont on parle. Ainsi donc, Dieu par exemple est une chose ! On peut lui refuser peut-être le droit d'EXISTER, mais on ne peut pas lui refuser le droit d'être une CHOSE dont on peut parler !

La seconde notion qu'on se donne pour la science nouvelle est celle d'EXISTENCE, le verbe EXISTER, dans son sens le plus intuitif. Ce qui EXISTE est ce qui est EFFECTIF, REEL ! Ce qui est une REALITE, une VERITE, une POSSIBILITE, etc.

On se donne comme troisième mot scientifique, la notion d'ENSEMBLE, dont le sens naturel est de parler de l'ENSEMBLE de tout ce qu'on veut, des nombres, des arbres, des étoiles, des humains, etc.

Plaçons-nous maintenant dans l'ENSEMBLE de TOUTES les choses, qui par définition sera appelé l'Univers ou Oméga. Il s'agit ici d'une DEFINITION mathématique de l'Univers, et non pas de conception subjective, plus ou moins philosophique. Quand on définit bien les choses, on sait maintenant exactement de QUOI on parle !

L'ENSEMBLE des choses qui EXISTENT est une partie de l'Univers ainsi défini (l'ENSEMBLE de TOUTES les choses). Il en est un sous-ensemble, qu'on appellera Existence ou E. Dieu est un élément de l'Univers, mais pas forcément de l'Existence, puisque son EXISTENCE reste à démontrer, plus scientifiquement en tout cas, ce que je suis en train de faire justement.

Et maintenant, considérons la phrase suivante : "TOUTE chose existe". Tout BON logicien reconnaîtra immédiatement le quantificateur universel (le mot "TOUT") relativisé ici au mot "CHOSE". Appelons cette phrase "Charybde". Si elle est démontrée, elle implique immédiatement que la chose nommée Dieu existe, peu importe ce qu'on entend par ce mot !

Si on veut éviter Charybde (si on veut donc NIER cette phrase), alors qu'on demande l'aide du logicien. Il sait que le contraire de cette phrase est exactement celle-ci : "IL EXISTE des choses qui n'existent pas". Aavec ici le quantificateur existentiel (l'expression "IL EXISTE") relativisé toujours au mot "CHOSE".

Toute personne ayant un minimum de bon sens, à plus forte raison le logicien, voit qu'il y a un problème dans cette phrase "IL EXISTE des choses qui n'existent pas". Il y a une contradiction ! En effet, avec le quantificateur existentiel on affirme l'EXISTENCE des choses, pour les NIER juste après ! Appelons cette phrase "Scylla".

Et la question de l'existence de Dieu est un simple choix entre Charybde et Scylla ! Celui qui NIE l'existence de la moindre chose (et en particulier de la chose nommée Dieu), NIE donc Charybde qui dit que "TOUTE chose existe". Il tient donc pour vérité Scylla qui dit : "IL EXISTE des choses qui n'existent pas".

Mais, seulement voilà : cette phrase est contradictoire. Voilà démontré méthodiquement et scientifiquement que non seulement celui qui NIE la moindre existence ou la moindre possibilité a infiniment plus de chances de se tromper que celui qui affirme TOUTES les existences, mais il se trompe tout simplement !

Logique continue et Logique alternative !

Négation absolue et Négation relative

Le Théorème de l'Existence est la simple démonstration que la notion de NON existence est paradoxale. A moins de fonctionner désormais avec une nouvelle logique qui dit qu'une chose qui n'existe pas existe toujours autrement, que le contraire de toute vérité est toujours une AUTRE vérité, etc. Alors la notion de négation (le connecteur NON) est une négation relative et non plus absolue comme présentement. Toute négation est toujours relative à un contexte donné. Ce qui n'est pas vrai dans un contexte est toujours vrai dans un autre contexte. Ce qui n'existe pas ici ou dans ce contexte existe toujours dans un autre contexte. Ce qui n'est pas possible ici ou dans ce contexte est toujours possible dans un autre contexte, etc.

La négation relative implique une toute nouvelle conception du VRAI et du FAUX, puisque le contraire de toute vérité est toujours une AUTRE vérité. La négation relative est ce que j'appelle l'alternation, du mot ALTER ou AUTRE. La nouvelle logique est ce que j'appelle la Logique d'Alter ou Logique de Cycle (ou Logique cyclique), par opposition à l'actuelle logique scientifique et paradigme, que j'appelle Logique de Non ou Logique de Droite.

L'Equivalence avec NON

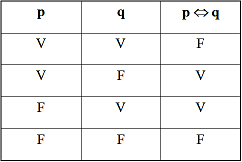
La conception de la négation détermine toute la logique ! Avec l'actuel connecteur NON (la négation absolue), voici la table de vérité de l'équivalence logique (<=>).

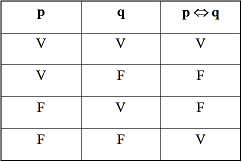
Il en résulte (lignes 1 et 4) que les deux équivalences permises par la négation actuelle sont :

VRAI <=> VRAI et FAUX <=> FAUX.

Dans l'arithmétique et l'algèbre fondées sur cette négation, seules les égalités de type suivant sont autorisées :

0 = 0, 1 = 1, bref X = X.

Cette négation interdit donc l'équivalence suivante (lignes 2 et 3) :

VRAI <=> FAUX.

Cette équivalence est appelé un paradoxe. C'est le schéma du Paradoxe du menteur et des paradoxes comme celui de Russell. Dans l'arithmétique et l'algèbre fondées sur cette négation, l'égalité suivane est interdite t:

0 = 1,
et plus généralement l'égalité X = Y entre deux choses différentes X et Y.

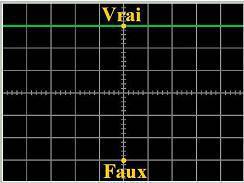
Je qualifie aussi l'actuelle logique de Logique statique ou de Logique continue (par analogie au Courant continu). La raison est que justement ses valeurs de vérités VRAI et FAUX ne varient pas dans le temps, dans l'espace, selon le contexte, etc. Ces valeurs n'alternent pas, le VRAI ne devient jamais le FAUX et vice-versa. On peut donc représenter cette logique par ce diagramme de Courant continu :

 

L'Equivalence avec ALTER

Par contre, je qualifie la nouvelle logique fondée par la négation relative (l'alternation) de logique dynamique ou Logique alternative (par analogie au Courant alternatif). La raison est que justement ses valeurs de vérités VRAI et FAUX varient dans le temps, dans l'espace, selon le contexte, etc. Ces valeurs alternent, le VRAI devient le FAUX et vice-versa. On peut donc représenter cette logique par ce diagramme de Courant alternatif :

 

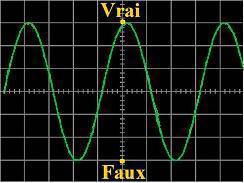
Les deux valeurs de vérité VRAI et FAUX alternent exactement comme les phrases "Il pleut" et "Il ne pleut pas", qui alternent dans le temps et dans l'espace. Cela qui fait que ces deux phrases, bien que contraires l'une de l'autre, sont toutes les deux vraies ! Selon cette logique, une chose qui n'existe pas dans un certain contexte, existe toujours dans un AUTRE contexte, et vice-versa.

Si je demande si la phrase "Théophile est le mari d'Angélique" est vraie ou fausse, la logique actuelle ne peut pas répondre tant qu'on ne lui fournit pas un exemple de Théophile et un exemple d'Angélique. Cette phrase est comme : "X est le mari de Y". Les noms qui y interviennent sont des variables, et c'est pour cela que la logique actuelle ne peut en général fournir de réponse. Il faut pour cela donner des valeurs particulières aux variables, c'est-à-dire on peut répondre que dans le cas de constantes. Les exceptions où on peut répondre à des questions impliquant des variables libres, sont dans le cas d'énoncés du genre ou "p <=> p" ou "X = X", qui sont des tautologies, car satisfaites pour toute valeur de variable. Sinon, en règle générale, pour des énoncés comme "p <=> q", "X = Y", "X est le mari de Y" ou "Théophile est le mari d'Angélique", on ne peut pas répondre par VRAI ou par FAUX. C'est ce qui change avec la négation relative, qui dira simplement que l'énoncé est VRAI et FAUX. En effet, il y a toujours quelque part un Théophile qui est le mari d'une Angélique, et quelque part où un Théophile n'est pas le mari d'une Angélique.

Cela veut dire que la négation relative (ou négation alternative par opposition à négation continue), l'ALTER donc, possède deux tables de vérité. Il y a la table classique qui est :

ALTER Vrai = Faux, et ALTER Faux = Vrai,
exactement comme NON.

Et il y a une autre table, appelée son alternation, obtenue en alternant les résultats selon justement l'équivalence :

VRAI <=> FAUX
qui exprime simplement une permutation des valeurs, une alternance, une alternation !

Cela donne donc :

ALTER Vrai = Vrai, et ALTER Faux = Faux.

De la même façon, en permutant les résultats de la table de l'équivalence, on obtient l'alternation de l'équivalence :

Cette table se résume simplement par : VRAI <=> FAUX, ce qui est la nouveauté même de la nouvelle logique, la logique alternative. Elle ne perd rien de l'actuelle, elle inclut tous ses résultats et sa vérité, auxquelles elles ajoute de nouvelles vérités, qui sont tout ce que l'ancienne nie ou qualifie d'indécidable ! Avec la nouvelle logique tout est décidable, puisque de toute façon tout est vrai ! Ce qui n'est pas vrai est toujours autrement vrai. Le contraire de toute vérité est toujours une autre vérité !

Le retour de Cantor !

Comme dit plus haut, cette nouvelle logique est aussi qualifiée de Logique de Cycle ou Logique cyclique, car justement c'est la logique qui découle du paradigme du Cycle, ainsi que le montrent les deux vidéos Toute la Lumière sur les Paradoxe et l'Algèbre du Cycle, proposées en introduction. Avec cette logique, la négation est donc relative, alternative, cyclique, dynamique, etc., par opposition à la négation absolue, continue, linéiare, statique, etc. A moins de raisonner avec cette autre négation, la notion de NON existence est paradoxale. C'est cette démonstration qui constitue le Théorème de l'Existence qui dit : "Toute chose est une existence" ou "Toute chose existe". Donnons une autre démonstration de ce théorème.

Rappelons que la nouvelle approche de la notion d'ensemble est la Théorie universelle des ensembles, et que sa méthodologie est la théorématique. Contrairement à l'axiomatique, les mots ne sont pas vidés de leur sens intuitif, naturel. Mais bien au contraire, pour résoudre les paradoxes, ce sens est renforcé, et rendu le plus UNIVERSEL qui soit ! Ceci est extrêmement important.

Le premier mot clef de la nouvelle théorie est le mot chose, le mot le plus général, le plus universel, le mot par défaut, en l'absence de tout autre mot. Tout ce dont on parle est une chose, indépendemment de l'existence de la chose en question. Le but du Théorème de l'Existence est justement de régler cette question d'existence une bonne fois pour toutes. Avant donc de parler d'existence, encore faut-il parler des choses au sujet desquelles la question d'existence se pose. Un humain, un animal, un arbre, un caillou, une étoile, l'amour, la vie, Dieu, les anges, le Diable, etc., sont des choses.

Appelons un Adamatwo un "humain qui une taille d'au moins 2 mètres". Le simple fait de dire Adamatwo ou "humain qui une taille d'au moins 2 mètres", c'est parler d'une chose. Et on dira actuellement que ces choses existent, puisqu'on connaît sur terre des humains ayant une taille de plus de 2 mètres. Appelons maintenant un Adamaten un Adamatwo un "humain qui une taille d'au moins 10 mètres". Là encore je parle d'une chose. La question de son existence est une autre affaire, mais ce qui compte pour l'instant c'est qu'il s'agit d'une chose. Dans la nouvelle théorie et approche de la science donc, une chose est TOUT ce dont on parle ! C'est le premier mot clef de cette science.

Le second mot clé est justement la notion d'existence ou le verbe exister. Une chose qui existe est une chose qui est effective, qui a une réalité, ainsi qu'on conçoit simplement et naturellement cette notion d'existence. Par définition, une existence est une chose qui existe, étant entendu qu'elle puisse ne pas exister.

La troisième notion clé est la notion d'ensemble, là encore dans son sens le plus INTUITIF, naturel ! On parlera sans aucun a priori philosophique de l'ensemble des entiers naturels, de l'ensemble des ordinaux, de l'ensemble des cardinaux, de l'ensemble des Adamatwo, de l'ensemble des Adamaten, de l'ensemble des existences,de l'ensemble des choses, de l'ensembles des ensembles, etc. ! Un humain est un ensemble constitué d'éléments ou de parties, un pays est un ensemble, une galaxie est un ensemble, un atome est un ensemble, etc. On ne met donc aucune limite a priori à cette notion. Je vais donc plus loin que Georg Cantor (1845-1918), le père de la théorie des ensembles, qui concevait la notion d'ensemble d'une manière très générale. Il disait : « Par ensemble, on entend un groupement en un tout d’objets bien distincts de notre intuition ou de notre pensée. » L'axiomatique a consisté à restreindre cette conception. Mais la théorématique consiste bien au contraire à la rendre encore plus universelle ! D'où le nom : Théorie universelle des ensembles !

Une autre démonstration du Théorème de l'Existence

Avec les trois mots clés de la théorie bien posés (chose, existence et ensemble), on peut maintenant démontrer le théorème qui fonde la nouvelle science. On commencer par définir trois ensembles :

-> C : Ensemble de toutes les choses, appelé Univers ou Chose
-> E : Ensemble de toutes les existences ou Ensemble de toutes les choses qui existent, appelé Existence
-> N : Ensemble de toutes les NON existences ou Ensemble de toutes les choses qui n'existent pas, appelé Néant.

Pour des problèmes techniques (affichage correct des symboles mathématiques incertain selon les navigateurs), les opérations élémentaires entre les ensembles, intersection et réunion, seront écrits inter et union. La relation d'appartenance sera écrite element, la NON égalité est notée different, et l'ensemble vide sera noté O.

Il est alors évident que : C = E union N, puisque la réunion des choses qui existent (les existences) et des choses qui n'existent pas (les NON existences) constituent l'ensemble de toutes les choses ou C. Et on a aussi : E inter N = O, ce qui signifie qu'aucune chose ne doit être à la fois une existence et une NON existence, selon la conception actuelle de la négation. Si cela se produit, la conception actuelle appelle cela un "paradoxe". Ceci dit, montrons qu'on doit obligatoirement avoir N = O, ce qui signifie que C = E ou Chose = Existence, et alors le théorème est démontré.

Examinons les deux cas N = O et N different O.

-> Si N = O, alors cela signifie que l'ensemble des NON existences est vide, donc "Aucune chose n'est une NON existence", donc "Toute chose est une existence", et le théorème est démontré.

-> Si N different O, alors N est NON vide, ce qui signifie que l'ensemble des NON existences possède au moins un élément, appelé a. On a donc a element N, cet élement a EXISTE donc a est tout simplement une EXISTENCE ! Donc a est à la fois une existence (un élément de E) et une NON existence (un élement de N), ce qui contredit E inter N = O, donc ce qui est un paradoxe. On est donc obligé de conclure que N different O est faux, donc que N = O est vrai, ce qui démontre le théorème. On a donc C = E ou Chose = Existence, ou encore : "Toute chose est une existence". CQFD.

Ainsi est démontré d'une autre manière le Théorème de l'Existence, qui (comme nous l'avons fait dans l'aricle d'introduction "Syn-Thèse pour l'Université) se démontre simplement et directement avec le quantificateur existentiel ("IL EXISTE") et le quantificateur universel ("TOUT"), en faisant juste remarquer que la phrase "IL EXISTE des choses qui n'existent pas" est un paradoxe, donc son contraire : "TOUTE chose existe" est un théorème.

Le théorème dans toute sa généralité

Plus généralement, peu importe le mot M qu'on se donne, la phrase "IL EXISTE des M qui n'existent pas" est un paradoxe, donc son contraire "TOUT M existe" est un théorème ! Par exemple, la phrase "IL EXISTE des cailloux qui n'existent pas" est un paradoxe, donc "Tout caillou existe". De même, la phrase "IL EXISTE des univers qui n'existent pas" est un paradoxe, donc "Tout univers existe". Peu importe donc le mot M (que ce soit chose ou autre) ce n'est pas au niveau du mot que le problème se pose, mais avec la notion d'existence, le fait de NIER une existence, quelle qu'elle soit ! C'est un problème fondamentalement de LOGIQUE, et plus précisément un problème qui se pose avec la négation, comme examinée plus haut ! NIER l'existence cause un paradoxe, sauf si la négation est relative, alternative, cyclique, dynamique. Alors dans ce cas on fonctionne avec une autre logique, infiniment plus nuancée dans sa négation, qui relativise beaucoup la négation. Avec cette logique, tout est VRAI !

Les deux phrases "0 est différent de 1" et "0 = 1", contraires l'une de l'autre, sont maintenant toutes les deux vraies ! Et pour dire les deux, il suffit d'avoir dit la deuxième, qui est donc une vérité plus forte. En effet, il est déjà acquis que 0 est différent de 1, tout comme il est acquis qu'un lapin est différent du soleil, qu'un noir est différent d'un blanc, qu'une femme est différente d'un homme, etc. La différence est de fait, sinon on ne peut pas parler de DEUX choses X et Y ! Celui qui dit donc "0 = 1" a déjà dit que 0 est différent de 1 ! Cette écriture égalise deux choses différentes, elle exprime quelque chose EN PLUS de la différence, ce qui qui fait qu'elle est une vérité plus riche, plus forte !

La Théorie de l'Universalité

Avec la logique actuelle, la notion de vérité ne peut qu'être très étroite, car elle ne tient pas compte des réalités physiques ! Par exemple, à un instant donné, je suis assis. Si je me lève, il y a donc de ce fait un changement dans ma personne, au moins un changement de ma forme. Si un aspect de ma personne a changé, c'est donc que j'ai changé, je suis devenu différent, ce qui veut dire que mathématiquement, l'être que je suis maintenant n'est pas l'être que j'étais il y a un instant. Et pourtant je parle toujours de moi. Je change donc, et je reste pourtant la même personne. Etre à la fois différent et égal est le propre même des êtres physiques, des êtres dynamiques !

Mais la logique actuelle qualifie de paradoxes des choses qui ont simplement un comportement dynamique, qui réclament donc une logique dynamique, physique ! Dans l'Univers, le contraire de toute vérité est toujours une autre vérité. Ainsi les deux phrases "Il neige" et "Il ne neige pas", bien que contraires, sont vraies toutes les deux. La vérité dépend désormais de l'Espace, du Temps, du contexte. Dans un contexte donné ce sera l'une ou l'autre qui sera vraie. Mais la vérité vue à l'échelle de l'Univers, les deux sont toujours vraies, et il n'y a aucune raison d'éliminer l'une des phrases au détriment de l'autre. La Logique alternative est la logique même pour faire la physique, la science dans tout son ensemble ! C'est la logique pour traiter des êtres dynamiques, et en particulier des êtres vivants. C'est la logique pour parler de TOUT, de la vie, de l'existence, de Dieu ! C'est la logique pour faire la Science du Tout, la Théorie de l'Universalité.