La totalité des mathématiques peut être traitées dans une seule théorie : la théorie des ensembles.
Actuellement, la théorie de référence est la théorie axiomatique des ensembles de Zermelo-Fraenkel.
Cette théorie a été élaborée au début du XXème siècle pour résoudre les paradoxes découverts
dans la théorie des ensembles de Georg Cantor (le père de la théorie des ensembles).
Parmi les notions qui posaient problème, il y avait par exemple :
l'Ensemble de tous les ensembles, l'Ensemble de tous les ordinaux, etc.,
et plus généralement ce qu'on appelle les "grands ensembles".
Mais en réalité tous ces problèmes viennent de ce que la théorie des ensembles ne se déroule pas
dans le cadre le plus naturel où elle devrait se dérouler, le plus grands des ensembles : l'Ensemble de toutes les choses.
Autrement dit, l'Univers TOTAL!
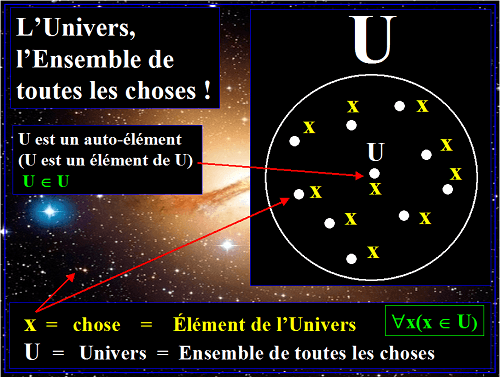
La U_Mathématique est la Théorie universelle des ensembles,
c'est-à-dire la théorie des ensembles qui se déroule dans le plus grand des ensembles : l'Univers TOTAL.
Quand on travaille dans l'Univers TOTAL (l'Ensemble de toutes les choses),
toutes les branches des mathématiques (et aussi des autres sciences) s'unifient en une seule théorie : la Théorie universelle des ensembles.
Mais pour pouvoir faire la Mathématique de l'Univers TOTAL sans rencontrer les paradoxes mentionnés,
il ne faut plus raisonner dans la logique classique.
Celle-ci est trop étroite pour gérer les grands ensembles comme l'Univers TOTAL.
Cet Univers a une structure fractale,
donc nécessite une logique fractale (ou logique cyclique).
Cela signifie aussi qu'il faut changer de conception de l'égalité.
L'actuelle conception de l'égalité est l'identité,
et il faut maintenant travailler avec la notion d'équivalence,
beaucoup plus générale et plus puissante.
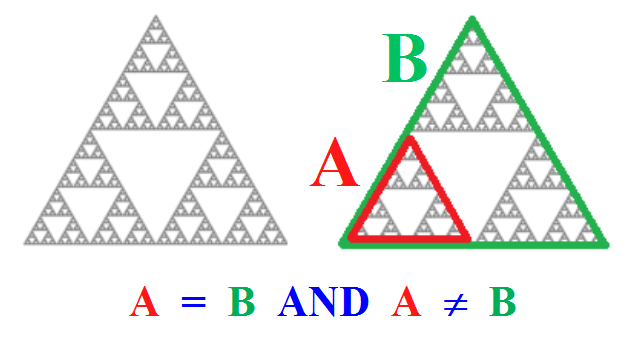
Illustration de la logique fractale avec la Fractale (ou Triangle) de Sierpinski.
Dans la logique classique, affirmer en même temps que "A EST B" et "A N'EST PAS B"
c'est énoncer une contradiction ou un paradoxe, comme les paradoxes trouvés dans la théorie des ensembles de Cantor.
Mais le problème vient de ce qu'on raisonne dans le paradigme de l'identité
au lieu du paradigme de l'équivalence.
Dans l'exemple de la fractale de Sierpinski ci-dessus, A et B ne sont pas la même chose au sens de l'identité, puisqu'il s'agit de deux objets différents.
Et pourtant, A et B sont la même chose au sens de l'équivalence, ils sont équivalents.
En effet, les deux sont le même triangle de Sierpinski à deux échelles différentes.
Toutes les propriétés de A sont aussi celles de B et vice-versa. La seule différence entre eux est que A est une sous-fractale de B.
Ainsi donc, dans le paradigme de l'équivalence, deux choses différentes peuvent pourtant être la même chose!
La notion d'équivalence est très étroitement associée à la structure fractale, mais aussi à la très importante notion de cycle.
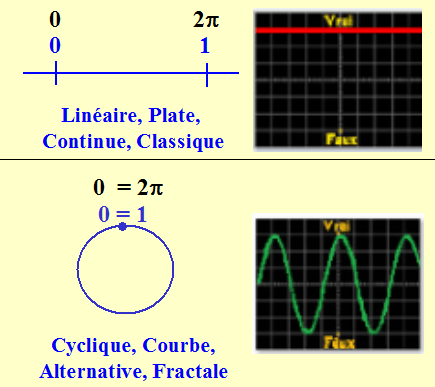
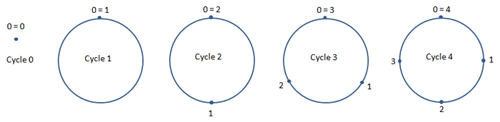
Les égalités du genre "0 = 1", "0 = 2", "0 = 3", "0 = 4" ou encore "0 = 2π",
qui sont des égalités typiques du cycle ou du cercle, sont fausses au sens de l'identité (le paradigme classique).
Mais ces égalités sont éminemment vraies quand on raisonne en logique cyclique.
Ce sont toutes des équivalences, et chaque équivalence correspond à un cycle précis.
Par exemple, "0 = 4" est appelé le "Cycle 4"
(pour plus de détails, voir Nombres Cycliques, Algèbre Fractale, Algèbre Universelle).