Sommaire de cette page :
- L'Univers TOTAL: le VRAI paradigme des nombres. Théorie numérique des ensembles
- - La structure cyclofractale ou omégacyclique des nombres et la division par 0
- - L'Univers TOTAL et les nombres omégaréels
- - Equivalence, Cycle, Fractale, Ensemble Physique, Générescence:
les secrets de l'Univers TOTAL, la vraie nature des NOMBRES!
- - La Générescence de l'Univers TOTAL, les Ordinaux et les Cardinaux.
Le Système de Numération Unaire, la Théorie générescente des nombres
- - La Structure Fractale, l'Equivalence, le Cycle, les Horizons (les très grands nombres), le Dernier Ordinal et l'Infini
- L'Algèbre de l'Univers TOTAL: l'Algèbre de la Générescence, de la FRACTALE, de l'Equivalence, du Cycle
- Voir aussi
L'Univers TOTAL: le VRAI paradigme des nombres. Théorie numérique des ensembles
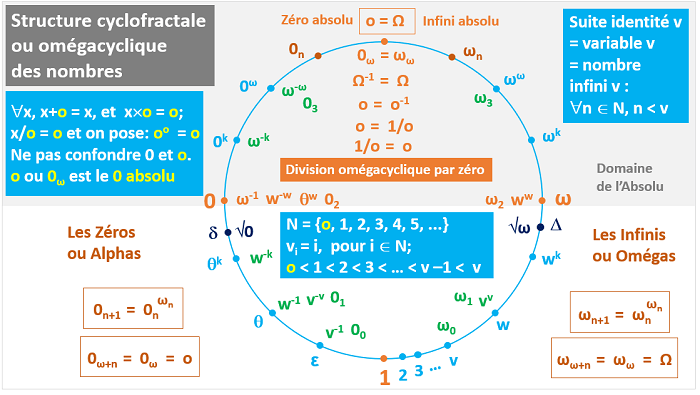
La structure cyclofractale ou omégacyclique des nombres et la division par 0
Equivalence, Cycle, Fractale, Ensemble Physique, Générescence:
les secrets de l'Univers TOTAL, la vraie nature des NOMBRES!

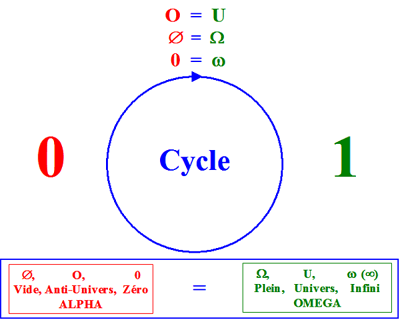
Cliquez sur l'image ou
ici pour regarder la vidéo: L'Algèbre du Cycle,
qui explique la nouvelle définition des nombres dans le paradigme du Cycle et
de l'Equivalence,
mais aussi comment désormais on calcule et on résout les équations dans ce paradigme.
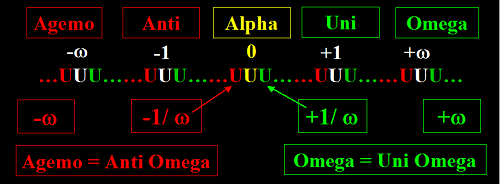
L'Univers TOTAL et les nombres omégaréels
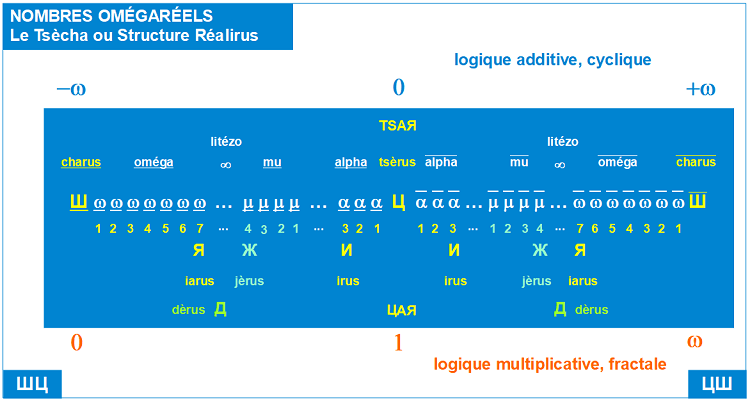
Non, non, ne vous méprenez pas sur ce que veut dire cette image.
Il ne s'agit pas d'une "numérologie russe" mais simplement que le nouveau paradigme scientifique est si riche et si vaste,
que les ressources des alphabets classiques (latin, grec) ne suffisent plus pour exprimer les nouveaux concepts scientifiques.
Alors l'alphabet russe ou cyrillique est appelé à la rescousse, histoire aussi de nous appeler à faire preuve d'ouverture d'esprit...
Pour plus de détails sur l'extraordinaire nouvelle science des nombres qui se cache dans cette image,
voir le livre gratuit de 370 pages:L'Univers TOTAL et les nombres omégaréels

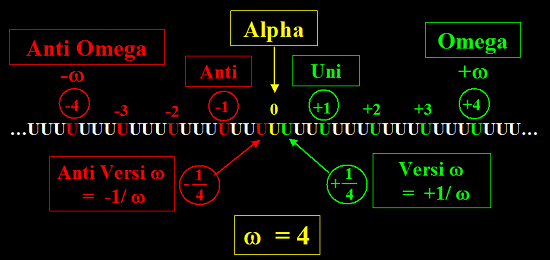
Comme on le lira plus en détail dans le livre L'Univers TOTAL et les nombres omégaréels,
voici comment concevoir les ordinaux (les nombres entiers), du premier d'entre eux, le 0, au dernier
l'infini absolu ω,
pour que la division par 0 soit aussi simple et banale que cette logique de l'horizon.
Que sont ces choses que nous appelons les NOMBRES?
On voit généralement les nombres comme des choses abstraites, des choses purement mentales, ou encore comme des objets du langage pour
dire: "un humain", "deux enfants", "trois lapins", "cinq secondes",
"six mètres", "sept kilogrammes", "huit dizaines", "huit centaines", etc.
Mais ces exemples qu'on vient de donner suffisent largement pour comprendre que les NOMBRES,
c'est bien plus que ce que l'on croit habituellement que c'est.
Par exemple, voici une simple chose à laquelle on n'a sans doute jamais pensé:
tous ces exemples mentionnés obéissent exactement au même modèle:
"N x u", à savoir la multiplication de ce qu'on appelle habituellement un nombre
par une unité,
qui est humain, lapin, mètre, kilogramme,
dizaine, centaine. Et on notera avec grand intérêt que
ces deux dernières unités sont tout simplement des nombres, à savoir 10 et 100.
Tous ces cas nous montrent donc qu'on multiplie un nombre par un humain ou un lapin,
exactement comme on le multiplie par 10 ou par 100, sans aucune distinction!
Il reste maintenant à comprendre simplement que si l'on peut multiplifier un nombre par un humain
comme on multiplie ce nombre par un autre nombre, ou si l'on peut dire: 1 humain + 1 humain = 2 humains,
exactement comme on dirait en algèbre: 1 X + 1 X = 2 X,
c'est tout simplement parce qu'un humain.. est un NOMBRE!
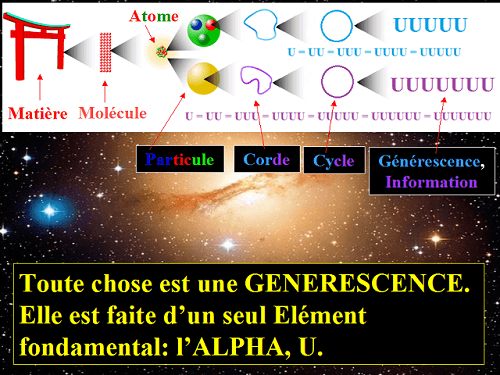
Nous voulons tout simplement faire comprendre aujourd'hui cette vérité que le paradigme de l'Univers
apporte:
"Toute chose est un nombre"!
Et la version informatique de la même vérité est celle-ci:
"Toute chose est une information"!
Quand un nombre est petit ou quand l'information qu'il constitue est simple,
nous l'appelons: trois, douze, cent, mille, etc.,
et en général dans les langues nous ne disons pas: un trois, un douze, un cent,
un mille, etc. (et pourtant on pourrait le dire).
Et quand le nombre est plus grand, nous disons: un million, un milliard,
comme nous disons donc un arbre, une montagne.
Quand le nombre est plus grand ou quand l'information est plus complexe, nous disons:
un mètre, une seconde, un kilogramme, un joule, etc.
et là nous entrons dans le domaine des unités ou des nombres de la physique.
Et quand le nombre est très grand ou l'information très complexe,
on dit un lapin, un humain, une planète, une galaxie, un univers, etc.
Ce qu'il faut comprendre aujourd'hui, c'est que dans tous les cas, nous parlons des NOMBRES!
Le numéro hors série du magazine Science & Vie Junior mentionné plus haut avait raison de titrer:
"Les NOMBRES, ils possèdent les secrets de l'Univers".
Il en est ainsi tout simplement parce que tout dans l'Univers, y compris l'Univers lui-même,
est un NOMBRE!
La notion d'ensemble dont il est maintenant question avec l'Univers TOTAL est celle
d'ensemble physique
(voir La Théorie universelle des ensembles, Théorie physique des ensembles, nouvelle Science de la Matière,
Générescence et Structure FRACTALE).
C'est le paradigme de la générescence et de la structure fractale,
de l'Equivalence,
du Cycle. C'est la vraie nature des nombres.
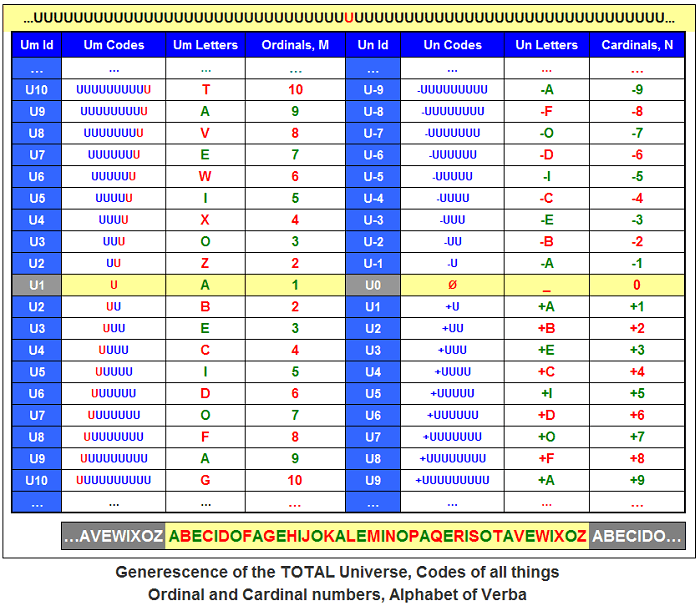
La Générescence de l'Univers TOTAL, les Ordinaux et les Cardinaux.
Le Système de Numération Unaire, la Théorie générescente des nombres
La notion d'ordinal et de cardinal dans le paradigme de l'Univers TOTAL

La structure fractale est le paradigme d'une nouvelle algèbre,
l'algèbre de l'Equivalence,
de la Générescence ou de la Structure Fractale,
dans laquelle on peut dire: U = UUU, c'est-à-dire U = 3U, donc 0 = U,
sans que cela signifie que U est 0 au sens de
l'ontologie de l'Identité.
C'est tout simplement aussi l'Algèbre du Cycle, dans laquelle on peut dire 0 = 1,
là encore sans que 1 soit obligé d'être nul au sens de
l'Identité.
L'Univers TOTAL, U,
l'Ensemble de toutes les choses,
a structure générescente et fractale,
La structure générescente la plus fondamentale de l'Univers TOTAL peut s'écrire:
...UUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUU...
--> D'un point de vue de la physique (voir Théorie physique des ensembles, nouvelle Science de la Matière et Physique Quantique de l'Univers TOTAL, la Physique du TOUT),
cela veut dire tout simplement que toutes les choses de l'Univers TOTAL U
sont physiquement constituées d'un seul constituant élémentaire qui n'est autre que l'Univers TOTAL lui-même, U!
--> D'un point de vue informatique,
cela veut dire que toutes les choses sont des informations unaires,
c'est-à-dire des informations constituées par
une seule information élémentaire, U, ou appelé l'Unit
(par comparaison à Bit pour l'information binaire).
Une information unaire est appelée une générescence
(pour plus de détails, voir Générescence et Structure FRACTALE et Générescence et codage de toutes choses et Le Verba, le Langage Informatique de l'Univers TOTAL)
Les générescences
sont donc: U, UU, UUU, UUUU, UUUUU,....
Ainsi donc, U est la plus petite information qu'on puisse définir,
qui est aussi en même temps la plus grande information, à savoir l'Univers TOTAL!
--> Et d'un point de vue mathématique, cela veut dire que toutes les choses sont des nombres qui s'écrivent dans un système de numération unaire,
d'un seul chiffre: U, qu'on peut aussi noter 0 et appelé Zéro ou Alpha,
mais avec la grande nouveauté que ce nombre initial désigne l'Univers TOTAL, appelé aussi Infini ou Oméga!
Alors les nombres sont donc: U, UU, UUU, UUUU, UUUUU,... ou 0, 00, 000, 0000, 00000, ....
De là on déduit les deux conceptions fondamentales de nombre: les
ordinaux et les cardinaux.

Une générescence
possède deux aspects fondamentaux très liés,
qui sont deux manières différentes de dire simplement la même chose,
à savoir l'aspect ORDINAL et l'aspect CARDINAL.
Avec l'aspect ordinal, on s'intéresse essentiellement à l'ORDRE
des Units dans la générescence,
leur position, leur rang.
De ce point de vue, on parle seulement de Premier (ou numéro Un) ou Alpha,
de Deuxième (ou numéro Deux), de Troisième (ou numéro Trois), etc.,
et de Dernier (ou numéro Infini) ou Oméga.
On notera que du point de vue strictement ordinal (donc où l'on parle seulement d'ORDRE
et non pas de QUANTITÉ, le Dernier d'une séquence
(c'est-à-dire d'un ensemble quelconque de choses disposées en ordre ou considérées dans un ordre),
est appelé l'Infini, et ce peu importe la quantité (ou le nombre au sens cardinal du terme)
de choses concernées dans la séquence: zéro (au sens cardinal du terme), une, deux,
trois, etc., infini (là aussi au sens cardinal du terme).
Donc d'un point de vue seulement ordinal, 4 par exemple ou n'importe quel nombre entier naturel
est un nombre infini, et ceci est fondamental dans la notion de Cycle,
un autre aspect crucial de la générescence.
Et d'un point de vue ordinal, on ignore les nombres 0.5 (ou 0.5 ème)
1/3 (ou 1/3 ème), -2.7 (ou -2.7 ème), etc.
car on ne parle que choses entières, on ne connaît que les nombres entiers, parce que l'ordre
est de nature qualitative et non pas quantitative!
Quand on dit par exemple "deux humains" (ou "premier et deuxième humain"),
on ne se préoccupe pas de savoir si l'un des humains est un adulte de 100 kilos et que l'autre est un enfants de 5 kilos,
mais on les compte tous les deux comme unité à part entière, et pour cela il suffit qu'ils possèdent
la qualité réquise pour être ainsi comptés.
Ici, les choses dont on s'intéresse fondamentalement à l'ORDRE dans un premier temps
puis à la QUANTITÉ dans un second temps,
sont simplement les Units d'une générescence,
les unités U!
La notion cardinal (donc de nombre en tant que quantité)
intervient donc quand on COMPTE les Units,
quand on exprime la QUANTITÉ d'information qu'est une
générescence donnée.
Par exemple, la quantité d'information de la générescence UUUU est 4,
car elle compte fondamentalement quatre Units.
C'est ici qu'intervient une autre notion importante:
à savoir si l'on commence le comptage des Units avec le Premier (ou Alpha),
ou si l'on commence avec le Deuxième!
Dans le premier cas, on compte en disant simplement: 1, 2, 3, 4, 5, ...,
et alors le Zéro est l'Avant-Premier du point de vue ordinal,
et il a le sens de Vide, de Rien, de Néant, etc.
Nous convenons alors de dire qu'on fait un comptage ordinal, car,
intuitivement et naturellement, nous exprimons l'ordre en disant
Premier (ou numéro Un),
Deuxième (ou numéro Deux), etc.
et en général pas en disant Zéroième (ou numéro Zéro),
bien que rien n'interdise de la dire.
Mais l'usage naturel est de commencer par le Premier (ou numéro Un)...
Mais dans le second cas, on compte en disant simplement: 0, 1, 2, 3, 4, ...,
et alors le Zéro est le Premier du point de vue ordinal,
et il a le sens d'Origine, de Référence, etc.
Nous convenons alors de dire qu'on fait un comptage cardinal,
car, là aussi naturellement et intuitivement,
nous exprimons les quantités en ayant conscience du cas particulier
où il n'y a rien à compter, et où nous disons "Vide", "Rien" ou "Néant".
Mais seulement, historiquement, l'humain a eu des difficultés psychologiques
à concevoir que ce "Vide" doit être aussi un nombre
à par entière qui doit intervenir dans la numération et dans les calculs.
Le cardinal Zéro était conçu intuitivement, mais traduit en écriture numérique
que laborieusement.
Le Zéro ordinal (Ø ou O) et l'Infini ordinal (Ω ou W). Le Zéro cardinal (0) et l'Infini cardinal (ω)
La notion cardinale d'Infini est très simple aussi
quand on s'appuie sur la générescence.
L'Infini, actuellement appelé Infini dénombrable
mais que nous appelons aussi Infini défini (ou même Infini-fini!)
et qui est habituemment noté ω (ou Oméga),
est le tout simplement le nombre des éléments de l'ensemble N des entiers naturels:
0, 1, 2, 3, 4, 5, 6, ....
C'est tout simplement aussi le nombre d'Units de la
générescence infinie
notée: UUUUUUU..., le symbole "...", que nous appelons le
GENER
indique simplement la séquence des Units se poursuit indéfiniment, qu'elle est aussi grande et aussi longue que l'on veut,
mais tout en restant toujours FINIE! Autrement dit, le nombres des Units
de cette générescence est toujours un certain entier naturel!
On ne s'en rendait pas compe, mais la Logique classique
(et plus généralement la Logique Négative)
avec laquelle on a raisonné et fait les mathématiques et les sciences jusqu'ici
faisait que ces sciences, quand bien même elles sont réputées exactes comme les mathématiques,
cachaient dans leurs fondements de profonds paradoxes,
que l'on a cru à tort avoir résolu lors de la crise des fondements des mathématiques survenue
au début du XXème siècle.
La Logique Négative (entre autres la Logique classique),
la logique du "Tout ou Rien" est resposable de nombreux paradoxes,
tout simplement parce que cette logique à elle seule ne suffit pas
pour nous faire accéder à toute la vérité scientifique,
à toutes la diversité et la subtilité des choses dans l'Univers.
Parmi les nombreux paradoxes dont le paradigme de la Négation
(ou, ce qui revient au même, de l'Identité)
est responsable, il y a le Paradoxe Sorite,
qu'on peut appeler le paradoxe de la logique du Tout ou Rien.
Autrement dit, cette logique devient paradoxale quand elle est appliquée à des situations
où il ne faut pas raisonner en termes de Tout ou Rien mais dans une logique supérieure ou plus fine,
une autre logique que cette logique grossière habituelle, qui n'est pas faite pour ces cas-là.
Exemples simples: Avoir un seul poil au menton, ce n'est pas être barbu.
Mais en avoir des millions et des millions, c'est être barbu.
Alors à partir de quel nombre de poils exactement on cesse d'être imberbe pour devenir barbu?
De même, avoir un seul cheveu sur le crâne ce n'est pas encore être chevelu mais c'est être chauve.
Avec des millions et des millions de cheveux on est chevelu.
Et alors à partir de quel nombre exactement de cheveux on passe de l'état de chauve à l'état contraire de chevelu?
Si l'on raisonne en terme de Tout ou Rien (comme on le fait habituellement),
en terme de chauve ou de non-chauve, etc.
(comme on le fait dans la Logique Négative ou la logique binaire),
on est ici dans un cas typique de Paradoxe Sorite.
Ce Paradoxe se ramène tout simplement aux problèmes suivants, qui implique les nombres ou les ordinaux:
Si l'on convient par exemple que 1 est un nombre entier naturel petit
et qu'en revanche 1010 000 000 000 ou
"10 puissance dix milliards" (nombre que nous appelons Lhorizon 3)
est un entier naturel grand (à plus fortes raisons les nombres infiniment plus monstrueux et au-delà de tout entendement
comme Lhorizon 7, Lhorizon 1000, Lhorizon 1000000000, ..., etc.),
alors la simple question est de savoir à partir de quel nombre exactement on cesse d'être dans
le domaine des petits nombres et que l'on rentre dans le domaine des grands nombres.
Et c'est exactement la même question qui se pose quand il s'agit de savoir
à partir de quand exactement un nombre cesse d'être fini pour devenir infini.
La Logique Négative
conduit à une théorie des ordinaux et des cardinaux dans laquelle les nombres entiers naturels
sont tous appelés des nombres "finis", donc aussi des nombres monstrueux comme
par exemple Lhorizon 3 ou
Lhorizon 10000000000000000000,
ce qui est une aberration!
Tout le problème est dans cette écriture qui illustre la logique de la classique théorie des ordinaux:
{0, 1, 2, 3, 4, 5, 6, 7, ..., ω, ω+1, ω+2, ω+3, ...}
Comme on le voit, avec des pattes de "super-kangourous", on "saute" étrangement du domaine du fini (auquel appartient l'ordinal 7 par exemple),
pour commencer à entrer dans le domaine des ordinaux et des cardinaux infinis,
le premier d'entre eux étant Aleph zéro, habituellement appelé Oméga
et noté ω. Pour arriver donc à ω,
on "saute" la zone des "trois points", zone indiquée par le symbole habituel "..." que nous
appelons le GENER.
Sauter le GENER
est facile à dire qu'à faire!
On le fait aisément quand on nage dans la pure abstraction et quand on ne se rend pas bien compte de ce que l'on fait
et des paradoxes qui peuvent se cacher dans la pratique des mathématiques et des sciences.
On dit alors par exemple que ce premier ordinal (et cardinal) ω,
qui ouvre la porte du royaume de l'infini, n'a pas de prédécesseur, car son
prédécesseur, ω-1 donc, serait dans le domaine des finis,
ce qui par voie de conséquent entraîne que ω est lui-même fini,
car ajouter 1 à un nombre fini, c'est avoir un nouveau nombre fini.
C'est tout simplement un Paradoxe Sorite
(ici le Paradoxe Fini-Infini) dû simplement au fait que l'on raisonne en Logique Négative,
la logique du Tout ou Rien, qui est ici inappropriée pour la question du Fini-Infini
(voir aussi Le Problème de l'Infini).
Toutes les questions de l'Univers ne se traitent pas en terme de Tout ou Rien,
de Vrai ou Faux, de Blanc ou Noir, de Oui ou Non.
Cette logique est faite uniquement pour trancher quand il faut trancher et
savoir si oui ou non on va faire un troisième enfant, si l'on ira ou non demain à la foire de Lille,
si oui ou non on va acheter le dernier ordinateur,
si oui ou non on va bâtir la science sur le paradigme de l'Univers TOTAL, etc.
Mais les questions scientifiques ou relatives à l'Univers ne se traitent pas toutes en ces termes-là, loin de là!
Beaucoup de questions appellent une logique nuancée,
au moins à trois valeurs de vérité (par exemple, Vrai, Faux et Neutre).
Et beaucoup d'autres réclament tout simplement une logique dont la valeur de vérité Vrai est graduée
de 0 (ou 0%) à 1 (ou 100%).
Par exemple, à la question de savoir si le nombre 2 est le dernier nombre entier naturel
(donc le plus grand, l'infini, etc.), la Logique Négative habituelle
dégainera la réponse "Non!", plus vite que son ombre, à la vitesse de l'éclair,
sans autre forme de procès! Et à la question de savoir si 3 est le dernier nombre entier naturel,
ce sera toujours le même "Non!" catégorique. Pareil pour 10,
pour 1000, pour 10000000000000, pour 1010 000 000 000, etc.
A chaque fois la Logique Négative dira
"No!", ou "Niet!", ou "Nada!", ou "Walou!", ou "Kpèdè!",
et ce sans appel! Cette logique grossière du Tout ou Rien ne tient pas compte du fait évident que
le nombre dont on parle évolue, et donc que la question évolue aussi,
de même que la réponse qu'elle appelle, qui doit être nuancée!
Et maintenant, avec la Logique Alternative,
on découvre que, aussi étonnant que cela puisse paraître, l'idée que
2 est le dernier nombre entier naturel n'est fausse que de 1/2 (ou 50%)
donc vraie à 1/2 (ou 50%)!
Et l'idée que 3 est le dernier nombre entier naturel
n'est fausse que de 1/3 (ou 33%)
donc vraie à 2/3 (ou 67%)!
Avec 10 on passe à 1/10 (ou 10%) pour le faux
et à 9/10 (ou 90%) pour le vrai! Etc.
Et alors, éclairée par cette logique fine, la vérité mathématique change du tout au tout,
et des paradoxes très cachés et très vicieux
ignorés actuellement apparaissent
(voir aussi par exemple Le Paradoxe de la Variable
et d'autres diables de ce genre très cachés au fin fond de la pratique scientifique actuelle).
Par exemple aussi, la question de savoir si oui ou non le nombre π
est un nombre rationnel (une fraction),
malgré la réponse apparemment juste qu'apporte la Logique classique (elle dit que π est irrationnel),
cette réponse est pourtant "fausse" quand on raisonne maintenant en
Logique Alternative.
"Fausse" en ce sens que la valeur de vérité de la phrase "π est irrationnel"
est quasi nulle, elle est infinitésimale, elle tend vers 0 ou 0%,
tandis que bien au contraire, c'est la valeur de vérité de son contraire,
"π est rationnel" qui tend vers 1 ou 100%!
Qui l'eût cru? Comme quoi...
(pour plus de détails, voir le sous-titre Dans le paradigme de Cycle, tout nombre réel est un nombre rationnel
et plus généralement le soust-tire Dans le paradigme du Cycle, tout nombre réel est un nombre entier naturel!).
Ne sous-estimons surtout pas le potentiel des nombres entiers naturels!
N'allons pas chercher d'autres notions d'infinis que celle qu'ils contiennent déjà, et comment!
Des nombres infinis plus féconds, dont les propriétés sont plus riches, plus extraordinaires,
justement parce qu'ils cumulent aussi toutes les qualités des nombres finis!
Un cheval volant qui peut faire tout ce que peut faire un cheval mais qui peut voler aussi comme un oiseau,
est infiniment plus intéressant qu'un cheval qui ne vole pas ou qu'un oiseau qui ne peut pas courir comme un cheval!
Ainsi en est-il des nombres infinis qui sont finis aussi, ou des nombres finis qui sont aussi infinis!
{0, 1, 2, 3, 4, 5, 6, 7, ..., ω, ω+1, ω+2, ω+3, ...}
Il ne faut pas "sauter" le GENER
(les "trois points" ou "...")
comme des sauvages pour aller vers des nombres infinis dont l'arithmétique devient très pauvre pour cette raison-là
(parce qu'il leur manque de très précieuses propriétés de l'arthmétique du fini).
Mais il faut prendre le temps d'examiner la zone du
GENER
et les extraordinaires nombres entiers de transition qu'ils cachent,
ceux qui mettent fin au Paradoxe Sorite,
ceux qui font le pont entre le royaume des finis et celui des infinis.
Il suffit de prendre en considération des nombres phénoménaux comme
Lhorizon 3, Lhorizon 7, Lhorizon 1000, Lhorizon 1000000000, ..., etc.
mais aussi le fait (c'est très important!) que pour un tel nombre entier gigantesque ω donné,
la phrase "ω est le dernier ordinal" ou "ω est le dernier nombre entier"
ou encore "ω est l'infini", n'est fausse que de 1/ω,
et elle est vraie à (ω-1)/ω ou 1 - 1/ω!
Que demande le peuple?
En langage plus classique, la fausseté de la phrase "ω est le dernier ordinal" ou
"ω est l'infini" tend vers "Zéro"
quand le nombre entier naturel ω dont on parle tend justement vers... l'"Infini"!
Evidemment! Si cette simplement vérité (que l'on doit maintenant à la Logique Alternative
et à sa finesse) est maintenant comprise, alors on a compris aussi
qu'il n'existe fondamentalement qu'un seul Infini,
celui qui mesure le cardinal, le nombre ou la quantité des éléments de l'ensemble des entiers naturels.
Toute autre notion d'Infini n'est qu'un aspect de cet Infini fondamental,
une manière plus ou moins déguisée de parler du même être fondamental.
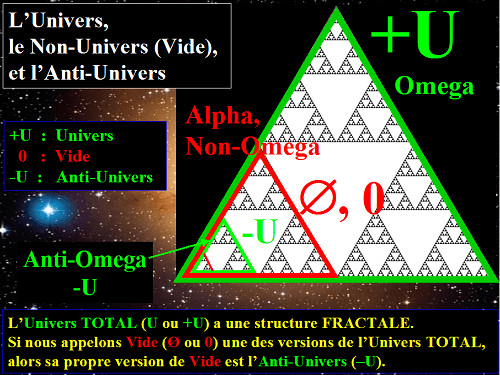
Pour comprendre pourquoi, il suffit de regarder une structure fractale
comme par exemple celle très pédagogique de Sierpinski
(à ce propos voir le sous-titre La Structure Fractale, l'Equivalence, le Cycle, le Dernier Ordinal et l'Infini)
Ce cardinal de l'ensemble des entiers naturels est à la fois Infini et Fini.
Une vérité difficile à appréhender dans le très restreint paradigme actuel de
l'Identité,
mais qui devient chose très simple et très banale dès qu'on travaille très confortablement
dans le nouveau paradigme de l'Equivalence,
du Cycle (ici étudié), de la Générescence et de la Structure Fractale,
bref de l'Univers TOTAL
(voir aussi Le Problème de l'Infini)!
Cette vérité s'exprime par la simple équivalence:
0 = ω, qui est l'expression générale du Cycle.
Elle signifie que le Premier ordinal est aussi le Dernier ordinal,
et que l'un comme l'autre désigne le seul et même Univers TOTAL,
le seul et même Ensemble de toutes les choses!
Cette vérité peut s'écrire aussi:
1 = ω+1, ce qui signifie alors que l'on commence à compter les Units de la générescence
en disant "Un" et non pas "Zéro".
Et alors, de même qu'on parle
d'"Avant-Premier" pour parler du "Zéro ordinal",
il faut maintenant parler exactement de la même façon de la très étrange notion
d'"Après-Dernier", qui n'est pas plus paradoxal que de parler d'"Avant-Premier".
Il suffit maintenant de comprendre que ce sont simplement des notions du paradigme et du langage du Cycle,
et que dans ce langage, il existe toujours un avant-commencement qui est la fin du cycle d'avant,
et qu'il existe aussi toujours un après-fin qui est le début du cycle d'après.
Il n'y a donc plus de mystères ou de difficultés quand on raisonne dans les bons paradigmes.
Et maintenant, de même qu'on a inventé le mot "Zéro" ou "0"
pour parler de ce qui est avant le "Premier" ou le "Un" ou "1",
il faut maintenant aussi inventer un mot pour parler de "ω+1", ce qui est donc
après le "Dernier" ou l'"Oméga" ou "ω".
Je ne me casse pas la tête, je l'appelle l'"Omégun",
ce qui veut dire que c'est un nouveau "Un", mais après l'"Oméga",
donc dans le nouveau cycle qui commence.
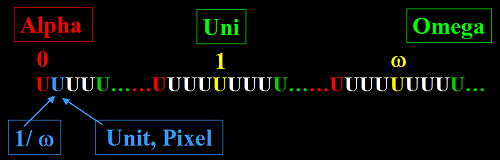
Les deux notions de Zéro, associées respectivement à deux notions d'Infini.
Au sens ordinal, le Zéro et l'Infini signifient simplement
Premier et Dernier,
et ce peu importe le nombre de choses dans la séquence où l'on parle de Premier et de Dernier!
Ce sens ordinal des deux notions est absolu, il est général, simplement qualitatif.
Et au sens cardinal, le Zéro signifie 1/Oméga ou 1/ω.
Il dépend alors du nombre entier ω pris comme Infini,
et plus ce nombre est grand et plus vraies sont les notions respectives d'Infini et de Zéro!
Au sens le plus général du terme, une générescence
est appelée un univers,
car une générescence
est une chose constituée d'une seule chose fondamentale qui est l'Univers TOTAL, U.
Et alors dans ce cas la quantité d'Units de la générescence
est tout simplement Infini cardinal, l'Oméga (ou ω).
Et alors 1/ω (le Zéro cardinal) est appelé aussi
la résolution de l'univers ou de la
générescence
(au sens informatique du terme, et on parle alors aussi de Pixel),
ou la finesse de l'univers ou son paramètre de structure fine
(et là on voit la question plutôt du point de vue de la physique).
Ainsi donc, nous avons deux notions de nombres (ou deux manières de voir la même notion de nombre),
les ordinaux et les cardinaux, deux manières de considérer
les générescences:
d'abord du point de vue qualitatif qui est simplement l'ordre
et la séquence des Units ou unités d'information; et ensuite d'un point de vue
quantitatif qui est donc la mesure de la quantité des Units,
la quantité d'information (qui est aussi la quantité de matière
si l'on voit la question d'une point de vue de la nouvelle physique quantique).
Il en résulte aussi entre autres deux notions du Zéro et de l'Infini.
D'abord le Zéro ordinal appelé l'Avant-Premier ou l'Avant-Numéro-Un, etc.
Il est appelé le Zéro de position dans le numération, comme par exemple
dans "2011" ou dans 0110001110.
Il est de nature essentiellement INFORMATIQUE, il est avant tout une information,
et en cela il est potentiellement aussi 1, A, U, ou tout ce que veut comme symbole.
Par exemple, pour coder l'infomrmation avec deux informations de base,
on peut faire le choix de A et B,
et alors l'information 0110001110 s'écrit ABBAAABBBA.
Et si l'on fait le choix de U et V,
alors la même information s'écrit UVVUUUVVVU.
Et si l'on fait le choix de 1 et 2,
alors la même information est 1221112221.
On ne fait donc fondamentalement aucune différence entre 0, 1,
A ou U, en tant qu'information,
ou quand c'est pour exprimer l'ordre, la position, etc.
Il en exactement de même pour la notion d'Infini ordinal,
qui veut dire simplement Dernier, peu importe si c'est le dernier dans une séquence de deux choses,
de trois, de quatre, etc. Ainsi, en parlant par exemple de la générescence UUUU, l'infini au sens ordinal
du terme est 4.
Pour se fixer les idées, il faut voir le Zéro ordinal non pas comme le nombre
0 mais comme la lettre O, au même titre que les lettres
A ou U. C'est donc juste une unité d'information.
Très souvent le mot Alpha dans notre langage désignera ce Zéro-là.
En tant qu'ensemble ou le Premier Ordinal
dans le Langage universel des ensembles,
il est noté Ø et il est appelé aussi l'Ensemble Vide.
Mais alors dans ce cas il faut comprendre le Premier ensemble
(celui qui sert à construire les autres) et non pas un ensemble vide dans l'absolu,
qui n'a aucun élément (au sens cardinal des mots "vide" ou "aucun").
Il est "vide" en ce sens qu'on ne considère pas ses propres éléments,
mais on commence tout par cet ensemble, bref il est l'Alpha.
De la même façon, il faut voir l'Infini ordinal non pas comme l'infini
de l'analyse, quand on dit par exemple que "la limite de 1/X quand X tend vers 0 est l'infini"
mais là aussi comme une lettre, W ou même encore U.
Très souvent aussi le mot Oméga désignera cet Infini-là.
En tant qu'ensemble ou le Dernier Ordinal
dans le Langage universel des ensembles,
il est noté Ω et il est appelé aussi l'Ensemble Plein.
Mais alors dans ce cas il faut comprendre le Dernier ensemble
(celui qui est constitué par tous les autres), et non pas "plein" en ce sens qu'au-delà de lui
aucun autre élément n'existe.
En effet, quand on regarde une structure fractale
(comme par exemple la Fractale de Sierpinski
présentée plus loin dans l'examen du Paradoxe du Dernier Ordinal),
elle est l'Ensemble Plein ou Oméga. Et au-delà d'elle il existe des éléments
qui sont de nouvelles versions des éléments de l'ensemble.
Et de même, le modèle choisi comme Ensemble Vide ou Alpha possèdent
d'autres versions des mêmes éléments que l'Ensemble Plein,
ce qui veut dire que le Vide et le Plein sont équivalents.
C'est parce qu'on ne travaillait pas dans le paradigme de l'Univers TOTAL (qui est aussi
le paradigme de l'Equivalence)
qu'on s'est heurté à des paradoxes comme le
Paradoxe de Burali-Forti ou Paradoxe du Dernier ordinal
(dont on reparlera plus loin),
qui n'est autre que le problème de l'Ensemble Plein.
Ceci dit, le problème n'est pas tant de distinguer outre mesure
les notions ordinales des notions cardinales, car ces deux aspects de la générescence
ne sont donc que deux manières différentes de parler de la même chose.
Mais le vrai problème est de ne pas travailler dans le paradigme de l'Univers TOTAL.
Dans le nouveau paradigme, la théorie des ordinaux et des cardinaux (et au-delà toute la théorie des nombres)
se simplifie considérablement. De nombreux problèmes épinueux de l'actuelle théorie des ensembles
et de tout l'ensemble des mathématiques
(comme la très vieille question de la division par 0,
le Paradoxe du Dernier ordinal, l'affaire de l'Axiome du choix,
les casse-têtes de l'Hypothèse du continu,
la dite impossibilité de mettre en bijection l'ensemble des nombres réels et l'ensemble des nombres entiers naturels,
les grille-neurones de la théorie des grands cardinaux
ou des cardinaux inaccessibles, la dite impossibilité de trouver des nombres réels
solutions de l'équation X2 + 1 = 0, etc., etc., etc.)
ne se posent plus. Car en fait c'était de faux problèmes, dus aux paradigmes de
la Négation
et de l'Identité dans lesquels on travaille
(voir aussi Le Problème de l'Infini).
Les Ordinaux et les Cardinaux Linéaires
Dans le paradigme de l'Univers TOTAL, le paradigme de l'Equivalence et du Cycle,
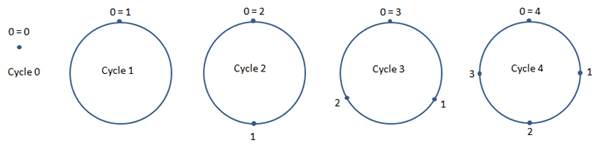
les nombres ordinaux et les nombres cardinaux sont des cycles.
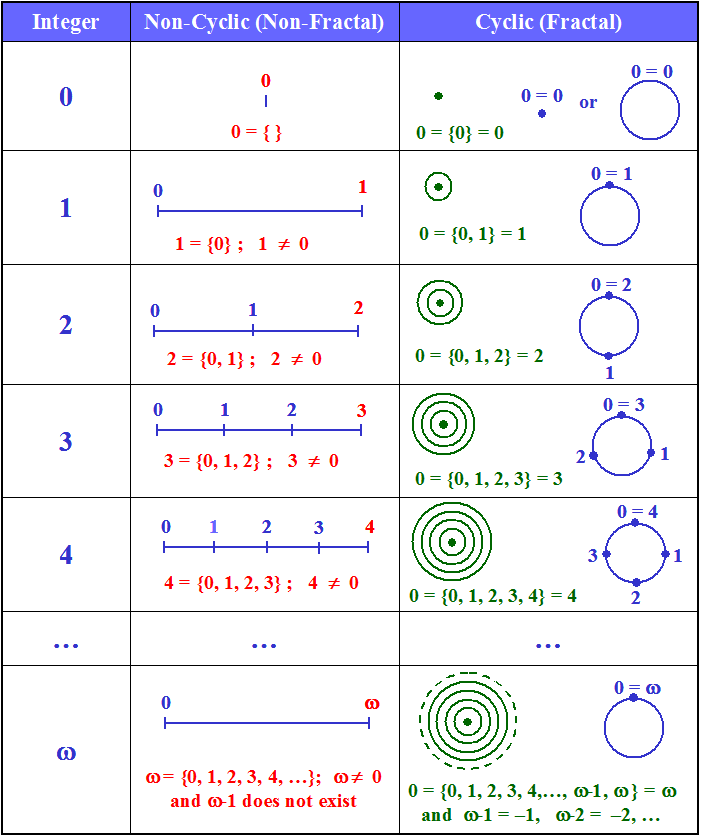
Cela veut dire tout simplement que la bonne représentation des nombres
n'est pas de les placer sur une Droite mais sur un Cercle.
Sauf justement si cette Droite est définie comme un Cercle de rayon infini.
Quand on dispose les ordinaux et les cardinaux sur une Droite,
la situation est alors comme le vieux problème des poteaux et des intervalles.
Les ordinaux sont à interpréter comme le nombre de poteaux (parce que l'on commence alors par "Un" ou "Premier"),
et les cardinaux à interpréter comme le nombre des intervalles correspondants (parce que l'on commence par "Zéro"):
1 poteau: 0 intervalle
2 poteaux: 1 intervalle
3 poteaux: 2 intervalles
4 poteaux: 3 intervalles
Etc.
Définition générescente des ordinaux (ici les numéros d'ordre) et des cardinaux (ici les nombres entiers naturels) :
1: U = 0
2: UU = 1
3: UUU = 2
4: UUUU = 3
5: UUUUU = 4
6: UUUUUU = 5
7: UUUUUUU = 6
...
La définition des ordinaux et des cardinaux est indépendante de la chose choisie pour servir d'Unit:
1: 0 = 0
2: 00 = 1
3: 000 = 2
4: 0000 = 3
5: 00000 = 4
6: 000000 = 5
7: 0000000 = 6
...
1: X = 0
2: XX = 1
3: XXX = 2
4: XXXX = 3
5: XXXXX = 4
6: XXXXXX = 5
7: XXXXXXX = 6
...
1: ω = 0
2: ωω = 1
3: ωωω = 2
4: ωωωω = 3
5: ωωωωω = 4
6: ωωωωωω = 5
7: ωωωωωωω = 6
...
Les Ordinaux et les Cardinaux Cycliques
Le paradigme de l'Univers TOTAL, on l'a dit, est le paradigme de l'Equivalence.
Cela veut dire que la nouvelle conception de l'Egalité
n'est plus la très étroite l'Identité
mais l'Equivalence.
Quand maintenant on écrit une égalité "X = Y",
cela ne veut plus dire que X et Y sont strictement la même chose
(au sens de l'Identité)
mais que X et Y sont la même chose d'un certain point de vue,
à préciser si ce n'est pas évident.
Par exemple, un homme nommé X et une femme nommée Y
ne sont pas strictement la même chose, mais les deux sont équivalents du point de vue de leur appartenance commune à l'ensemble des humains.
De ce point de vue, on a donc "X = Y".
Par exemple aussi, les nombres: -9, -6, -3, 0, 3, 6, 9, ne sont sont pas strictement la même chose,
mais ce sont des multiples de 3. Ils sont équivalents de ce point de vue,
et on écrit donc:
-9 = -6 = -3 = 0 = 3 = 6 = 9
Cette équivalence est que nous appelons le Cycle 3,
et elle est définie par la seule donnée de l'équivalence "0 = 3" ou aussi "1 = 4" ou "2 = 5", etc.
Cette équivalence ou ce cycle, c'est tout simplement la définition du nombre 3
comme nombre cyclique. Ce cycle, en termes de générescence est donc l'équivalence suivante:
U = UUUU ou UU = UUUUU
Ainsi donc le Cycle 1 est l'équivalence:
0 = 1 = 2 = 3 = 4 = 5 = 6 = 7 = ...
c'est-à-dire donc l'équivalence entre tous les nombres entiers naturels, équivalence qui s'écrit en terme de générescence:
U = UU = UUU = UUUU = UUUUU = ...
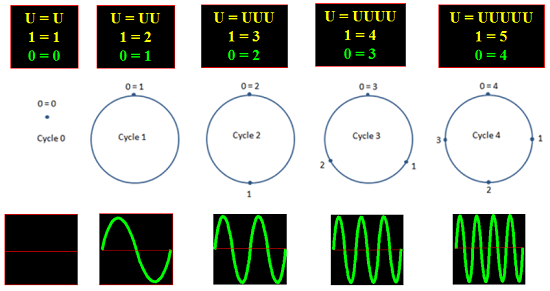
Générescences, Cycles et Ondes (Vibration des "Cordes").
A chaque générescence est associé un ensemble de cycles qui sont autant de types d'ondes.
Chaque cycle est une fréquence donnée,
par exemple le Cycle signifie 3 périodes par unité, ou 3 sous-cycles du Cycle 1.
Le reste est une affaire de propriétés mathématiques des nombres.
C'est ce qui fait la différence entre une chose et une autre dans l'Univers TOTAL.
Au stade le plus fondamental, toute la physique est de la mathématique et de l'informatique pure!
A ce stade, on ne sépare plus ces domaines, car ils sont un seul et même domaine.
Autrement dit, au stade le plus fondamental, toute chose est un nombre, une information!
On ne se demande plus: "Quelle chose existe dans l'Univers et quelle chose n'existe pas",
car on ne se demande pas: "Quel nombre existe et quel nombre n'existe pas"!
(Voir le Théorème de l'Existence)
Quand on dispose les nombres non plus sur une Droite mais sur un Cercle,
le nombre de poteaux est exactement aussi le nombre d'intervalles, ce qui veut dire que les notions d'ordinal
et de cardinal deviennent la même notion.
Autrement dit, avec les nombres cycliques, on ne distingue plus fondamentalement les ordinaux et les cardinaux.
La Structure Fractale, l'Equivalence, le Cycle, les Horizons (les très grands nombres), le Dernier Ordinal et l'Infini
Le Paradoxe de Burali-Forti ou paradoxe du Dernier Ordinal: un faux paradoxe, un problème dû à de mauvais paradigmes et la Négation absolue
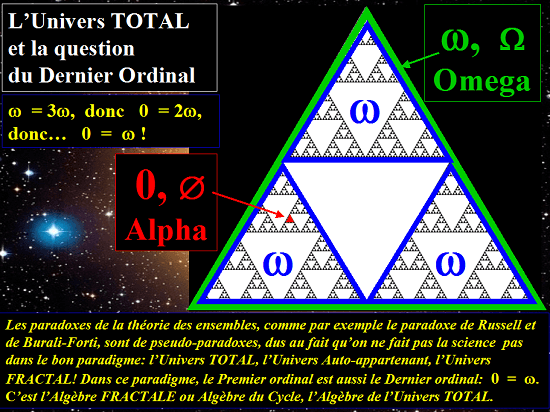
Comment la structure fractale
montre très simplement
l'équivalence entre le premier et le dernier ordinal:
Alpha = Omega ou 0 = ω.
Une équivalence entre l'Infiniment petit et l'Infiniment grand,
entre le Vide et le Plein, entre le Zéro et l'Infini.
Dans les théories axiomatiques des ensembles actuelles (comme par exemple celle de Zermelo-Fraenkel nommée ZF),
on travaille avec l'Ensemble Vide mais sans l'Ensemble Plein!
On travaille avec un Premier Ordinal, qui est justement l'Ensemble Vide, appelé le Zéro,
mais sans Dernier Ordinal, car celui-ci provoque un paradoxe, nommé le Paradoxe de Burali-Forti
Mais en réalité, ces paradoxes et d'autres sont simplement dus au fait qu'on fait la science
dans le très étroit paradigme de l'Identité
au lieu du très large paradigme de l'Equivalence,
ou, ce qui revient au même, on raisonne aved la négation absolue.
Les nombres, et en particulier le Dernier Ordinal réclament tout simplement le paradigme l'Univers TOTAL,
l'Univers FRACTAL, le paradigme de l'Equivalence.
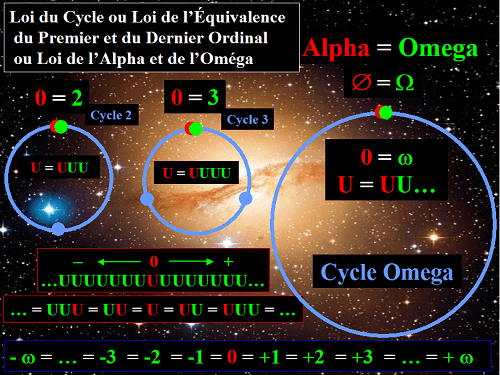
Dans ce paradigme, le Premier Ordinal est aussi le Dernier Ordinal. Les deux sont équivalents:
Ensemble Vide = Ensemble Plein, ou : Ø = Ω ou : 0 = ω ou: Alpha = Omega
(pour plus de détails sur la question, voir l'analyse du Paradoxe de Russell
et du Paradoxe de Burali-Forti).
La notion d'INFINI dans le paradigme de l'Equivalence et du Cycle
Comme vu plus haut dans la présentation générale de la notion d'ordinal et de cardinal,
on appelle nombre entier INFINI ou Oméga, et on le note ω,
tout simplement la générescence UUUUUUU...,
où l'Unit U est répété indéfiniment.
Numériquement, cela revient simplement à dire:
{0, 1, 2, 3, 4, 5, 6, 7, ...}
De très nombreuses notions sont simplement des facettes d'une seule et même notion, celle d'INFINI.
Certaines notions
(comme par exemple les notions de Variable,
d'Equivalence, de Cycle, etc.)
n'ont apparemment aucun lien avec celle d'Infini, et pourtant on parle bien de la même chose.
Dans le nouveau paradigme, les phrases suivantes sont équivalentes:
a) ω est la générescence UUUUUUU...;
b) ω est le Dernier Ordinal ;
c) ω est le nombre entier naturel plus grand que lui-même;
d) ω est le nombre entier naturel infini;
e) ω est un nombre entier naturel aussi grand que l'on veut;
f) ω est un nombre entier naturel indéfiniment grand,
ce qui signifie que tout en restant un nombre entier naturel, il est toujours supérieur
à tout entier naturel fixé à l'avance. On dit aussi qu'il est un infini dynamique;
g) ω est le cycle d'un nombre entier naturel W donné;
ce cycle s'écrit alors: 0 = W ou ω = W.
Autrement dit simplement, ω est le cycle W; il signifie
que l'on répète indéfiniment ce cycle:
0 = W = 2W = 3W = 4W = 5W = ....
Le nombre W est appelé l'Infini du cycle et le nombre 1/W
est appelé le Zéro du cycle;
h) ω est le nombre entier naturel variable
(au sens le plus général) ou entier natuel variable supérieur ou égal à
un nombre entier naturel très grand Z fixé à l'avance, comme par exemple
Lhorizon 3 ou Zhon
(au sens plus restreint, qui signifie donc "nombre entier variable très grand");
L'équivalence: ω = Z
est appelée une définition de l'Infini.
Le nombre 1/Z est appelé un Epsilon ou Zéro défini ou un Infiniment petit.
Il est appelé aussi l'erreur ou la fausseté de la définition,
et le nombre 1 - 1/Z ou (Z - 1)/Z
est appelé la véracité de la définition;
- Etc.
La dernière forme de la notion d'Infini, h), est particulièrement importante.
Cette conception de l'Infini traduit le fait courant et pratique selon lequel nous considérons un nombre comme INFINI
quand il est suffisamment grand de notre point de vue.
Pour l'un, 1000 c'est déjà l'Infini. Pour un autre, 1000 est riquiqui comme Infini,
et qu'à partir de 1000000 ou un million, on peut commencer à parler d'Infini.
Pour un autre encore, cette notion commence à partir de un milliard,
et pour un autre à partir de un milliard de milliards de milliards, etc.
Et nous pouvons convenir que 101000 (ou "10 puissance 1000" ou le nombre décimal écrit avec 1 suivi de mille zéros)
est terriblement grand (et il l'est!), au-delà de notre entendement (et c'est le cas!),
si grand donc qu'à partir de là nous pouvons à bon droit parler d'Infini!
A plus forte raison si le nombre considéré est
1010 000 000 000 ou "10 puissance dix milliards" ou le nombre décimal écrit avec 1 suivi de dix milliards de zéros...
Courage pour écrire tout ça, et surtout pour compter jusqu'à ce nombre!
Ce nombre est ce que nous appelons Lhorizon 3 ou le Zhon
(prononocer "Jonne"; voir ci-après).
Son inverse, 1/Zhon, nous l'appelons le Shon (prononocer "Chonne").
Le Zhon est donc un nombre infiniment grand
et son inverse le Shon est un nombre infiniment petit.
Et c'est plus vrai encore avec Lhorizon 4, de Lhorizon 5, etc.!
Les nombres comme Lhorizon 3 ou Zhon,
et plus généralement tout nombre Infiniment grand, oui les nombres comme
Lhorizon 77, Lhorizon 1000,
Lhorizon 1000000, etc., jouent un rôle extrêmement important
dans l'Univers, en très étroite relation avec la notion de
générescence et de structure fractale,
avec la notion information unaire,
le matériau fondamental de l'Univers!
Leur importance est immense en physique, et en particulier
en physique quantique!
Et pourtant, cette importance a été ignorée jusqu'ici.
La preuve: dans les mathématiques actuelles qui fonctionnent
avec la Logique clasique (mais ce que nous appelons une Logique Négative),
une logique tranchée, grossière, pour tout entier naturel Z donné,
la phrase "Z est l'Infini" ou, ce qui revient au même, l'égalité "1/Z = 0"
sera considérée comme toujours fausse, sans autre forme de procès, sans aucune nuance!
Or il est évident que la fausseté en question de la phrase n'est pas du tout la même chose si
le Z dont on parle est 10 que s'il est 1000000000,
Dans une logique plus fine, plus nuancée, la fausseté est de 1/10 pour 10
(donc la véracité de 9/10), et la fausseté est de 1/1000000000 (0.000000001)
pour 1000000000 et la véracité de 999999999/1000000000 (ou 0.999999999).
Donc cette phrase dite seulement fausse en Logique classique, est ce qu'il faut appeler une phrase
pratiquement vraie ou pragmatiquement vraie!
A plus forte raison si le nombre Z est 101000
et plus encore si l'on parle d'un nombre titanesque comme
Lhorizon 3 ou Zhon!
Dire qu'il est infini c'est dire une phrase dont la fausseté est
de 0.0000... Courage pour écrire tous les 0 avant de mettre la dernière décimale qui est 1!
Et la véracité de cette phrase est de 0.9999.... Et là encore,
courage pour aligner tous les 9!
Et puis, n'oublions surtout pas que nous sommes maintenant dans le
paradigme de l'équivalence
et du cycle,
le paradigme où l'on dit désormais 0 = 1, 0 = 1, 0 = 2, etc.
Il faudra vite s'y habituer,
mettre au plaquard les vieux mécanismes du paradigme de l'identité,
et acquérir les nouveaux automatismes de raisonnement!
Dans le nouveau paradigme, on dit donc 0 = 1,
et à plus forte raison 0 = 0.00000....
De même on ne pinaille plus pour dire 0.9999999.... = 1,
et donc que la véracité de l'idée que Lhorizon 3 est infini est tout simplement 1!
Une égalité comme 0.9999999.... = 1 n'est pas une approximation
avec une "marge d'erreur faible", au sens actuel des termes.
Mais il s'agit tout simplement de vérités du paradigme du cycle et de l'équivalence.
Pour généraliser tout ce que nous venons d'expliquer,
disons simplement que l'équivalence entre l'infini absolu, ω et l'infini grand Z,
à savoir donc ω = Z, est d'importance capitale dans le nouveau paradigme.
A cette équivalence est donc associée une valeur de vérité et de fausseté (ou d'erreur),
qui sont respectivement (Z - 1)/Z et 1/Z.
Comme nous l'avons déjà dit, il ne s'agit pas d'une "erreur" ou d'une "incertitude" aux sens
négatifs actuels de ces termes,
mais des notions positives,
celles de l'équivalence et du cycle, celle de la Logique Alternative,
dans laquelle la vérité est graduelle, nuancée et très fine,
et non pas grossière, tranchée.
Une erreur parfaitement définie, maîtrisée, faite en connaissance de cause, n'est plus une erreur!
Une fausseté parfaitement intégrée comme une chose normale n'est plus une fausseté.
Un dérapage parfaitement contrôlé, qui fait partie du scénario comme un cascadeur au cinéma, n'est plus un dérapage.
Un aléatoire parfaitement calculé n'est plus un aléatoire, un hasard parfaitement déterniné n'est plus un hasard.
Un mal qui fait partie intégrante du programme du bien n'est plus un mal.
Une négation absolue qui fait désormais partie de l'alternation n'est plus une négation absolue.
Un rien qui désormais n'est pas que rien mais est toujours quelque chose, eh bien n'est pas que rien,
et on peut donc désormais faire des choses très intéressantes avec ce rien-là, des choses miraculeuses!
Un zéro qui désormais n'est pas que zéro mais est désormais toujours une quantité,
eh bien, n'est pas que zéro, donc désormais on peut diviser par zéro,
et on entre dans une nouvelle dimension!
Un infini qui n'est plus indéfini mais parfaitement défini par une
équivalence de la forme ω = Z,
cet infini, eh bien, n'est plus indéfini... Et ça change tou! Etc.
Les nombres Horizons: les nombres entiers naturels à la fois FINIS et INFINIS!
Les nombres Infiniment grands et Infiniment petits.
Le nombre Zhon ou Lhorizon 3, et son inverse le Shon...
Définissions maintenant des nombres extraordinairement grands, qui vont très vite dépasser notre entendement dès les tous premiers d’entre eux,
comme par exemple Lhorizon 3 dont nous avons déjà parlé plus haut.
Ce sont donc les infiniment grands.
On définit les nombres Lhorizon de la manière suivante:
Lhorizon 0 = 1
Lhorizon 1 = 101 = 10
Ce nombre s’obtient en écrivant 1 suivi d’un nombre de zéros indiqué par
Lhorizon 0 donc 1 suivi d’un zéro, ce qui donne donc 10 ou « dix puissance 1 ».
Lhorizon 2 = 10Lhorizon 1 = 1010 = 10 000 000 000
Il est obtenu en écrivant 1 suivi d’un nombre de zéros indiqué par Lhorizon 1
donc 1 suivi de dix zéros, ce qui donne donc 10 000 000 000 ou dix milliards, qui est le nombre « 10 puissance 10 ».
Lhorizon 3 = 10Lhorizon 2 = 1010 000 000 000.
ce nombre, nous l'appelons le Zhon (prononcer "Jonne").
L'inverse du Zhon, le nombre 1/Zhon, nous l'appelons le Shon
(prononcer "Chonne").
Le Shon est donc 10-10 000 000 000.
Ce nombre consiste à écrire dix milliards de zéros, à mettre une virgule après le premier et à écrire 1 après le dernier.
Autrement dit, il est de la forme 0.000000...0001, avec dix milliards de chiffres après la virgule,
le dernier chiffre étant 1 et les autres étant des 0.
Et pour un nombre entier n quelconque, on a:
Lhorizon (n + 1) = 10Lhorizon n
qui est donc le nombre qui s'écrit avec 1 suivi d'un nombre de zéros donné par Lhorizon n.
Le dernier Lhorizon est Lhorizon ω. Il obéit donc à la formule finale:
Lhorizon (ω + 1) = 10Lhorizon ω
Il faut maintenant préciser que le mot Lhorizon est constitué du mot Horizon
et de la lettre L indiquant qu'on travaille en base 10.
La table des bases est la suivante:

Les bases sont les consonnes issues de l'ABECIDO,
l'Alphabet cyclique du Verba, un Alphabet 40.
A part les bases spéciales O, U et Z, une consonne en tant que base
est son numéro d'ordre divisé par 2 (car il est pair) auquel on ajoute 1.
Ainsi par exemple, le L est la lettre 18. Donc, comme base, on a L = 18/2 + 1 = 10.
Ainsi, pour base B ou 2:
Bhorizon 0 = 20 = 1
Bhorizon 1 = 2Bhorizon 0 = 21 = 2
Bhorizon 2 = 2Bhorizon 1 = 22 = 4
Bhorizon 3 = 2Bhorizon 2 = 24 = 16
Bhorizon 4 = 2Bhorizon 3 = 216 = 65 536
Etc.
Pour base C ou 3:
Chorizon 0 = 30 = 1
Chorizon 1 = 3Chorizon 0 = 31 = 3
Chorizon 2 = 3Chorizon 1 = 33 = 27
Chorizon 3 = 3Chorizon 2 = 327 = 7 625 597 484 987
Etc.
Pour base D ou 4:
Dhorizon 0 = 40 = 1
Dhorizon 1 = 4Dhorizon 0 = 41 = 4
Dhorizon 2 = 4Dhorizon 1 = 44 = 256
Dhorizon 3 = 4Dhorizon 2 = 4256 = 1,340 780 792 994 259 709 957 402 499 82... x 10154
Etc.
Pour base F ou 5:
Fhorizon 0 = 50 = 1
Fhorizon 1 = 5Fhorizon 0 = 51 = 5
Fhorizon 2 = 5Fhorizon 1 = 55 = 3 125
Fhorizon 3 = 5Fhorizon 2 = 53 125 = 1,911 012 597 945 477 520 356 404 559... x 102 154
Etc.
Les nombres gigantesques de la série Lhorizon sont du néant comparés aux nombres que l'on peut définir avec les hyperopérateurs.
Ceux-ci admettent plusieurs variantes de définition;
dans le langage des générescences ou des informations unaires, nous les appelons les opérateurs HENER.
Voici comment nous les définissons:
H0 ou + : Addition (HENER d'ordre 0)
H1 ou x : Multiplication (HENER d'ordre 1)
H2 ou ^ : Exponentiation (HENER d'ordre 2),
une flèche de Knuth (Wikipédia)
H3 ou ^^ : Tétration (HENER d'ordre 3),
deux flèches de Knuth
H4 ou ^^^ : Pentation (HENER d'ordre 4),
trois flèches de Knuth
H5 ou ^^^^ : Hexation (HENER d'ordre 5),
quatre flèches de Knuth
Etc.
Propriété générale des hyperopérateurs (ou opérateurs HENER):
m Hp 1 = m;
m Hp+1 (n+1) = m Hp (m Hp+1 n),
ou plus simplement:
m Hp+1 n = m Hp ... Hp m Hp m Hp m Hp m,
où m est écrit n fois.
Par exemple la tétration 10 H3 5 (ou 10 ^^ 5) se décompose
comme une chaîne de puissances H2 (ou ^^) suivante:
10 H3 5 = 10 ^^ 5
= 10 H2 10 H2 10 H2 10 H2 10
= 10 ^ 10 ^ 10 ^ 10 ^ 10, où 10 apparaît 5 fois.
et on calcule les puissances de droite à gauche.
Le résultat d'un tel calcul est le nombre que nous avons appelé Lhorizon 5 plus haut ou 10 ^ (10 ^ (1010000000000)).
Avec les hyperopérateurs,
les nombres comme 10 H10 10 ou 7 H7 7
sont fantastiquement colossalement titantesques! Ils sont pour ainsi dire "infinis", et pourtant bien finis.
Et malgré leur grandeur vertigineuse hors de notre entendement actuel,
ils sont pourtant des néants comparés
au Nombre de Graham (Wikipédia),
lui-même infiniment loin d'être ce qu'on peut définir comme nombres colossaux, c'est-à-dire
comme généresences (ou informations unaires) colossales.
Nous qualifions cette conception de l'Infini (et aussi du Zéro),
de générescente,
de fractale,
de cyclique, d'équivalencielle, etc.,
et aussi de concrète,
de physique, de réelle, d'universelle (c'est-à-dire celle de l'Univers TOTAL).
C'est la bonne conception de l'infini, avec elle l'INFINI
entre vraiment en science, pour jouer pleinement qu'il n'a jamais vraiment joué jusqu'ici.
Le très classique et vieux problème de la division par 0,
l'idée selon laquelle 1/0 n'est pas défini,
qu'il ne peut pas exister une algèbre des corps ou une algèbre des nombres réels ou
complexes dans laquelle l'"élément neutre pour la loi addititive" (en clair le 0)
"ne peut admettre un symétrique pour la loi multilplicative" (en clair il est impossible de
diviser par 0, de calculer avec un nombre infini
exactement comme avec les autres nombres), et l'idée en physique selon laquelle l'infini n'a aucune réalité physique
(comme le déclare par exemple l'astrophysicien Christian Magnan),
etc., signifie simplement que même si les sciencse actuelles parlaient jusqu'ici de l'INFINI,
celui-ci n'était pas vraiment dans ces sciences!
L'Infini était très mal conçu, et par conséquent aussi le Zéro, qui était orphelin de ne pas avoir son invserse pleinement dans les sciences.
L'Alpha (le Zéro) était sans son Oméga (l'Infini).
C'est l'Univers TOTAL qui manquait tout simplement ainsi à la science.
En d'autre termes, DIEU manquait en science!
Et maintenant arrive la bonne conception aussi bien du Zéro comme de l'Infini,
de l'Alpha comme de l'Oméga (Révélation ou Apocalypse 1: 8; 21: 6: 22: 13).