Générescence et codage de toutes choses

Le HENER et le GENER: les opérateurs fondamentaux de la générescence

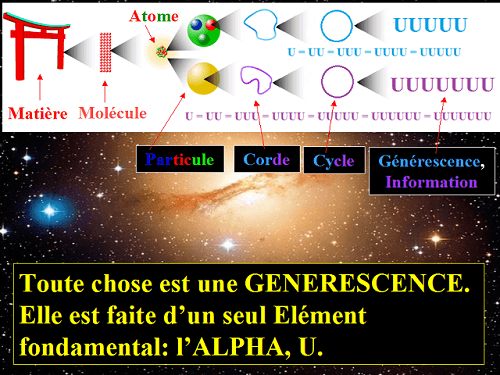
Le but du présent document est de détailler l'un des aspects du document Générescence et Structure FRACTALE: "Toute chose est une information constituée d'une UNIQUE information fondamentale: l'Univers TOTAL, U (voir aussi les documents Théorie physique des ensembles, nouvelle Science de la Matière et Physique Quantique de l'Univers TOTAL, la Physique du TOUT).

L'Univers TOTAL: l'Unit, l'Unité universelle, la plus petite et la plus grande INFORMATION

L'opérateur HENER: l'opérateur des modèles, l'opérateur Point, l'opérateur Version

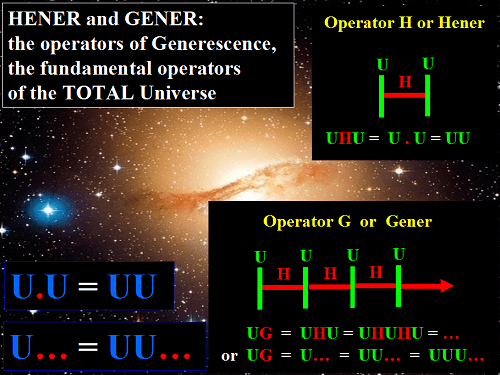
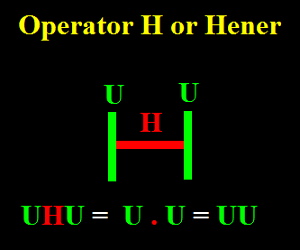
L'opérateur Hener ou opérateur H, noté ".", est l'opérateur le plus fondamental de l'Univers TOTAL. Il assemble deux units U pour former la générescence UU. Selon le contexte ou l'angle sous lequel il est vu, ce très important opérateur est appelé:
- opérateur de Constitution physique (car il est l'opérateur de formation des ensembles physiques et des ensembles quantiques),
- opérateur de Concaténation (l'opérateur d'assemblage de l'information, des lettres, des mots, etc.),
- opérateur Espace ou opérateur Intervalle (de par sa nature même d'être l'espace ou l'intervalle entre les choses qu'il assemble, il sépare ces choses et les unit à la fois!),
- opérateur de Vide ou le Vide (étant donné qu'il incarne le "Vide" séparant deux Units; il est alots noté Ø),
- opérateur Point (comme par exemple quand on dit "hubertelie.com" ou "hubertelie point com"),
- opérateur de Modèle ou opérateur de Version (opérateur très important du langage des modèles, notion fondamentale dans le langage de la générescence et de la structure fractale. Cet opérateur permet de créer ou de générer de nouveaux modèles à partir de modèles déjà crées, et aussi de parler des versions de modèles),
- opérateur d'Addition (car les générescences qu'il assemble sont des nombres et il additionne simplement ces nombres; cet opérateur est la définition la plus fondamentale de l'Addition; l'opération de base qu'il fait, U.U = UU est tout simplement 1 + 1 = 2! Il est pour cela l'opérateur arithmétique fondamentale),
- opérateur de Commposition ou opérateur de Multiplication sémantique (car tout en additionnant physiquement les informations, il compose leurs sens, il multiplie les sens pour former un nouveau sens. Par exemple, il compose le sens U et de U pour former le sens UU. C'est l'opérateur sémantique fondamental, de la sémanthmétique ou arithmétique du sens, l'opérateur même du Verba, le Langage de l'Etre, le Langage universel des ensembles. C'est l'opérateur linguistique fondamental),
- Etc.

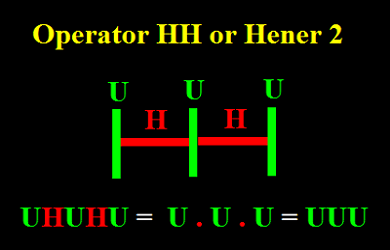
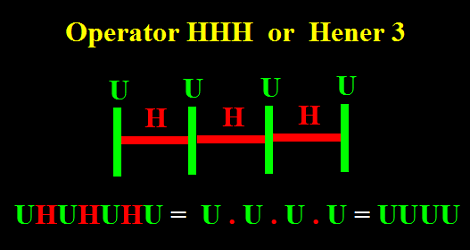
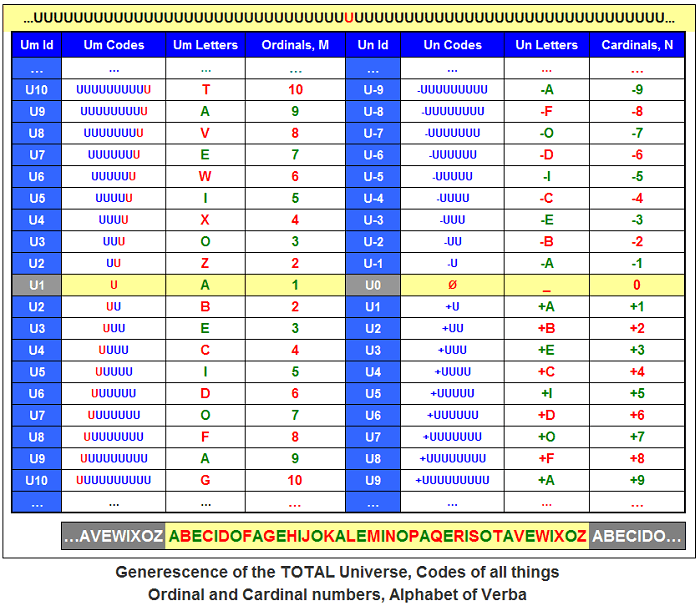
On voit facilement que la relation entre l'Unit U et le Hener H est une affaire de poteaux et d'intervalles. Il est clair qu'on peut intervertir les rôles, prendre les Heners ou les H pour les informations, et alors les Units ou les U deviennent les intervalles entre les informations. Autrement dit, le Hener H n'est autre que l'Unit U dans un autre rôle. Les Units U sont la définition aturelle des nombres ordinaux et les Heners H sont la définition naturelle des nombres cardinaux.

L'opérateur GENER: l'opérateur de la Génération, de la Reproduction indéfinie

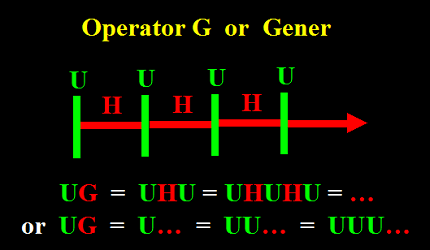
La répétition indéfinie de l'opérateur Hener donne un nouvelle opérateur appelé le Gener ou opérateur G. Il est aussi appelé l'opérateur de Génération (du verbe générer) ou opérateur de Reproduction ou de Répétition indéfinie. Il est noté aussi "...", et il est la définition la plus fondamentale des fameux "trois points". Appliqué à un modèle ou simplement à une chose M donnée, il signifie qu'il faut répéter indéfiniment M du côté où se trouve l'opérateur.

Par exemple, M G ou M... signifie qu'il faut répéter M indéfiniment vers la droite: MMMMMMMMMMMM.... Et en pratique, comme on est obligé de s'arrêter après un certain nombre de répétitions, il faut alors mettre le Gener ou "..." après la dernière répétition, pour dire que la répétition continue. Autrement dit, on a la chaîne d'égalités suivantes:
M G = M... = MM... = MMM... = MMMM... = MMMMM... et ainsi de suite.

Et de même, G M ou ...M signifie qu'il faut répéter M indéfiniment vers la gauche: ...MMMMMMMMMMMM.

Et plus généralement, le modèle M est répété dans la direction indiquée par le Gener, et éventuellement dans plusieurs directions, comme par exemple la répétition dans les deux directions gauche et et droite: G M G ou ...M..., qui veut dire donc ...MMMMMMMM...

Un usage très important du Gener et de de lui associer un nombre infiniment grand W comme par exemple 10^{10 000 000 000} ou Lhorizon 3 ou Zhon. Et alors l'opérateur Gener signifie qu'il faut répéter le modèle M un nombre de fois égal à W.

La construction par récurrence de toutes les générescences, les codes de toutes les choses;
La définition informatique de l'Univers TOTAL, de l'Univers Générescent et Fractal.

Les très classiques parenthèses "(" et ")" sont aussi des opérateurs de la générescence, de la famille des IDENER ou "Opérateurs d'Identité", les opérateurs dont le rôle est d'indiquer ce qui doit être pris en bloc comme comme une seule unité, comme l'Unit U. Autrement dit, tout ce qui est entouré de parenthèses est à considérer et à traiter comme si c'était l'Unit.

Les opérateurs sont ni plus ni moins des générescences aussi, mais simplement dont on ne précise pas la structure, mais qui servent à indiquer la structure des autres générescences. On les appelle des méta-générescences.

La définition de l'Ensemble de toutes les générescences

On définit ou plutôt construit les générescences ou les informations unaires avec les règles suivantes:
1) L'unit U est une générescence;
2) Si X et Y sont des générescences, alors X.Y est une nouvelle générescence;
3) Si X est une générescence, alors (X) est une nouvelle générescence;
4) Si X est une générescence, alors X... et ...X sont de nouvelles générescences;
5) Toutes les générescences ou informations sont obtenues par appplication répétée des quatre règles précédentes.

Les générescences ou informations que nous venons de définir sont ce que nous appelons les choses, les ensembles. L'ensemble de ces informations constitue la plus grande information qui soit, qui est la définition informatique de l'Univers TOTAL. Cette grande information est notée notée UT, comme "Univers TOTAL". Et c'est cette infirmation qui est donc aussi la plus petite information, U, l'Unit, l'information élémentaire qui sert à construire toutes les autres.

L'équivalence entre UT et U, c'est-à-dire U = UT, est l'expression de la structure fractale de l'Univers TOTAL, la traduction informatique de cette vérité:

"L'Univers TOTAL, U, est l'Ensemble de toutes les choses. Mais l'Univers TOTAL est lui-même une chose, donc il est un élément de lui-même. Il est donc à la fois l'Ensemble (donc le dernier des ensembles, le plus grand), noté alors UT; et il est à la fois l'Elément (donc le premier des éléments, le plus petit d'entre eux), noté alors U."

Cas particuliers de générescences importantes: génerescences U_1D, U_2D, U_3D, etc

La générescence U... est appelée le Genit ou l'Oméga, et est notée Ω ou en minuscule ω. Et la générescence ...U est appelée le Negit ou Anti-Genit ou simplement l'Anti-Oméga, notée -Ω. La générescence ...U... est appelée la générescence U_1D ou la générescence infinie de dimension 1, qui est la définition informatique de la Droite.

La générescence ...(U_1D)... est appelée la générescence U_2D ou la générescence infinie de dimension 2, qui est la définition informatique du Plan.

Et en faisant le même chose avec la générescence U_2D, on obtient la générescence U_3D ou la générescence infinie de dimension 3, qui est la définition informatique du Cube infini ou espace en trois dimensions, etc.