La Négation Absolue: la vraie cause de tous les Paradoxes

Sommaire du sous-titre

• - L'Univers TOTAL le contexte par excellence où toute vérité coexiste avec son contraire.
• - Le Paradoxe de Russell ou Paradoxe de l'ensemble des ensembles non-auto-appartenants
• - Le Paradoxe de Burali-Forti ou Paradoxe de l'Ensemble de tous les ordinaux ou Paradoxe du Dernier ordinal
• - Le Paradoxe Sorite ou Paradoxe de X et Non-X ou Paradoxe de la Ségrégation ou Paradoxe de la Frontière

L'Univers TOTAL le contexte par excellence où toute vérité coexiste avec son contraire.

Tous les paradoxes de la théorie des ensembles et des sciences en général ont une seule cause ignorée jusqu'ici: la négation absolue, le fait de dire qu'une chose n'existe pas, n'est pas vrai ou est impossible dans l'Univers (voir L'Axiome de Non-Existence: le plus fondamental et le plus vicieux de tous les paradoxes). Quand une chose est ainsi niée de manière absolue, elle ne laisse la place à la véracité, à la réalité ou à l'existence de son contraire. 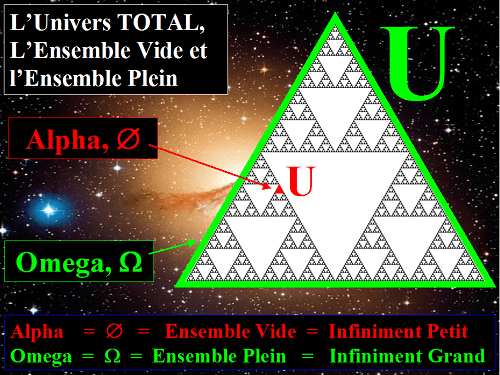L'Univers TOTAL le contexte par excellence où toute chose coexiste avec son contraire, toute vérité coexiste avec son contraire. C'est pourquoi une chose comme l'Univers TOTAL ou les ensembles qui sont équivalents à l'Univers TOTAL est l'objet paradoxal par excellence selon la négation absolue. Mais le vrai paradoxe est tout simplement cette négation.

Dans la classique théorie axiomatique des ensembles (celle de Zermelo-Fraenkel ou ZF), un problème (dû à la négation absolue donc) se pose avec l'ensemble de tous les ensembles qui n'est qu'une autre façon de parler de l'Ensemble de toutes les choses, à savoir donc l'Univers TOTAL. Plus indirectement, on a le Paradoxe de Russell (qui concerne l'ensemble de tous les ensembles non-auto-appartenants) ou le Paradoxe de Burali-Forti (qui concerne l'ensemble de tous les ordinaux ou Dernier ordinal).

Le Paradoxe de Russell ou Paradoxe de l'ensemble des ensembles non-auto-appartenants

Le paradoxe de Russell est le problème suivant: "Un ensemble A a pour éléments les ensembles non-auto-appartenants, c'est-à-dire qui ne sont pas éléments d'eux-mêmes. La question est de sa voir si cet A appartient ou non à lui-même."

Si A appartient à lui-même, alors il est un des ensembles qui n'appartiennent pas à eux-mêmes, puisque par définition il est l'ensemble justement de tels ensembles. Donc il n'appartient pas à lui-même... Mais s'il n'appartient pas à lui-même, il répond exactement à la définition de ses éléments, donc il est l'un d'eux, donc il appartient à lui-même. D'où le paradoxe.

Plus schématiquement, l'ensemble A est défini par l'équivalence logique suivante:

X ∈ A <=> X ∉ X
(lire "X apprtient à A si et seulement si X n'appartient pas à X)

Donc, pour répondre à la question concernant A lui-même, il faut remplacer X par A dans l'équivalence, et cela donne:

A ∈ A <=> A ∉ A
(lire "A apprtient à A si et seulement si A n'appartient pas à A)

C'est donc cela qu'on a appelé le célèbre Paradoxe de Russell. Et un objet mathématique ou scientifique qui donne lieu à ce genre d'équivalence logique entre un énoncé et son contraire est qualifié de paradoxal ou de contradictoire dans la logique scientifique actuelle. Mais le problème est simplement que l'on fonctionne dans des paradigmes trop étroits pour traiter de nombreux objets et situations de l'Univers TOTAL, à commencer par l'Univers TOTAL lui-même. On travaille dans le paradigme de l'Identité, on fait la science avec la négation absolue, on raisonne avec une logique négative, c'est-à-dire qui repose sur le principe de non-contradiction d'Aristote (un mauvais principe de non-contradiction, le bon principe étant la Loi de Séparation et d'Union des contraires).

C'est dans le paradigme de l'Equivalence qu'il faut faire la science. On travaille alors avec une négation relative que nous appelons l'alternation, et la logique qui y correspond est la surpuissante logique alternative ou logique cyclique. Dans ce paradigme, l'ensemble A est un exemple d'objet que nous appelons un objet alternatif.

Un objet est alternatif:
- s'il présente deux aspects contraires, comme par exemple le côté Pile et Face d'une même pièce de monnaie;
- s'il est un système où il se produit aussi bien les événements que les événements contraires, ce qui est le cas de l'Univers où Il pleut par exemple ici et Il ne pleut pas ailleurs, où la Pluie et le Beau temps alternent dans l'espace et dans le temps;
- ou s'il est tout simplement un objet dynamique!

Voici maintenant un très important autre exemple d'objet alternatif: que l'on regarde le très pédagogique Triangle de Sierpinski, une structure fractale. Il a une logique qui est tout simplement l'une des infinités de solutions (les vraies!) au prétendu Paradoxe de Russell:

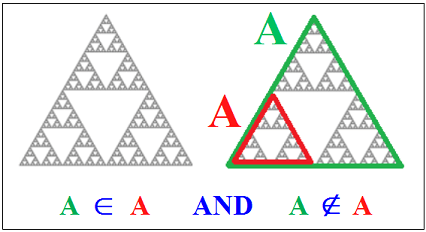
On a ici deux versions du seul et même Triangle de Sierpinski appelé A, le grand (vert) et le petit (rouge). A appartient à lui-même au sens de l'Equivalence (conception très large de l'égalité très fondamentale en logique fractale ou cyclique), car le grand modèle et le petit modèle sont équivalents. Mais A n'appartient à lui-même au sens de l'Identité (conception très restreinte de l'égalité, la conception actuelle, étroitement associée au problème de la négation absolue), car que ce soit le petit modèle ou le grand modèle, il n'est pas plus petit que lui-même, mais juste identique à lui-même. Autrement dit, il n'y a pas de version du petit modèle (comme aussi du grand modèle) qui soit strictement à l'intérieur de lui-même. Il existe des modèles strictement à l'intérieur, mais ils sont évidemment plus petits. Si donc l'on ne raisonne qu'en terme d'Identité, seule la non-appartenance est vraie ici, donc c'est un paradoxe de dire que l'apprtenance est vraie aussi. Mais si l'on raisonne en terme d'équivalence, les deux deviennent vrais.

C'est l'un des exemples qui montre que c'est l'étroitesse du paradigme (celui de l'identité) qui engendre le paradoxe, et non pas le fait que d'un point de vue logique les deux contraires ne peuvent pas être vrais. Il existe tout à fait des logiques (ici la logique fractale) où les deux contraires sont vrais sans qu'il y ait le moindre paradoxe. Autrement dit, la négation "A N'APPARTIENT PAS...", "A N'EXISTE PAS...", et plus généralement tout simplement "A N'EST PAS...", est absolue dans le paradigme de l'Identité, car il n'existe aucune possibilité que son contraire "A APPARTIENT...", "A EXISTE...", "A EST...", soit vraie aussi. Mais dans la paradigme de l'Equivalence, cette alternative existe toujours, ce qui fait que la négation est juste relative.

Une forme populaire du Paradoxe de Russell est le Paradoxe du barbier: "Le barbier d'un village nommé Antoine (abrégé A) rase tous les hommes du villages qui ne se rasent pas eux-mêmes. Est-ce que ce barbier A se rase à lui-même?"

Ici aussi, un raisonnement simple permet de voir que si si l'on dit oui, alors on doit dire non, et si l'on dit non, alors on doit dire oui. Comme pour le Triangle de Siperpinski où le problème est simplement résolu en considérant deux rôles ou deux versions du même objet qui entretiennent entre elles une relation d'équivalence (chaque version ne pouvant entretenir qu'une relation d'identité avec elle-même), ici aussi il faut simplement distinguer deux rôles du même Antoine: le barbier et le citoyen ordinaire du village. En tant que citoyen, il ne se rase pas lui-même mais a besoin du barbier, et en tant que barbier il se rase pas lui-même. Cela n'est pas paradoxal au sens d'une impossibilité logique, mais cela est paradoxal au sens simplement que deux aspects contraires se trouvent réunis dans une même personne ou dans une même chose.

On peut en tant que citoyen payer certains frais comme tout le monde, enregistrés par le service adéquat (par exemple le frais de carburant payés à la station service), mais en tant que privilégié se voir rembourser ces frais par un autre service (son patron, les services fiscaux ou autre). Donc on paie, et finalement on ne paie pas. On ne paie pas, mais finalement on paie.

Contrairement à la manière dont les choses ont été conçues jusqu'ici et en particulier à la manière dont la logique fut pratiquée, une équivalence logique entre un énoncé et son contraire n'est pas nécessairement un paradoxe, ou le fait qu'une chose et son contraire soient vraies toutes les deux!

Pour reprendre la situation d'Antoine le barbier du village, ajoutons le problème suivant: Antoine a l'habitude de jouer aux échecs seul, c'est-à-dire contre un aversaire qui est lui-même. Il joue son coup avec les blancs, puis passe de l'autre côté de l'échiquer pour jouer son coup avec les noirs, etc. Et Antoine dit: "Si je gagne la partie, alors je perds la partie; et si perds la partie, alors je gagne la partie". Voilà une sitation qui est un paradoxe de type Russell si l'on raisonne avec logique l'identité seule. Mais ici comme dans les autres exemple, il y a un objet qui a deux rôles ou deux versions, qui entretiennent de ce fait une relation d'équivalence. Au sens de l'identité il est impossible de gagner et de perdre en même temps, mais au sens de l'équivalence c'est possible: on gagne sous un rôle, et on perd de ce fait sous l'autre rôle et vice-versa.

Le Paradoxe de Burali-Forti ou Paradoxe de l'Ensemble de tous les ordinaux ou Paradoxe du Dernier ordinal

Le Paradoxe de Burali-Forti est celui de l'ensemble de tous les ordinaux. Un ordinal (dans la conception classique de la notion, car cette notion, comme celle de cardinal, se simplifie considéralement dans le paradigme de l'Univers TOTAL) est la généralisation de la notion d'entier naturel. Dans la conception classique ( le paradigme de l'Identité), un ordinal est non-auto-appartenant (il n'est pas élément de lui-même), ce qui complique inutilement les choses. Mais il est à la fois auto-appartenant et non-auto-appartenant dans le paradigme de l'Equivalence (exactement comme la fractale de Sierpinski vue ci-dessus), ce qui simplifie considérabement les choses.

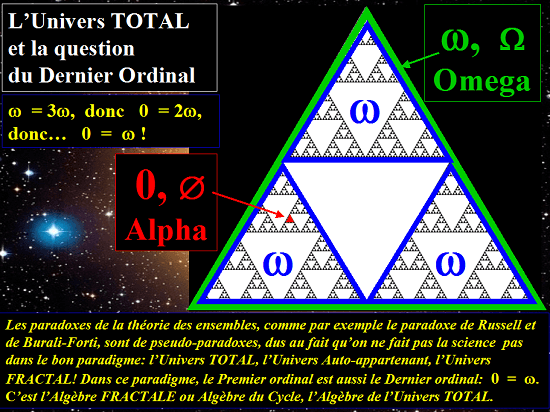
Dans la conception classique, pour un ordinal α (lire "alpha minuscule"), on a donc seulement cette vérité:
α ∉ α (à lire donc "α n'est pas un élément de α")

Et dans la conception classique comme dans la nouvelle, l'ensemble de tous les ordinaux, appelons-le ω (lire "oméga minuscule"), doit être lui-même un ordinal, et alors il est le plus grand de tous, le dernier, puisqu'il est leur ensemble.

Mais c'est là où le problème se pose avec la conception classique, le paradigme de l'Identité. Ce qui pose problème est exactement qu'il soit un ordinal. En effet, étant l'ensemble de tous les ordinaux, il est donc un élément de lui-même (ω ∈ ω), puisqu'il est aussi un ordinal. Or il est interdit dans la conception classique des ordinaux qu'un ordinal soit élément de lui-même, il doit obéir uniquement à la loi α ∉ α, c'est-à-dire donc ω ∉ ω. D'où le paradoxe de Burali-Forti.

En réalité, ce paradoxe n'est rien d'autre que le Paradoxe de Russell. C'est parce qu'on fonctionne dans un paradigme ou les notions d'ensemble et d'ordinaux sont séparés (c'est-à-dire où un ordinal est un ensemble mais où un ensemble n'est pas forcément un ordinal) que les deux problèmes apparaissent comme différents. Sinon, ce problème en réalité le même que celui de l'ensemble des ensembles non-auto-appartenants, c'est-à-dire le Paradoxe de Russell. C'est le paradigme de le paradigme de l'Equivalence qui permet de découvrir que les ensembles non-auto-appartenants dont on parle dans le Paradoxe de Russell sont les ordinaux.

Nous avons posé le problème et donné sa solution en même temps. Il faut tout simplement raisonner dans le paradigme de l'Equivalence ou de la Structure fractale, et le problème est résolu, comme nous l'avons illustré dans le diagramme au début de ce sous-titre. ce diagramme montre ω élément de lui-même au sens de l'équivalence. Il ne l'est pas au sens de l'identité seule mais l'est au sens de l'équivalence. Non seulement cela, la logique fractale montre l'équivalence "0 = ω", qui veut dire que le Premier ordinal ou le Vide est aussi le Dernier ordinal ou le Plein. L'Algèbre de l'Equivalence (ou Algèbre de la Structure Fractale ou Algèbre du Cycle) est infiniment plus puissance et plus féconde que l'actuelle Algèbre de l'Identité.

Le Paradoxe Sorite ou Paradoxe de X et Non-X ou Paradoxe de la Ségrégation ou Paradoxe de la Frontière

La Padaoxe Sorite ou Paradoxe de X et Non-X est l'un des paradoxes les plus basiques de la négation absolue mais aussi l'un des plus néfastes dans la société, car la vision du monde en terme de X et Non-X est le fondement même des choses comme la ségrégation, l'une des manifestations les plus basiques de la psyché de Négation.

Le problème est simple: "Si l'on considère que 10 est un petit nombre et que Lhorizon 3 (10^{10 000 000 000} ou "10 puissance 10 000 000 000" ou le nombre écrit avec 1 et dix milliards de zéros derrière) est un grand nombre, alors où s'arrêtent les petits nombres et où commencent les grands? Plus généralement, étant donnée une notions quelconque X, où s'arrête le X et où commence le Non X? Ce type de problème ne se pose plus en Logique alternative ou la vérité est graduée.

En Logique négative, où l'on ne raisonne pas en termes d'équivalence mais toujours en termes d'identité, on ne dit donc jamais des choses comme 0 = 1, qui sont pourtant de simples vérités exprimées par le Cercle.

Dans cette logique aussi, quel que soit le nombre entier naturel n considéré, on dira toujours de la phrase "n est INFINI" (que nous notions "ω = n") qu'elle est FAUSSE, sans autre forme de procès. On dira donc que "10 est INFINI" est faux, que "100 est INFINI" est faux, que "1000 est INFINI" est faux, que "10 000 000 000 est INFINI" est faux, etc.

Or, au fur et à mesure que le nombre n considéré est grand (donc "tend vers l'INFINI" comme on dit actuellement), la phrase "ω = n" (c'est-à-dire "n est INFINI") est évidemment de moins en moins fausse et de plus en plus vraie! C'est ainsi que l'on voit les choses dans le nouveau paradigme.

En Logique alternative donc, on dit simplement que la fausseté de la phrase "ω = n" (ou "n est INFINI") est très exactement de 1/n et que sa véracité est de 1 - 1/n ou (n - 1)/n.

Ainsi:
- "ω = 10" (ou "10 est INFINI") est fausse à 1/10 et vraie à 9/10.
- "ω = 100" (ou "100 est INFINI") est fausse à 1/100 et vraie à 99/100.
- "ω = 1000" (ou "1000 est INFINI") est fausse à 1/1000 et vraie à 999/1000.
- "ω = 10 000 000 000" (ou "10 000 000 000 est INFINI") est fausse à 1/10 000 000 000 et vraie à 9 999 999 999/10 000 000 000.
- Et ainsi de suite..

Et maintenant, considérons comme définition de l'INFINI ω le nombre:
Lhorizon 3 = 10^{Lhorizon 2} = 10^{10 000 000 000}
ou "10 puissance 10 000 000 000", c'est-à-dire le nombre écrit avec 1 suivi de dix milliards de zéros!
Là, la fausseté de la définition est:
1/ω = 1/Lhorizon 3 = 0. 000 000 000 000...
et sa véracité est par conséquent de:
1 - 1/Lhorizon 3 = 0.9 999 999 999 999.... Bref, il faut avoir le courage de mettre tous les 0 et tous les 9!

On peut donc déjà considérer Lhorizon 3 comme une bonne définition de l'INFINI, à plus forte raison Lhorizon 4, Lhorizon 7, Lhorizon 1000, Lhorizon 10000000000000000!

Moralité: la notion d'INIFINI n'avait pas besoin d'être autre chose qu'un nombre fini, mais AUSSI GRAND QUE L'ON VEUT!. C'est la simple et bonne définition de l'Inini dans la Science de l'Univers TOTAL. C'est nous qui décidons si telle définition ou telle autre est satisfaisante ou non. Tout dépend de ce que l'on veut faire. Et à chaque définition correspond une erreur mesurée avec une grand précision, qui est d'autant plus faible que le nombre choisi est plus grand.

Le paradoxe Sorite se cache dans nombre de concepts des mathématiques et des sciences actuelles, considérés pourtant comme des vérités absolues.

Par exemple, il est établi que le nombre pi ou π est un nombre irrationnel, donc la phrase "π est rationnel" ou "π est une fraction est toujours fausse. C'est donc le problème Sorite ici (le problème X et Non-X) sous la forme de la séparation entre Rationnel et Non-Rationnel. Mais en Logique alternative, la question est plus nuancée que cela, exactement pour les raisons présentée ci-dessus.

Il suffit par exemple de mettre à 0 toutes les décimales de π à 0 à partir de la Lhorizon 1000 ème décimale pour obtenir un nombre rationnel q tel que la fausseté de la phrase "π = q est quasi nulle donc sa véracité quasiment 1! L'erreur est en effet de l'ordre de ε = 1 / Lhorizon 1000. Dans le paradigme de l'équivalence où l'on dit 0 = 1, on dit à plus forte raison: 0 = ε! Dans ce paradigme, la phrase "π = q est tout simplement vraie, π est un rationnel!