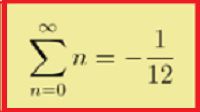Les nombres entiers variables et la bonne conception de l’infini

Dieu a fait les nombres entiers, tout le reste est l'œuvre... du Diable

Voir le livre PDF:
Générescences, Nombres entiers variables,
Corps omégacyclique et Division omégacyclique par Zéro

Je commence par dire ceci: Malgré tout le grand estime que j’ai pour le cher Georg Cantor, le père de la surpuissante théorie des ensembles, je suis obligé de donner un peu raison à son adversaire Leopold Kronecker, quand il dit: "Dieu a fait les nombres entiers, tout le reste est l'œuvre de l'homme". Il a un peu raison, pas totalement, car en fait, le reste est l’oeuvre de la logique de Négation (voir: Problème de la Négation, Paradoxe de la NON-Existence, Théorème de l'Existence, et: Le Principe de Non-Contradiction, le Principe de la Négation de l'Univers TOTAL, ou aussi: Identité et Equivalence, Négation et Alternation), la logique du Diable, dont Kronecker lui-même, Cantor, Hilbert, Euler, Einstein, Gödel, etc., bref tous les mathématiciens et scientifiques sincères de tous les temps, ont été victimes.

Kronecker a dit cela car il rejettait la théorie des cardinaux infinis que Cantor introduisait, et qui aujourd'hui est considérée comme l'une des plus brillantes et importantes innovations mathématiques. C'est effectivement le cas, sauf qu'il y a un bug caché dans cette théorie, comme dans l'ensemble de la théorie des ensembles de Cantor. On a ainsi relevé beaucoup de paradoxes dans cette théorie des ensembles, dont certains célèbres, comme par exemple le paradoxe de Russell (du nom de Bertrand Russell son découvreur) ou encore le paradoxe de Burali-Forti ou paradoxe du dernier ordinal, qui est précisément le problème de l'infini, tel qu'il se pose en théorie des ensembles.

Le pauvre Cantor n'y est pour rien dans tous ces paradoxes ou bugs, car ce sont les paradigmes des mathématiques et des sciences actuelles qui sont bugués, en raison de la logique de Négation avec laquelle on fonctionne. Le grand mathématicien David Hilbert, quand ces bugs ont éclaté et que Kronecker et d'autres y voyaient la preuve que la théorie de Cantor (notamment sa théorie des cardinaux infinis) était fausse, a fait une déclaration restée célèbre aussi dans l'histoire des mathématiques: "Du paradis créé pour nous par Cantor, personne ne nous chassera."

Hilbert proposa de sauver le paradis en fondant la théorie des ensembles (et donc aussi des cardinaux infinis) sur des bases rigoureuses, et la méthodologie axiomatique a la réputation d'être un étalon en matière de rigueur scientifique. Sauf qu'il y a un gros problème que personne n'a vu ou plutôt que ceux qui connaissent vraiment les secrets cachés des paradigmes des sciences actuelles (ce qui visiblement n'est pas le cas ni de Hilbert, ni de Cantor, ni d'aucun des scientifique que j'ai cités jusqu'à présent), ne veulent pas voir. Ce secret est que les paradigmes ont été posés de manière à exclure le vrai infini des mathématiques. Et ce vrai infini est précisément le dernier ordinal ou le dernier cardinal (le Grand Oméga). C'est son absence qui se traduit par le fait que la division par 0 (je parle du zéro absolu, l'élément neutre de l'addition), est "impossible".

Ce problème de la division par 0, qui remonte à l'antiquité des sciences, n'est pas la faute d'aucun des scientifiques mentionnés, mais est la faute de la logique de Négation. Ce n'est même pas la faute d'Aristote qui posa explicitement les principes de cette logique de Négation ( Le Principe de Non-Contradiction, le Principe de la Négation de l'Univers TOTAL).

Il posa ces principes dits de logique classique sans se douter le moins du monde (j'en suis persuadé) que la notion de Négation, qui est centrale dans ces principes et la logique correspondante, est très problématique. En effet, la Négation absolue conduit à nier en sciences le concept d'Univers TOTAL dont nous traitons dans ce site et les blogs associés. Et le concept d'Univers TOTAL, c'est le concept de Réalité TOTALE, d'Etre TOTAL, autrement dit la manière dont la notion d'Etre Suprême, donc de DIEU, se définit en mathématiques et sciences. En langage des ensembles (c'est là où la théorie des ensembles de Cantor est extrêmement importante), sa définiton est: l'Ensemble de TOUTES les choses et de TOUS les êtres, l'Etre TOTAL donc, le Grand TOUT, le Grand Infini, l'Alpha et l'Oméga!

Cet Ensemble Suprême correspond à la notion d'Ensemble de tous les ensembles, qui est concerné par l'un des paradoxes de la théorie des ensembles de Cantor. et en tant que l'Etre INFINI, le Vrai, le Premier et le Dernier, l'Alpha et l'Oméga, l'Unique, il est concerné aussi par le paradoxe de Burali-Forti, mais aussi la question de la division par zéro! Si l'on dit qu'il existe, cela provoque des paradoxes, mais selon la logique classique, celle d'Aristote, qui est donc une logique de Négation. Le problème de paradigme et de fondements des sciences, il est là! Ce n'est donc pas que la notion d'Etre Suprême (et la notion de vrai INFINI, l'INFINI absolu ou Oméga qui lui est synonyme, de même que la notion de ZÉRO absolu ou Alpha) est "impossible" en science, mais c'est simplement un problème de logique scientifique!

Autrement dit, c'est la logique scientifique depuis Aristote (2300 ans environ avant Jésus Christ) à nos jours qui est foireuse pour pouvoir traiter des notions transcendantes (c'est-à-dire toutes les notions synonymes de Dieu), et non pas que ces notions sont scientifiquement "impossibles". Autrement dit encore, c'est la logique de Négation. avec laquelle on travaille depuis la nuit des temps, et notamment depuis ces 2000 ans derniers, depuis le temps de Jésus Christ, l'écriture des évangiles, du livre de l'Apocalypse (où l'on trouve la formule divine: "Je suis l'Alpha et l'Oméga" (Apocalypse 1: 8; 21: 6; 22: 13)), jusqu'à nos jours, qui est foireuse!

Après analyse, il apparaît très clairement que ces paradigmes scientifiques ont été retenus exprès tout au long des 2000 ans écoulés, par les plus grands penseurs successifs des sciences actuelles, pour exclure la question de Dieu en sciences, comme Jésus Christ fut crucifié. Et pour tout dire, ceux qui ont posé ou plutôt imposé ces paradigmes de Négation, ne sont pas nécessairement des scientifiques, les vrais, mais des religieux souvent, des esprits du Talmud et de la Kabbale (c'est-à-dire les successeurs des pharisiens qui ont crucifié Jésus), puis leurs propres acolytes ou infilrés dans le monde chrétien. Notamment dans l'église catholique, pour la corrompre de l'intérieur, et l'empêcher d'accomplir sa vocation d'universalité, de vraie universalité, car le mot "catholique" veut dire simplement "universel".

Et l'Universel ou l'Universalité dont nous parlons, est ni plus ni moins la Science de l'Univers TOTAL dont nous parlons aujourd'hui. C'est cette mission que le Diable, qui avant-hier tuait les prophètes de la Torah, du Tanakh ou Ancien Testament (le fondement du vrai judaïsme, qu'il ne faut plus confondre avec le pharisaïsme dont la forme actuelle est le talmudisme; voir Matthieu 15: 3-9; 23: 13; 29-39), et qui hier a tué Jésus et des apôtres, a ensuite infiltré l'église pour l'empêcher d'accomplir sa mission. La Connaissance de Dieu devrait progressivement se transformer en Science de Dieu, et c'est ce terrain que préparaient des philosophes juifs comme Baruch Spinoza, et nombre de scientifiques souvent juifs dont justement Georg Cantor, Albert Einstein, pour ne parler que d'eux. Sauf que, sans qu'ils le sachent, l'esprit occulte, talmudique et kabbalistique opérait dans l'ombre pour donner à la science l'orientation de Négation du vrai Dieu qu'elle a prise, donc pour qu'elle soit la science du Diable. Autrement dit, une religion, déguisée en science, le SCIENTISME, qui se servait des scientifiques pour atteindre ses buts, tous, sauf scientifiques.

C'est depuis notamment 2020 que cette religion scientiste sort de l'ombre et se révèle maintenant comme le covidisme, l'ukrainisme, le climatisme, le lgbtisme, le transgenrisme, et j'en passe. Et tout cela sous le joug du WEF des Klaus Schwab, des Yuval Noah Harari, Georges Soros, Bill Gates, etc., eux-mêmes n'étant que les représentants de leurs maîtres rothschildiens et rockefelleriens, au sommet de cette pyramide du Diable de plus en plus évidente. Voilà depuis 2000 ans au moins ceux qui faisaient et font les sciences actuelles et leur paradigmes.

Les scientifiques sincères, qui recherchaient uniquement la vérité scientifique et rien qu'elle, faisaient leur travail le plus consciencieusement et cherchaient à résoudre les problèmes qui se posaient, comme par exemple les paradoxes de la théorie des ensembles de Cantor, le problème de la division par zéro, etc. Mais ce n'était pas eux qui décidaient véritablement des paradigmes scientifiques, mais des initiés dans l'ombre. Ils étaient les serviteurs de maîtres cachés qu'ils ignoraient, De temps en temps, quand l'un d'entre eux, par amour simplement de la vérité scientifique, s'aventurait dans des sentiers de découverte qu'ils ignoraient être interdits, la foudre leur tombait sur la tête, sans qu'ils comprennent ce qui leur arrivait, et le mal qu'ils ont pu faire. De nos jours, ce genre de scientifiques s'appellent Didier Raoult, Luc Montagnier, Jacques Benveniste, Christian Perronne, Jean-Bernard Fourtillan, Alexandra Henrion-Caude, Astrid Stuckerberger, etc. La liste est longue, de plus en plus longue, et pardon de ne pas pouvoir tous les citer.

Voilà donc comment marchait la science, les esprits scientistes qui en faisaient une religion qui ne disait pas son nom. Ces esprits sont très reconnaissables à présent, ce sont ceux qui crient à longueur de journée "science! science! science!" mais qui en réalité sont aux antipodes de la vraie SCIENCE, la DIVINE SCIENCE, celle synonyme de vérité! C'est cette vérité qui de nos jours est taxée de "complotisme" et j'en passe!

Kronecker avait en partie raison en disant que "Dieu a fait les nombres entiers, tout le reste est l'œuvre de l'homme". Sauf qu'il ignorait ce qui était derrière les paradigmes scientifiques dans lesquels tous travaillaient, lui comme Cantor. Et David Hilbert avait raison de dire que Cantor a créé un vrai paradis avec le paradigme de la théorie des ensembles. Sauf qu'il ignorait que les paradoxes qu'il croyait avoir résolu avec la méthodologie axiomatique qu'il proposait, n'étaient pas résolus, mais simplement se présentaient sous d'autres formes encore plus vicieuses, comme par exemple le problème de la division par zéro, qui est donc la question de l'infini, du vrai. Avec le concept d'Univers TOTAL, la théorie des ensembles et la science de manière générale trouve son vrai Paradigme (pour plus de détails voir: L'Univers TOTAL, le nouveau Paradigme de la Science)

La notion de nombre entier variable et en particulier de nombre entier variable infini est la notion clef à laquelle nous voulons aboutir dans ce document. Mais pour la comprendre, il faut bien comprendre aussi la notion de nombre entier constant ou nombre entier fini. Le présent document a juste pour but de brosser dans les grandes lignes et sans entrer dans les détails le sujet amplement traité dans le livre PDF: Générescences, Nombres entiers variables, Corps omégacyclique et Division omégacyclique par Zéro . Pour de plus amples informations, voir donc ce livre.

Les générescences, pour comprendre plus en profondeur la nature des nombres entiers

Dans les cours de mathématiques des premières classes du collège ou même avant, on commence à parler de l'ensemble des nombres entiers naturels:
N = {0, 1, 2, 3, 4, 5, 6, 7, ...}.
Dans notre langage, les expressions "nombre entier naturel" ou simplement "entier naturel", sans autre précision, désigneront par défaut les éléments de ce très classique ensemble des mathématiques.

Mais de nouvelles précisions s'imposent à présent vu que nous parlons de nombres entiers naturels variables mais aussi de nombres entiers naturels variables infinis ou simplement de nombres entiers naturels infinis, etc. Car, eh oui, un entier naturel peut maintenant être infini, et nous verrons ce que cela veut dire très exactement!

Commencez par oublier ce symbole occulte "∞" très prisé des mathématiques actuelles:

Ce symbole "∞" est en fait un FAUX infini, parce que ce n'est même pas un vrai nombre, mais juste un symbole pour indiquer qu'une certaine quantité est "aussi grande que l'on veut". Mais il existe des nombres en bonne et due forme pour dire cela, et le comble est qu'ils sont bien connus en mathématiques. Comme par exemple les nombres entiers dits "non standard" introduits par Abraham Robinson, ou encore la correction des classiques ordinaux et cardinaux infinis apportée par le génial mathématicien John Conway et qui lui a servi aussi à construire ce qu'il a appelé les nombres surréels. Dans cette structure numérique remarquable foisonne toute une infinité vertigineuse d'infinis et de zéros.

Par infini dans son sens large il faut entendre un nombre réel plus grand que tout nombre réel classique et donc que tout nombre entier naturel classique. Autrement dit, étant donnée une extension des classiques nombres réels, comme celles mentionnées précédemment ou celles proposées par votre serviteur, un nombre réel x de cette extension est dit infini si pour tout entier naturel classique n, on a: x > n.

C'est la manière très rigoureuse de dire: "aussi grand que l'on veut", mais aussi de définir la très importante notion de "nombre infiniment grand", ou comme nous le dirons aussi: "nombre indéfiniment grand", ou encore: "nombre générativement grand".

Et par zéro dans son sens large il faut entendre un nombre réel strictement positif et qui est plus petit que n'importe quel nombre réel strictement positif classique. Et donc en particulier un nombre plus petit que 1/n, où n désigne tout nombre entier naturel classique non nul. Autrement dit, un nombre réel x de cette extension est appelé un zéro si pour tout entier naturel classique non nul n (c'est-à-dire n prend pour valeurs: 1, 2, 3, 4, 5, 6, 7, ...), on a: |x| < 1/n. Et l'écriture |x| désigne la valeur absolue ou le module de |x|.

Je me souviens qu'il y a plus de 40 ans, au lycée, en classe de Terminale de série C (série mathématiques et sciences physiques), je ne supportais pas nombre d'aspect du langage des limites, du genre "x tend vers a", avec souvent l'interdiction pour x d'être exactement égal à a, notamment si cette égalité conduit à une division par 0.

Par exemple, calculer la limite de: y = (x² - 4)/(x - 2) quand x tend vers 2. La limite est 4, mais quand on veut la calculer directement en donnant à x la valeur 2 absolu, on se heurte à une division par zéro, de type 0/0.

Mais si, utilisant un infinitésimal ou infiniment petit δ (soit dit en passant ce n'est pas le logo de Tik Tok mais la lettre grecque delta minuscule...) on calcule la limite non plus pour x valant 2 absolu mais pour x valant 2+δ, un nombre 2 ayant pour sens un nombre qui tend vers 2 absolu, le résultat devient (4+δ)×δ/δ, qui est toujours une division par zéro de type 0/0 ou (4+0)×0/0, mais cette fois-ci avec un 0 relatif et non plus absolu. Et même si c'était le cas, ce n'est plus une catastrophe non plus dans le Nouveau Paradigme, à savoir l'Univers TOTAL.

Car à présent, multiplier ou diviser n'importe quel nombre x par le zéro absolu, à savoir l'omicron o, donne le zéro absolu. Mais on veut le résultat aux horizons zéros et pas nécessairement à l' horizon spécial zéro absolu. A cet horizon, le calcul (4+o)×o/o vaut exactement o. Autrement dit, la quantité y = (x² - 4)/(x - 2) pour x valant exactement 2 absolu vaut exactement o.

Mais ce qui nous intéresse est cette quantité pour x valant exactement un 2 relatif. Et là c'est (4+δ)×δ/δ ou (4+0)×0/0, où le symbole δ ou 0 désigne 0 relatif, c'est-à-dire un infinitésimal, un infiniment petit. Et là le résultat est 4+δ ou 4+0, un nombre ayant pour sens: "un nombre tendant vers 4 absolu".

J'aime nettement mieux cela, car on a exprimé une information ou une idée, ici l'idée de "tendre vers un nombre a", par un nombre mathématique précis! Et je suis simplement en train de dire que, comme pour le nombre zéro, la notion d'infini doit s'exprimer aussi par un nombre réel précis. Il n'y a aucune raison que cela ne puisse pas se faire, et que l'on utilise ce symbole vague ∞ pour dire "tend vers l'infini", comme si l'on parlait d'un nombre réel, alors que ce n'est pas le cas.

Je me souviens donc qu'au lycée, suite à un cours d'analyse sur les suites de nombres réels mais aussi sur le calcul intégral (domaine où l'on manipule particulièrement les quantités infiniment petites, les dx, les dy, les dz, et où l'on calcule des dérivés du genre: dy/dx, qui est la division de deux nombres infiniment petits, donc de deux zéros pour ainsi dire), j'ai eu un grand flash et une très forte intuition qu'il doit exister un moyen de construire une extension des nombres réels où existent ce que j'appelle maintenant des infinis et des zéros. Dans cette extension, le langage assez frustrant des limites, notamment quand une quantité x tend vers une quantité a, mais sans que x ait le droit de prendre au besoin exactement la valeur a (par exemple pour cause de division par zéro, de la non définition d'une fonction pour une valeur, etc.), doit être banni. Remplacez le "tend vers" par "égal à".

Il y a donc la construction de l'analyse non standard d'Abraham Robinson, ou celle des nombres surréels de John Conway et d'autres. Ou encore la construction que votre serviteur propose dans le livre PDF: L'Univers TOTAL et les nombres omégaréels. Mais la construction la plus fondamentale dont je traite dans tous les livres et dont il sera encore question ici, est la construction générative, qui repose sur la très fondamentale notion de générescences. Dans toutes ces extensions des classiques nombres réels, que ce soit donc celles connues dans les mathématiques traditionnelles ou celles de votre serviteur, il y a toute une infinité de zéros et d'infinis qui ne demandent qu'à être utilisés pour faire des calculs précis avec.

Je viens de donner les raisons mathématiques pour lesquelles le pseudo-nombre ∞ doit être oublié à présent, sauf évidemment si on lui donne maintenant une définition en tant que nombre précis. Mais le plus grave est qu'il sert le plus souvent à éviter de parler du VRAI infini, des VRAIS infinis!

Il existe toute une infinité de zéros, et chaque zéro a son infini associé et vice-versa. Les deux sont inverses l'un de l'autre, ce qui veut dire que diviser 1 par un zéro considéré donne comme résultat l'infini correspondant. Et à l'inverse diviser 1 par un infini considéré donne comme résultat le zéro correspondant. Déjà ceci tord le cou à l'idée que la "division par zéro" serait "impossible".

On vous dira en analyse que la limite de 1/x quand x tend vers zéro est l'infini, et que la limite de 1/x quand x tend vers l'infini est zéro. C'est le pseudo-nombre ∞ entre autres qui permet d'éviter ici un langage d'égalité, tout simplement, autrement dit, que x prenne tout simplement pour valeur le zéro ou l'infini.

La question est: pourquoi continue t-on à dire que la division par zéro serait "impossible", alors qu'on a connaissance depuis belle lurette d'extension des nombres réels qui offrent une infinité de solutions à cette opération? Jusqu'à il y a une quinzaine d'années encore (j'écris ceci en 2023) j'ignorais l'existence des extensions de nombres réels dont j'ai parlé, et moi-même j'avais déjà mis au point ma version. J'avoue avoir été content de trouver la voie de construction d'une structure numérique qui me tenait à coeur pendant 30 ans (depuis mes années de Terminale de lycée, les années 1980).

Et je fus ravis d'apprendre que des mathématiciens ont déjà proposé des constructions du même genre, et dans le même souci. Mais je fus littéralement choqué de lire dans une encyclopédie mathématique un "expert" minimiser l'importance de ces extensions des nombres réels, les reléguant au rang d'intréessantes curiosités mathématiques, mais sans grand intérêt pratique. Car, dit-il, l'unique intérêt serait juste la modification du langage mathématique, le remplacement du "tend vers" (le langage des limites donc) par le "égal à ".

Or, même rien que ceci est très loin d'être anodin! Les structures numériques classiques enrichies avec des nombres infinis et infinitésimaux changent considérablement la donne, cela simplifie énormément la pratique mathématique. Ces structures ont un potentiel infini, elles donnent toute une nouvelle compréhension de l'Univers, et j'en passe. Mais lui soutient que tout ce qu'on peut faire avec ces infinis et ces infinitésimaux (ces zéros donc) on peut le faire sans eux, ce qui est FAUX! Car si ce qu'il dit est vrai, on ne continuerait pas à dire que la division par zéro est "impossible"! Car ces structures offrent justement l'une des voies de réparation de cette grave lacune des mathématiques, qui impacte tous les domaines scientifiques et technologiques.

J'en suis venu à la conclusion que ces lacunes ne sont pas du tout des erreurs de paradigme, mais sont volontaires! Ce n'est pas qu'on ne PEUT pas diviser par zéro, mais qu'on ne VEUT pas le faire! On ne veut pas de sciences avec le VRAI Zéro (l'Alpha) et le VRAI Infini (l'Oméga), avec tous les vrais zéros et les vrais infinis correspondants, et vice-versa. On sait où conduirait une Science enfin complète (au sens courant du terme "complet", oui "TOTAL", comme "Univers TOTAL", "Réalité TOTALE", comme au sens spécifique de la complétude de Gödel), à savoir tout droit... vers DIEU l'Alpha et l'Oméga!

Je commençais à comprendre ce qui devient de plus en plus évident à l'ère du Covidisme, de l'Ukrainisme, du Climatisme, du Lgbtisme, du Transgenrisme, bref à l'heure de toutes les nouvelles religions, à savoir que même la science telle qu'elle était faite jusqu'à présent était une religion qui ne disait pas son nom, et qui est le Scientisme! Ce n'est pas la vérité scientifique absolue et universelle qui importait, mais les dogmes et la doxa d'un système! De voir que les sciences et même les mathématiques, réputées la reine des sciences, la science exacte par excellence, n'échappe pas à la règle, m'a complètement consterné, abasourdi et plongé depuis dans une indignation permanente et même une sorte de colère juste, une colère divine et une divine colère, contre ceux que je discerne de plus en plus être la cause profonde de tout cela. De nos jours, des scientifiques tout à fait honnêtes, consciencieux, qui eux aussi croyaient comme moi auparavant que le but de la science c'était la vérité et uniquement la vérité, tombent des nues!

Ici un mathématicien viré, là un physicien ou une physicienne tué(e) socialement. Et là encore un Prix Nobel de biologie qui est tout à coup accusé de "complotisme". Et là encore un infectiologique de renom vilipendé, et là encore un médecin irréprochable trainé dans la boue. Et là encore une grande généticienne démolie et qui tente de renaître de ses cendres, et j'en passe, tellement la liste devient... infinie! Et je ne parle plus des personnels soignants suspendus! Et pourquoi donc tout cela? Que se passe t-il?

Tout simplement parce que tous ces gens font tout simplement leur métier, ils pratiquent la science comme elle doit être, et comme eux l'ont toujours conçue. Ils osent remettre en question la doxa, ce qui apparaît clairement comme des dogmes religieux plus que de la science. Et le pire, c'est qu'à côté de ces nouvelles religions, même la religion classique fait figure de science! Il y a plus de vérité chez un intégriste islamiste que chez des gens qui se prétendent des incarnations de la vérité, des défenseurs de la libérté, de l'égalité, de la fraternité! C'est le monde complètement à l'envers!

Bref, pour revenir au sujet, il y a donc une quinzaine d'années, je constatais avec stupéfaction qu'une religion se cache dans la manière de faire la science jusqu'ici, et les scientifiques sincères ignoraient qu'ils servaient cette religion, ou que dis-je, cette SECTE, jusqu'à ce que les gourous leurs tapent sur les doigts et même plus que cela, juste parce qu'ils disent la vérté! Il y a donc longtemps que le pseudo-nombre ∞ n'avait plus sa place en mathématiques! Déjà en 1882, quand Georg Cantor a découvert l'existence de toute une hiérarchie de nombres infinis, les jours du pseudo-nombre ∞ devaient être comptés!

Un ordinal est tout simplement la généralisation de la notion de nombre entier naturel. Les ordinaux finis sont ce qu'on appelle les nombres entiers naturels, les éléments de N = {0, 1, 2, 3, 4, 5,  6,  7,  ...} donc.

Quand bien-même donc que la conception classique d'ordinaux et cardinaux souffre jusqu'à présent encore d'une tare qui est le problème des "ordinaux limites". C'est l'idée FAUSSE que certains ordinaux infinis n'auraient pas de prédécesseurs. Tout ordinal a un successeur, comme le disent aussi les conceptions classiques, mais c'est avec la notion de prédécesseurs qu'il y a un très gros souci. L'ordinal zéro et tous les ordinaux infinis dits "limites" n'ont pas de prédécesseur, et c'est ce qui est faux donc. Seul zéro parmi les ordinaux n'a pas de prédécesseur, mais en introduisant la notion d'ordinal relatif, même lui aussi a un prédécesseur, si bien que tous les ordinaux, finis ou infinis, ont des prédécesseurs. C'est ici que la notion d'ordinal comme notion de nombre entier naturel variable est d'une extrême importance. Car un nombre entier naturel variable, qu'il soit fini ou infini, a un successeur, et a un prédécesseur sauf s'il s'agit de zéro (et encore il est facile de donner des prédécesseurs à zéro lui aussi, avons-nous dit).

J'analyse largement le problème ailleurs, je ne m'attarde pas davantage là dessus ici. Ce sur quoi je veux maintenant brièvement attirer l'attention en passant, avant d'entrer dans le vif du sujet de ce document, c'est que le symbole classique pour représenter l'infini est tout sauf anodin:

On avance souvent que ce symbole représente la lemniscate, alors qu'en réalité son vrai sens est occulte, c'est l'Ouroboros, le Serpent qui se mort la queue, et cela nous ramène à la Genèse. Les initiés savent le vrai sens de ce symbole:

Les nombres entiers constants et les nombres entiers variables

Et maintenant donc, commençons la découverte du VRAI infini avec donc l'ensemble des nombres entiers naturels:
N = {0, 1, 2, 3, 4, 5, 6, 7, ...}.

Il s'agit d'un ensemble infini, en ce sens qu'il a une infinité d'éléments, notion d'infinité en un sens intuitif. En effet, on voit qu'après chaque élémént n il y a l'élément suivant n+1, et c'est ainsi indéfiniment. Et chaque élément est différent de tous ceux qui le précédent, s'il en existe.

En effet, il n'y a pas de nombres entiers naturels qui précèdent 0, et c'est le seul entier naturel qui n'a pas de prédécesseurs. Et si l'on s'intéressait à l'ensemble des nombres entiers relatifs: Z = {..., -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, ...}, qui contient tous les entiers naturels, qui sont positifs, mais aussi leurs opposés respectifs, qui sont dits "négatifs": ..., -7, -6, -5, -4, -3, -2, -1, 0 (et 0 étant son propre opposé), on voit que dans cet ensemble le 0 a des prédécesseurs. Mais nous ne nous intéressons ici qu'aux entiers naturels, qui sont positifs. Ils sont les nombres entiers fondamentaux, et à partir d'eux on définit non seulement les autres types de nombres entiers (les négatifs, les infinis, etc.), mais aussi tous les autres types de nombres: décimaux, rationnels, réels, complexes, etc..

Il suffit donc de comprendre les secrets des nombres entiers naturels pour comprendre vraiment les secrets de tous les nombres! Mais le problème est que les mathématiciens de base (j'entends par là à la sortie des lycées, notamment des classes spéciales de mathématiques, et ce jusqu'au premier cycle universitaire, et même jusqu'à la licence, et même encore ce qu'à mon époque on appelait la maîtrise, et qu'on appelle plus récemment les masters), oui toutes ces "têtes savantes" de base, voit généralement les nombres entiers naturels comme les nombres basiques, qui n'ont pas beaucoup de secrets pour eux, comparativement aux nombres réels par exemple, avec les mystères autour des nombres du genre pi ou π. Vous savez ce fameux nombre: 3.141592653589793238462643383...

Ils considérent donc que, à part les casse-têtes des nombres premiers, et bien d'autres casse-têtes sur les nombres entiers naturels, ceux-ci n'ont pas de grands secrets, quant à leur définition ou construction par exemple.

Par exemple, si l'on considère le chiffre romain I, et si l'on introduit (comme nous allons le faire à partir de maintenant) la lettre grecque omicron, o, pour réprésenter le zéro ou le rien, la liste des nombres entiers naturels aurait pu être tout simplement cette suite de symboles:
o, I, II, III, IIII, IIIII, IIIIII, IIIIIII, ....
Autrement dit, en considérant que le symbole I représente le fait juste de tracer un trait, sur le sable de la mer par exemple, les nombres entiers naturels consistent juste à tracer à chaque fois un trait de plus. On a ainsi théoriquement tous les nombres entiers naturels, de la manière la plus "primitive" ou la plus "enfantine" qui soit, sans même avoir besoin de savoir lire, écrire et même compter! Il suffit donc juste de savoir tracer un trait, sur le sable par exemple donc, et cela un bambin de 3 ans et même moins sait le faire! Les nombres entiers naturels, c'est aussi "simple" que ça. Et pourtant, oui et pourtant!

Cette logique simple, c'est ce que nous appelons la logique générative des nombres ou les générescences, ou encore les informations unaires:

Dans n'importe quel système de numération, ou système informationnel, pour peu que la base de la numération ou de l'information soit au moins UN, oui 1, on a obligatoirement certaines informations qui sont unaires, autrement dit certaines écritures sont des générescences. Dans le classique système décimal ou base 10, dont les dix informations élémentaires ou chiffres sont classiquement notés: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, on aura par les informations: 16, 4072, 976543210, etc., mais aussi toutes les informations: 0, 00, 000, 0000, 00000, 0000000, ..., et aussi les informations: 1, 11, 111, 1111, 11111, 111111, 1111111, ..., et aussi les informations: 2, 22, 222, 2222, 22222, 222222, 2222222, ..., etc.

Et on aura aussi par exemple: 4072, 40724072, 407240724072, 4072407240724072, ..., qui sont donc les différentes répétitions ou itérations de 4072, que nous appelons les générescences d'unit 4072. Et de manière très générale, étant donnée n'importe quelle information X, on a les générescences d'unit X ou informations unaires d'unit X, qui sont donc: X, XX, XXX, XXXX, XXXXX, XXXXXX, XXXXXXX, .... Et dans tous les cas, il s'agit de réprésentations avec X de tous les nombres entiers naturels, à par la notion de zéro. Toute la simplicité mais aussi à la fois la complexité et même la magie des nombres entiers naturels, et, au-delà, de tous les nombres, se trouve là, oui dans cette logique générative, la logique des générescences ou des informations unaires. Autrement dit, le système de numération en base UN ou 1!

Les romains ont vite remarqué cette "simplicité", et ils ont donc commencé leur numération ainsi:
I, II, III, IV, V, VI, VII, ....
Les trois premiers chiffres de cette numération sont donc ni plus ni moins des générescences ou informations unaires d'unit I. Et là les romains (mais en fait aussi d'autres peuples qui ont adopté une forme ou une autre de cette numération qu'on dirait "primitive" et pourtant si fondamentale et si complexe en réalité) se sont vite aperçu de la première difficulté avec la logique de tracer juste des traits pour représenter les nombres. Eh bien c'est que quand les nombres deviennent grands, ils deviennent longs à écrire et aussi à distinguer les uns des autres.

C'est très facile en effet de distinguer les trois premiers: I, II, III, mais les confusions commencent quand il s'agit de disinguer III et les deux suivants, donc: III, IIII, IIIII. Et courage pour distinguer par exemple les générescences correspondantes aux nombres 775, 776, 777!

D'où la nécessité d'introduire de nouveaux symboles pour représenter des paquets spéciaux d'units I, autrement dit des générescences spéciales d'unit I. Les romains ont alors choisi le symbole V pour représenter le paquet de cinq units IIIII. Et le symbole X pour représenter le paquet de dix units IIIIIIIIII, etc. et l'écriture IV s'interprète comme "cinq moins une unité", IX s'interprète comme "dix moins une unité". Et VI s'interprète comme "cinq plus une unité", XI s'interprète comme "dix plus une unité". Et VII représente "cinq plus deux unités", et XII représente "dix plus deux unités", etc.

Ces conventions facilitent déjà grandement la gestion des générescences, autrement dit les nombres entiers naturels dans leur numération la plus fondamentale, la plus naturelle, la numération unaire, de laquelle toutes les autres découlent, et même en fait tout système de nombres réels positifs! En effet, pour peu que l'on prenne conscience de la notion de nombres entiers naturels variables et de toutes ses aimables et très agréables et puissantes conséquences (ce que nous allons faire ici mais que très étrangement on ne fait pas dans les conceptions traditionnelles), la théorie des nombres réels est très simple en logique générative (la logique des générescences donc), ou en tout cas pas plus compliquée que celle des nombres entiers naturels! Car, en réalité, la théorie des nombres réels, oui la bonne théorie des nombres réels, c'est tout bonnement la théorie des générescences!

En logique générative, les générescences d'unit 0 par exemple, ne se distinguent pas dans l'absolu des générescences d'unit 1 ou I ou de n'importe quel unit X. Générativement parlant (c'est-à-dire d'un point de vue des générescences), ces quatre listes sont parfaitement équivalentes:
0, 00, 000, 0000, 00000, 0000000, ...
1, 11, 111, 1111, 11111, 111111, 1111111, ...
I, II, III, IIII, IIIII, IIIIII, IIIIIII, ...
X, XX, XXX, XXXX, XXXXX, XXXXXX, XXXXXXX, ...
Seul le symbole utisé comme unit distingue ces listes, et à part ça les raisonnements fondamentaux sont exactement les mêmes pour ces listes, ainsi que les notions fondamentales que l'on définit avec elles. Et en fait on peut tout définir avec elles, et tout ce que l'on définit avec l'une des listes, on le fait de même avec toutes les autres, ce qui veut dire que les notions fondamentales sont indépendantes de l'unit X utilisé.

Par exemple, étant donné n'importe quel unit X, et ses générescences: X, XX, XXX, XXXX, XXXXX, XXXXXX, XXXXXXX, ..., même si cet unit X représente le nombre que nous appelons le zéro et notons 0, il n'empêche que X peut toujours s'interpréter comme UN et noté 1, et donc XX peut s'interpréter comme DEUX et noté 2, et XXX peut s'interpréter comme TROIS et noté 3, et ainsi de suite. Autrement dit, la notion absolue de nombres entiers naturels, notamment non nuls: 1, 2, 3, 4, 5, 6, 7, ... est totalement indépendante de l'unit utilisé pour définir ces nombres, y compris le nombre que nous appelons le zéro et notons habituellement 0.

A partir de maintenant, les générescences: X, XX, XXX, XXXX, XXXXX, XXXXXX, XXXXXXX, ..., seront respectivement notées: 1×X, 2×X, 3×X, 4×X, 5×X, 6×X, 7×X, ..., ou simplement: 1X, 2X, 3X, 4X, 5X, 6X, 7X, .... Devant la première, X ou 1×X ou 1X, il n'y a aucune générescence. Nous matérialisons cette absence de générescence par la notation: o ou o×X ou oX, où o est appelé la générescence espace ou simplement l'espace ou le zéro absolu.

La liste des générescences d'unit X est donc:
o, X, XX, XXX, XXXX, XXXXX, XXXXXX, XXXXXXX, ...,
ou: o×X, 1×X, 2×X, 3×X, 4×X, 5×X, 6×X, 7×X, ...,
ou: oX, 1X, 2X, 3X, 4X, 5X, 6X, 7X, ....
On pose ainsi donc: oX = o×X = o.
Cela signifie l'absence de toute générescence d'unit X, quel qu'il soit, donc la présence uniquement des générescences d'unit o, qui sont donc: o, oo, ooo, oooo, ooooo, oooooo, ooooooo, ..., ou: 1×o, 2×o, 3×o, 4×o, 5×o, 6×o, 7×o, ..., qui sont toutes par définition égales à o.

On pose donc que:
-- n'importe quelle information X multipliée par o donne o;
-- n'importe quelle information X divisée par o donne o;
-- o divisé par n'importe quelle information X donne o;
-- Pour toute information X, on pose: o^X = o; donc en particulier: o^o = o;
-- Pour toute information X distincte de o, on pose: X^o = 1.

Dans toute la suite, dans les contextes où la liste: 0, 1, 2, 3, 4, 5, 6, 7, ... désigne clairement les nombres entiers naturels, le 0 impliqué est le zéro absolu, l'omicron donc.

C'est l'occasion de parler brièvement de la notion de zéro en logique générative. Il y a en fait deux notions de zéro:
--> le zéro absolu, noté o et appelé l'omicron, et qui est le zéro exprimant l'absence de toute générescence, et donc de tout unit;
--> le zéro relatif, noté 0, et qui est le rapport entre un unit X avec une générescence formée d'une infinité d'units X, comme par exemple l'infinité de référence que nous notons "X...". L'information X étant prise comme l'unité de référence et notée 1, l'information "X..." ou "1...", qui signifie que l'unit X ou 1 est répété indéfiniment, représente l'infinité de référence, qui sert à définir toute autre infinité. Dans nos travaux anciens, cette infinité est notée ω:

Mais plus récemment nous la notons plutôt v:

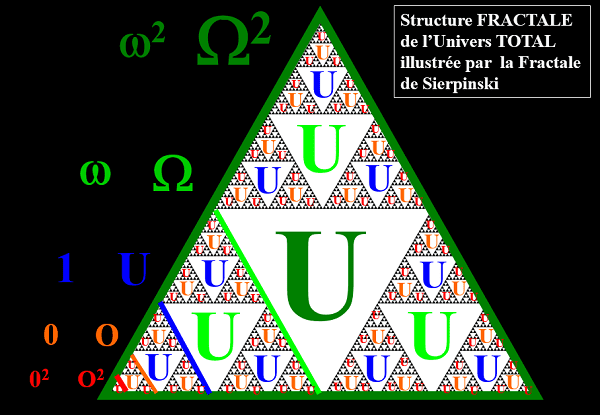
Et justement la notion de nombre entier variable et en particulier nombre entier variable infini est la notion clef que nous examinons dans ce document. Les images ci-dessus sont l'une des nombreuses manières de se représenter intuitivement ces notions.

Et maintenant, étant donné un nombre entier infini que nous noterons ω, et que nous appelerons aussi un infini relatif ou un infini génératif, on appelle le zéro associé, qualifié aussi de zéro relatif ou de zéro génératif le nombre 1/ω. Et par conséquent on a aussi: ω = 1/0. On a donc une infinité d'infinis relatifs, et donc une infinité de zéros relatifs associés. Mais on a un seul zéro absolu, qui par définition est appelé aussi l'infini absolu, et noté alors: Ω.

La notion de nombre entier naturel est une notion qu'on pense généralement bien connaître, et pourtant non. Sinon, les mathématiques ne raconteraient pas certaines graves bêtises qu'ils racontent présentement, comme par exemple l'idée que la division par zéro serait "impossible". Je reviens constamment et dans tous mes écrits sur cette question, car c'est sans doute la palme d'or des mensonges mathématiques actuels. Ou en tout cas des graves erreurs, aux graves conséquences non seulement en mathématiques, mais dans tous les autres domaines scientifiques et techniques. Vous n'avez pas idée de toutes les fois où l'on se heurte à la division par zéro, et donc où l'on raisonne avec l'idée qu'elle est "impossible", alors qu'elle est bel et bien possible.

C'est un problème de conception des nombres entiers naturels, et plus généralement des paradigmes scientifiques actuels, que je qualifie de "paradigmes de Négation", car il faut bien fonctionner avec une logique scientifique orientée vers la Négation (donc la négation d'existences, de possibilités, de réalités, etc.) pour NIER l'existence ou la possibilité de diviser par zéro. Et si l'on veut un autre exemple prouvant que les paradigmes scientifiques actuels sont faux, et conduisent à des mensonges très savants, le voici:

Par cette écriture savante, qui se lit: "La somme de tous les nombres entiers naturels n de o à l'infini ∞ est égale à -1/12", on est en train de dire qu'en additionnant tous les nombres entiers naturels, c'est-à-dire en faisant le calcul: o+1+2+3+4+5+6+7+..., on trouve à la fin (et tenez-vous bien) comme résultat: -1/12!
Oui il paraît donc que: o+1+2+3+4+5+6+7+... = -1/12

Si les choses disent vraiment ce qu'elles doivent dire, si les symboles ont réellement le sens qu'ils doivent avoir, si le signe "+" employé avec les familiers nombres entiers naturels signifie bien la familière addition et non pas quelque opération occulte, obscure pour les non initiés, ésotérique, exotique, extraterrestre, etc., si donc c'est l'addition qui est bien de chez nous, avec les nombres bien de chez nous eux aussi (je veux dire chez nous les humains créés à l'image de Dieu et non pas à l'image du Diable), alors je suis désolé de dire que ce résultat -1/12 pour la somme de tous les nombres entiers naturels est éminemment FAUX! Emminemment FAUX! C'est terrible pour une science dite "exacte", car là ce n'est pas exact du tout, hein? C'est tout sauf de l'exactitude, c'est clair:

Car en addtionnant les nombres entiers naturels n, étape par étape, cette sommation donne:
o à l'étape o,
et: o+1 = 1 à l'étape 1,
et: o+1+2 = 3 à l'étape 2,
et: o+1+2+3 = 6 à l'étape 3,
et: o+1+2+3+4 = 10 à l'étape 4,
et: o+1+2+3+4+5 = 15 à l'étape 5,
et: o+1+2+3+4+5+6 = 21 à l'étape 6,
et: o+1+2+3+4+5+6+7 = 28 à l'étape 7,
et ainsi de suite.
Et à toute étape n, la somme est: o+1+2+3+...+n = n(n+1)/2,
qui est tout simplement la formule générale, générique, générative, de cette sommation: o+1+2+3+4+5+6+7+...

Et si l'on veut maintenant comprendre, cette formule n(n+1)/2 est l'unique vrai résultat, exact, de la sommation dont nous parlons, à savoir donc la somme de tous les nombres entiers naturels! Cette formule est valable pour tout nombre entier naturel n, qu'il soit constant ou variable, fini ou infini! La clef de la question ici!

Car s'il existe des nombres entiers naturels constants, il existe aussi des nombres entiers naturels variables! Ou (et cela revient presque au même) s'il existe des nombres entiers naturels finis, il existe aussi des nombres entiers naturels infinis, qui sont des cas particuliers de nombres entiers naturels variables! Ce sont en fait les grands oubliés chaque fois que l'on parle des nombres entiers naturels.

Les nombres entiers naturels infinis (qui sont donc des cas particuliers de nombres entiers naturels variables, que nous allons voir), sont par définition des nombres entiers qui sont supérieurs à tous les nombres entiers naturels constants ou finis, c'est-à-dire les éléments de l'ensemble des nombres entiers naturels: N = {o, 1, 2, 3, 4, 5, 6, 7, ...}. Ses éléments, comme par exemple 2, ou 4, ou 7, 8692o1235473, sont tous finis ou constants. Mais N lui-même est un exemple de nombre entier INFINI! Cela on le savait.

Mais ce que l'on ignorait ou plutôt persistait à savamment ignorer, c'est que l'ensemble N, qui est donc un exemple même de nombre entier INFINI, ce qu'on appelle couramment aussi un ordinal INFINI, ici l'ordinal infini de référence, est aussi un cas particulier de nombre entier variable. Quand nous utilisons par exemple la variable n pour écrire une formule générale comme par exemple la formule n(n+1)/2, cette variable n n'est rien d'autre qu'une autre manière de parler de l'ensemble N, à savoir donc cet ensemble N mais en tant que VARIABLE n! Une autre très importante clef de l'affaire est ici.

Vous verrons par la suite comment on définit les nombres entiers variables à partir des nombres entiers constants ou finis, et comment parmi les nombres entiers variables on distingue les cas particuliers que sont les nombres entiers variables infinis ou simplement les nombres entiers infinis, ou plus simplement encore, les entiers infinis.

Pour un nombre entier variable n, ou simplement une variable n (étant entendu qu'on parle ici des nombres entiers, et donc il n'est pas nécessaire de le préciser à chaque fois; et si nous parlions des nombres réels, l'expression variable x sous-entend un nombre réel variable x), oui pour un nombre entier variable n ou variable n donc, la liste de tous les nombres entiers de o inclus à n inclus est: o, 1, 2, 3, ..., n-3, n-2, n-1, n. C'est ainsi que l'on conçoit habituellement une variable entière n. Jusque là rien de vraiment nouveau, la nouveauté vient seulement maintenant.

Et elle est similaire à la notion classique de nombre entier non standard introduite par Abraham Robinson. Sauf que lui, pour y parvenir fait appel à des axiomes techniques de logique mathématique. Alors que, comme on va le voir, aucun axiome spécial n'est nécessaire, du moment où l'on a des axiomes classiques de la théorie des ensembles, et leurs conséquences qui sont entre autres les notions d'applications ou de fonctions. Nous avons besoin notamment de la notion d'applications de N dans N, c'est-à-dire de la notion de suites d'entiers naturels.

On appelle un nombre entier variable n une applicdation de N dans N, c'est-à-dire tout simplement une suite d'entiers naturels, qu'on notera:
n = (n_o, n₁, n₂, n₃, n₄, n₅, n₆, n₇, ...).

Les indices i, qui parcourent l'ensemble N, sont appelés les rangs de la suite (terme classique du langage des suites), mais nous les appelons aussi les étapes, les instants, les moments, en employant un langage temporel, bien que les indices i soient dans l'absolu juste des entiers, ou de manière générale les générescences d'un unit X donné: oX, 1X, 2X, 3X, 4X, 5X, 6X, 7X, ..., étant distinct de o, pour que les générescences soient distinctes aussi et reviennent à dire: o, 1, 2, 3, 4, 5, 6, 7, ....

Les n_i, les éléments de la suite, sont appelés ses valeurs. L'élément n_i est la valeur prise par n au rang i ou à l'instant i. Cela signifie qu'on a un nombre entier naturel n, qui commence par prendre la valeur n_o, puis la valeur n₁, puis la valeur n₂, etc.

Plus généralement, on appelle un nombre entier variable n une applicdation de N dans Z, où Z est l'ensemble des entiers relatifs. On dit que n est un nombre entier naturel variable si à partir d'un certain rang j toutes les valeurs de n sont des entiers naturels, des éléments de N donc.

Par exemple, la suite: n = (-5, 3, 8, -2, o,7, -45, 4, 6, 8, 1o, 12, 14, 16, 18, 2o, 22, ...)
bien que prenant des valeurs négatives à certains rangs au début, ne prend par la suite pour valeurs que des entiers naturels. Cela suffit pour dire qu'il s'agit d'une suite d'entiers naturels ou un entier naturel variable.

De manière très générale, pour un nombre entier variable n, et pour toute propriété P, on dit que n vérifie la propriété P si toutes ses valeurs la vérifient à partir d'un certain rang, et pas nécessairement toutes ses valeurs, et à plus forte raison si c'est le cas. Nous dirons que n vérifie finalement P, et ce sont les propriétés finales, c'est-à-dire les propriétés à partir d'un certain rang, donc les propriétés à la fin, qui nous intéressent bien plus que les propriétés initiales, les propriétés que les valeurs ont au début.

Pour reprendre l'exemple: n = (-5, 3, 8, -2, o, 7, -45, 4, 6, 8, 1o, 12, 14, 16, 18, 2o, 22, ...), on remarque aussi qu'au début certaines valeurs sont impaires, mais que par la suite toutes sont paires. On dira pour cela que n est un nombre entier variable pair. En effet, à la fin, n reste stable sur la propriété d'avoir une valeur paire.

De même, à partir d'un certain rang, toutes les valeurs de n sont différentes de o. Donc n est (finalement) différent de o.

De la même façon, soit n'importe quelle relation binaire R définie sur les entiers naturels, et plus généralement relatifs. Et soit m et n deux entiers naturels variables. On dira que: m R n, si à partir d'un certain rang j, on a: m_j R n_j. Autrement dit, à partir d'un moment j, m est en relation R avec n. Et éventuellement m est en relation R avec n à tous les rangs.

Cette relation R peut être par exemple l'égalité "=". Si à partir d'un rang j donné la valeur de m est égale à celle de n, on dit alors que m et n sont finalement égaux. Même chose si la relation R est "<" ou ">" ou autre. Il suffit que ce soit finalement vérifié pour qu'on dise que c'est vérifié, même si donc ce n'est pas vérifié au début.

Même pour toute opération H définie sur les nombres entiers naturels et plus généralement sur les entiers relatifs. Pour deux entiers narturels variables m et n, on définit un troisième entiers naturel variable p, tel que:
(m H n)_i = (m_i H n_i).
Cela signifie que toutes les valeurs de m H n sont calculées en faisant cette opération entre valeur de rang i de m et la valeur de rang i de n.

En particulier, si H est l'addition, calculer m+n c'est additionner la valeur de rang i de m à la valeur de rang i de n. De même si l'opération H est la multiplication: on multiplie donc rang par rang. Même chose si H est l'exponentiation, ou toute autre opération: la soustraction, la division, etc. Bref, tout ce qu'on veut faire sur un nombre entier variable, sur deux nombres entiers variables, sur trois, etc., on le fait sur les valeurs, rang par rang.

Cas particuliers importants de nombres entiers variables:

--> o = (o, o, o, o, o, o, o, ...)
--> 1 = (1, 1, 1, 1, 1, 1, 1, ...), que nous appelons aussi ω_o;
--> 2 = (2, 2, 2, 2, 2, 2, 2, ...)
--> 3 = (3, 3, 3, 3, 3, 3, 3, ...)
--> etc.

Pour être plus précis encore, il y a une grande différence entre d'une part le zéro absolu o, qui est un nombre entier naturel fini ou classique, celui habituellement noté 0, et qui est le tout premier nombre entier naturel fini d'ailleurs, et d'autre part la suite de nombres entiers naturels, (o, o, o, o, o, o, o, ...), dont tous les termes, à tous les rangs donc, sont le zéro absolu o, suite que nous notons aussi [o], et qui est un nombre entier naturel variable particulier, l'un de ceux dont la variation des termes est nulle. Ici ces termes sont tous o.

Il y a donc dans l'absolu une grande différence entre o et [o], ces écritures ne désignent pas du tout le même objet mathématique, l'un étant un nombre entier naturel fini, et l'autre une application de N dans N, autrement dit une application de l'ensemble N des entiers naturels finis dans lui-même, une suite de nombres entiers naturels finis donc.

De même il y a une grande différence entre 1 et [1] = (1, 1, 1, 1, 1, 1, 1, ...), l'objet 1 étant le nombre entier naturel fini qui vient après o, et l'objet [1] ou (1, 1, 1, 1, 1, 1, 1, ...) étant lui aussi une application de N dans N, une suite de nombres entiers naturels finis donc, dont cette fois-ci tous les termes sont 1.

De même pour 2 et [2] = (2, 2, 2, 2, 2, 2, ...);
Et pour 3 et [3] = (3, 3, 3, 3, 3, 3, 3, ...), ainsi de suite;
Et de manière générale, étant donné un nombre entier naturel fini k, l'objet [k] = (k, k, k, k, k, k, k, ...) désigne l'application de N dans N, ou suite de nombres entiers naturels finis, dont tous les termes sont k.

Ceci étant précisé, par l'écriture: k = (k, k, k, k, k, k, k, ...), c'est-à-dire: k = [k], nous sommes en train de dire que dans l'ensemble N^N des suites de nombres entiers naturels finis, autrement dit les nombres entiers naturels variables, ensemble N^N dont le nombre des éléments est infiniment plus grand (oui d'un tout autre ordre de grandeur) que le nombre des éléments de l'ensemble N des nombres entiers naturels finis, les suites de nombres entiers naturels finis de la forme [k], qui sont par définition les nombres entiers naturels constants dont tous les termes sont k, jouent exactement le même rôle que k dans l'ensemble N des nombres entiers naturels finis.

A remarquer au passage qu'on peut interpréter la suite constante ou nombre entier naturel constant (k, k, k, k, k, k, k, ...) comme la générescence infinie kkkkkkk... d'unit k, c'est-à-dire ici ayant un nombre infini (au sens de "indéfini") d'units k. Dans le Nouveau Paradigme, l'Univers TOTAL, la notion d'infinité est la notion d'indéfinité, encore appelée la générité. Tous les nombres infinis sont tous les nombres indéfinis (à ne pas comprendre nombres non-définis, car ils sont définis justement, avec précision), encore appelés les nombres généris. C'est l'unique vraie notion d'infinité, l'unique Infini Oméga. Toute autre notion d'infini est dans le meilleur des cas une autre manière de parler de cet unique Infini, et dans le pire des cas une notion fausse, due au fait qu'on travaille avec une logique de Négation.

Ainsi donc, nous avons ici un même objet (k, k, k, k, k, k, k, ...), qui, vu sous un angle s'interptète comme le nombre entier naturel constant k, ou le nombre entier naturel fini k, qui est aussi l'unit de la générescence kkkkkkk..., que nous abrégeons souvent k... (à lire "k GENER"), et qui vu sous un autre angle va s'interpréter comme un nombre entier naturel infini particulier, qui est k répété indéfiniment, donc k additionné à lui-même indéfiniment. Si l'indéfinité ou l'infinité ou la générité choisie est notée ω, alors (k, k, k, k, k, k, k, ...) ou kkkkkkk... va s'interpréter comme le nombre infini ω×k. Mais ici, nous voyons pour l'instant l'objet (k, k, k, k, k, k, k, ...) ou kkkkkkk... sous son angle nombre entier naturel constant k, autrement dit on ne s'intéresse ici qu'à l'unit k de cette générescence, le nombre entier naturel qui est répété donc. .

Si l'on note [N] l'ensemble de tels nombres entiers naturels constants, [N] est une infime partie de N^N. Mais N et [N] ont exactement le même nombre d'éléments, et plus que cela ils sont juste deux manières très différentes de parler du même ensemble fondamental. Autrement dit, juste deux versions très différentes du même objet. Techniquement, on dit que N et [N] sont isomorphes. Dans le cadre de N^N, on a une version de N, qui est l'ensemble des nombres entiers naturels finis, et cette nouvelle version est donc [N], qui est l'ensemble des nombres entiers naturels constants. Cela nous permet de définir une nouvelle notion de nombre entier naturel fini, comme étant un nombre entier naturel constant, les deux notions étant désormais parfaitement synonymes.

Par contre, leurs contraires ne sont pas nécessairement synonymes, et c'est ce qui est un peu délicat. En effet, un nombre entier naturel qui n'est pas constant, c'est-à-dire qui n'est pas fini au nouveau sens de la finité est strictement variable, la précision "strictement" étant nécessaire, car au sens large de la variabilité, tous les nombres entiers naturels sont désormais tous variables! Ceux que nous qualifions de constants sont un cas particulier de variables, les éléments de [N] donc, qui est un sous-ensemble très spécial et très important de l'ensemble N^N de tous les nombres entiers naturels variables. Ce sont ces nombres entiers naturels constants qui sont les nombres entiers naturels finis au nouveau sens. Un nombre entier naturel qui n'est fini au nouveau sens est donc strictement variable. Pour éviter toute confusion, on opposera dans ce cas plutôt constant à strictement variable, étant entendu que les entiers naturels constants sont les entiers naturels finis.

Les nombres entiers naturels infinis au nouveau sens sont des cas particuliers des nombres entiers naturels strictement variables. Et le plus délicat à comprendre (ou plutôt à ne pas tomber dans une confusion) est que tous les nombres entiers naturels variables, qu'ils soient constants (autrement dit finis au nouveau sens) ou strictement variables (et éventuellement infinis au nouveau sens), sont tous FINIS au sens classique, puisque tous ne sont rien d'autre que des nombres entiers naturels classiques, donc FINIS, des éléments du bon vieil ensemble N = {o, 1, 2, 3, 4, 5, 6, 7, ...}, sauf qu'au lieu de garder tout le temps la même valeur, comme chacun des éléments de N, au lieu donc de rester sagement constants, eh bien ils varient! Ils sont donc bel et bien FINIS au sens traditionnels, mais variables.

Et maintenant, comment exprime t-on l'idée qu'ils varient? Très simple: Au lieu de ne considérer à chaque fois qu'un seul élément k de N, qui est donc fini et constant comme tous les éléments de N, on considère une suite d'éléments de N, comme par exemple donc: (16, 15, o, 3, 41, 5, 6, 725, 2, 448, 4, 4, 4, 4, 4, ...). Celle-ci est constante vers la fin, tous les termes à partir d'un certain rang sont 4, et pour cela aussi on dira qu'elle est finalement équivalente à la suite constante ou au nombre entier constant [4] = (4, 4, 4, 4, 4, 4, 4, ...).

Mais cette suite, au lieu finalement d'être constante, aurait pu aussi continuer de varier, de fluctuer entre deux valeurs par exemple: (16, 15, o, 3, 41, 5, 6, 725, 2, 448, 4, 9, 4, 9, 4, 9, 4, 9, ...). C'est l'exemple d'une suite qui n'est pas constante donc, qui est donc strictement variable, mais qui n'est pas infinie, en ce sens qu'elle ne "tend pas vers l'infini", comme on dit classiquement. Et même si elle était infinie au nouveau sens, c'est-à-dire si elle "tendait vers l'infini", il n'empêche qu'elle reste toujours FINIE au sens classique, puisque toutes les valeurs qu'elle prend sont de bons vieux nombres entiers naturels finis, autrement dit les éléments de N = {o, 1, 2, 3, 4, 5, 6, 7, ...}.

Et justement, considérons maintenant cet ensemble N. Il est la version "ensemble" de la suite: (o, 1, 2, 3, 4, 5, 6, 7, ...), que nous appelons ω₁ (lire "oméga 1" ou "oméga indice 1"), et qui est strictement variable aussi, donc un nombre entier naturel variable. Sauf qu'ici, les termes de la suite tendent vers l'infini, au sens traditionnel de l'expression, ce qui signifie que les termes finissent, à partir d'un certain rang i, par être tous plus grands que n'importe quel nombre entier naturel k fixé à l'avance. En l'occurrence ici à partir du rang i = k+1, tous les termes de ω₁ sont plus grands que k.

C'est un exemple de nombre entier naturel infini, au nouveau sens du terme "infini". Il est pourtant FINI au sens classique, puisque tous ses termes, qui sont tous des éléments de N, sont FINIS au sens classique. Et même s'il y avait des termes infinis, du moment où à partir d'un certain rang i tous les termes sont FINIS, nous dirons qu'il s'agit d'un nombre entier naturel variable FINI, car c'est ce qui se passe vers la fin qui compte.

Ce que nous venons de voir signifie que, vu sous un certain angle, le bon vieil ensemble N des nombres entiers naturels est lui-même un nombre entier naturel, FINI au sens classique, mais FINI au nouveau sens. Cette double nature FINIE-INFINIE de certains nombres entiers naturels variables, et le fait que de toutes les façons tous sont FINIS au sens classique, est d'une importance capitale, d'une puissance phénoménale! Cela permet entre autres de calculer avec des NOMBRES INFINIS exactement comme on calcule avec les NOMBRES FINIS. Cela résout beaucoup de problèmes habituellement associés à la notion d'INFINI, la division par zéro étant l'un de ces problèmes.

Bref, la notion de nombres entiers naturels variables fait une véritable jonction ou union ou unification de la notion de FINI et celle d'INFINI, comme si l'on disait que les finis et mortels et les dieux ou anges qui sont infinis et immortels, se rejoignaient ou se réconciliaient. Autrement dit, les humains retrouvent de la meilleure des manières leur divinité ou infinité perdue (Genèse 3: 1-24), ils retournent au paradis perdu (Apocalypse 21: 1-7).

Enfin... pas tous, hélas, ou en tout cas pas pour l'instant, mais ceux qui se répentent de leur Négation, et sont prêts pour la rencontre de nouveau avec DIEU. Car certains ont choisi d'aller si loin de Dieu, de s'enfoncer si loin dans leur Négation, que c'est à travers le feu purificateur de l'Enfer (Apocalupse 19: 11-21; 20: 1-15; 21: 8), oui c'est après donc un grand RESET, qu'ils seront enfin prêts à revoir le visage de Dieu. Mais alors là un très grand RESET et très grand RECYCLAGE, dans leur cas, car leur cas est grave, très grave... Je parle de ceux dans la partie basse de l'image suivante:

C'est tout cela qui se cache donc derrière ces notions mathématiques, derrière cette nouvelle science, la Science de l'Univers TOTAL, la Science de Dieu.

Etant donné donc n'importe quel nombre entier naturel clasique k, on a:
--> k = (k, k, k, k, k, k, k, ...), assimilation donc du nombre entier naturel fini k avec le nombre entier naturel constant k.
Et plus généralement toute suite dont les valeurs sont k à partir d'un certain rang ou à un moment, comme par exemple (6, 9, 1, 5, o, 17, k, k, k, k, k, k, ...), est une nouvelle définition de l'entier naturel k. La suite de référence, qui représente toutes celles qui définissent k, est donc [k], la suite qui prend tout le temps la valeur k. Ceci se généralise au cas où k est lui-même un nombre entier infini. Et plus généralement encore, la notion de nombre entier naturel variable se généralise par celle de nombre entier variable, qui peut prendre pour valeurs des nombres entiers naturels variables. On a ainsi tous les nombres entiers variables de second ordre. Puis tous les nombres entiers variables d'ordre 3, qui prennent pour valeur les nombres entiers variables d'ordre 2, et ainsi de suite. .

On continue les cas particuliers de nombres entiers naturels variables (les nombres entiers variables du premier ordre donc, ceux qui prennent pour valeurs les nombres entiers naturels classiques). On a déjà parlé de celui-ci:

--> ω₁ = (o, 1, 2, 3, 4, 5, 6, 7, ...);
comme déjà dit, cette suite est la version "suite" de l'ensemble N des nombres entiers naturels. Nous la notons souvent aussi v et l'appelons varid. Mais v, mais aussi w et ω dont nous reparlerons, sont de manière générale des variables liées entre elles par une logique qu'on verra.

Tout nombre entier variable n qui, à partir d'un certain rang prend les mêmes valeurs que v, est (finalement) égal à v.
Comme par exemple: n = (56, 17, o, 32, 4, 5, 6, 7, ...) = v.

On a:
v-1 = (-1, o, 1, 2, 3, 4, 5, 6, 7, ...);
v-2 = (-2,-1, o, 1, 2, 3, 4, 5, 6, ...);
v-3 = (-3, -2,-1, o, 1, 2, 3, 4, 5, ...);
etc.
La suite v-k, pour tout entier naturel k, s'obtient donc en faisant:
(o, 1, 2, 3, 4, 5, 6, 7, ...) - (k, k, k, k, k, k, k, ...)
= (o-k, 1-k, 2-k, 3-k, 4-k, 5-k, 6-k, 7-k, ...)
Les valeurs au début seront négatives, jusqu'au rang k où la valeur est o, puis, 1, 2, 3, etc.

A partir de v, on définit aussi les nombres 2v, 3v, 4v, 5v, etc.
Par exemple, 2v s'obtient en faisant:
(2, 2, 2, 2, 2, 2, 2, ...) × (o, 1, 2, 3, 4, 5, 6, 7, ...)
= (2×o, 2×1, 2×2, 2×3, 2×4, 2×5, 2×6, 2×7, ...)
= (o, 2, 4, 6, 8, 10, 12, 14, ...).

De même on calcule: v², v³, v⁴, v⁵, etc.
Et on a v^v, nombre que nous appelons w ou ω₂;.
Et ensuite on a w^w, nombre que nous appelons ω₃, et qui est celui que nous notons souvent simplement ω.
Et de manière générale, pour tout entier naturel k non nul, constant ou variable, on a:
ω_k+1 = ω_k ^ ω_k.

Les nombres entiers ω_k sont tous infinis, au nouveau sens de l'infinité, ou indéfinité ou générité. Nous les appelons les infinis énitiens, et il leur correspond les zéros dits énitiens aussi, les 0_k, appelés aussi les infinis onitiens, et par abus les zéros onitiens.

C'est ici qu'interviennent les trois variables spéciales v, w et ω. Par défaut, nous donnons souvent pour ω la valeur ω₃, et alors w a pour valeur ω₂, et v a pour valeur ω₁. Etant entendu que ω_o = 1.

Les infinis et les zéros énitiens sont d'importance capitale. Ils permettent de définir tous les autres infinis et zéros. .

Avec ces définitions générales de base, on peut déjà déduire beaucoup de choses très importantes, qui permettent de voir la très grande puissance de la notion de nombre entier naturel variable.

Un nombre entier naturel variable n est dit infini s'il est supérieur à tout nombre entier fini. Autrement dit, pour tout entier naturel fini k, il existe un certain rang à partir duquel toutes les valeurs de n sont supérieures à k.

Par exemple, v et tous les nombres de la forme v-k ou v+k sont infinis .

Pour tout nombre entier variable n ou variable n donc, la liste de tous les nombres entiers de 0 inclus à n inclus est donc: 0, 1, 2, 3, ..., n-3, n-2, n-1, n.

Il est clair que si n est fini ou constant, la longueur de cette liste, qui est n+1, est finie ou constante aussi. Par exemple, si n vaut 5, cette liste sera: 0, 1, 2, 3, 4, 5.

Mais si n est infini, c'est-à-dire si n "tend vers l'infini", comme on le dirait classiquement, la longueur de la liste: 0, 1, 2, 3, ..., n-3, n-2, n-1, n, tend elle aussi vers l'infini, donc est infinie au nouveau du terme. Et on a dit que par définition n est supérieur à tous les nombres entiers constants ou finis, ce qui se traduit dans cette liste: 0, 1, 2, 3, ..., n-3, n-2, n-1, n, par le fait qu'on a tous les nombres entiers finis: 0, 1, 2, 3, 4, 5, 6, 7, ..., suivis de nombres entiers infinis: ..., n-7, n-6, n-5, n-4, n-3, n-2, n-1, n.

Par conséquent, et pour revenir à la question de la sommation des nombres entiers naturels: 0+1+2+3+4+5+6+7+..., il s'agit en fait toujours d'une partie de la sommation de tous les entiers naturels de 0 à un nombre entier infini n, cette sommation qui vaut donc exactement n(n+1)/2. Mais il est très clair aussi que cette même sommation: 0+1+2+3+4+5+6+7+... peut être vue comme la sommation de tous les nombres entiers naturels de 0 à un certain nombre entier naturel variable n qui "tend vers l'infini" comme on le dirait traditonnellement. Par conséquent, cette sommation vaut toujours: n(n+1)/2, peu importe la valeur courante de n. Dans tous les cas donc, cette formule est le résultat exact de la sommation: 0+1+2+3+4+5+6+7+..., quand les nombres entiers naturels sont conçus dans la bonne logique numérique qui est la leur, à savoir ici la logique des nombres entiers variables.

Comme déjà dit, cette notion, qui est plus simple, plus riche et plus profonde que la notion similaire de "nombres entiers non standard" des paradigmes classiques, est la grande oubliée ou la savamment oubliée des paradigmes traditionnels. Et du coup les raisonnements que l'on fait sur les nombres entiers naturels et qui implique leur infinité sont généralement FAUX, comme précisément quand on affirme que:
0+1+2+3+4+5+6+7+... = -1/12

Quand on ajoute ceci à la question de la division par zéro, comme par exemple la simple division 1/0 qu'on nous dit être "impossible", c'est la preuve que les mathématiques de ce monde ne savent pas vraiment encore ce que sont les nombres entiers naturels! Sûr et certain!